Логический сигнал.

Цифровые сигналы отражают числовые значения физических величин — напряжение, температуру, механическое усилие и др. При измерении неэлектрических величин последние преобразуются в электрические, которые затем подаются на вход АЦП для получения цифровых сигналов.

Наряду с ними в цифровых устройствах действуют сигналы, появление которых связано с наступлением или ненаступлением какого-либо события. Такие сигналы тоже являются двоичными, т. е. представляются двумя уровнями потенциала — высоким (U¹) и низким (U⁰), либо наличием и отсутствием импульса. Один из этих уровней кодируется (представляется) логической единицей, а другой — логическим нулем. Наличие или отсутствие описанных сигналов и порождающие их условия связаны выражениями типа «если..., то...» и другими логическими связями. Поэтому такие сигналы называют логическими.

Задание 1.6

Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (интенсивности или ложности\\\0 и логических операций над ними.

Задание 1.7

В алгебре логики в случае одной переменной х действуют следующие правила (аксиомы):

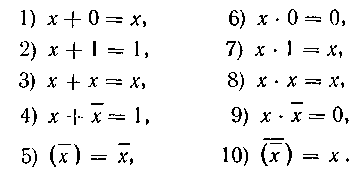(2.1)

Правила 1-4 характеризуют операцию логического сложения (дизъюнкции), правила 6-9 — операцию логического умножения (конъюнкции) и правила 5,10 — операцию инверсии. Знак логического сложения «+» читается ИЛИ (например, правило 1: «х или 0 равен х»). Знак логического умножения «•» читается И (например, «х и 0 равен 0»).

Правила 1-4, 6-9 поясняются схемами (рис. 2.2 а - з) на двух ключах в соответствии с числом слагаемых (сомножителей) в соотношениях.

Рис. 2.2. Схемы, иллюстрирующие операции логического сложения (а-г) и логического умножения (д-з)

Положению «Ключ включен» соответствует состояние «1», а положению «Ключ выключен» — состояние «0». Для логического сложения (правила 1-4) ключи в схемах соединены параллельно. Уровень высокого напряжения на выходе (F = 1) будет иметь место, если хотя бы один ключ находится в состоянии «1». Результат суммы в правилах 1, 3 зависит от значения х (при x =1, F= 1, при х =0 F = 0. Для логического умножения ключи соединены последовательно. Уровень высокого напряжения на выходе (F = 1) будет только в том случае, если оба сомножителя равны единице (оба ключа включены). В противном случае результат умножения равен нулю. Результат умножения в правилах 7,8 зависит от значения х.

Задание 1.8

Переместительный закон (закон коммутативности) для логического сложения и умножения:

Сочетательный закон (закон ассоциативности) для логического сложения и умножения:

Распределительный закон (закон дистрибутивности логического умножения по отношению к сложению):

х (у +z) = ху + хz.

Для многих случаев алгебраических преобразований полезными являются тождества, относящиеся к двум и трем переменным:

Выражения 2) и 3) называют законом поглощения; 1),5) – законом склеивания.

В справедливости тождеств 1 и 2 нетрудно убедиться, вынося за скобку в левой части переменную х. Тождество 3 доказывается с помощью распределительного закона х(х + у) = хх + ху = х + ху = х. Аналогично доказывается и тождество 4. Для доказательства тождества 5 раскроем скобки в левой части:

(х + у)(х + z) = х + хz + ху + уz= х + ху + уz = х + уz.

К основным законам алгебры логики относятся законы инверсии для логических сложения и умножения (теоремы де Моргана):

т.е. инверсия суммы переменных есть произведение их инверсий;

т.е. инверсия произведения переменных есть сумма их инверсий.

В общем случае теоремы де Моргана могут быть представлены в виде, предложенном Шенноном:

Теорема в таком виде утверждает, что инверсия любой функции получается заменой каждой переменной ее инверсией и одновременно взаимной заменой символов сложения и умножения. При практическом применении теоремы необходимо строго соблюдать группировки членов, выраженные как явными, так и неявными скобками. В качестве примера определим инверсию функции F = ху + ху. По правилу (2.8) находим:

Задание 1.9

Дизъюнктивная нормальная форма (ДНФ)- представляет собой логическую сумму элементарных конъюнкций (минтермов). Сумма произведений переменных.

Конъюнктивная нормальная форма (КНФ)- представляет собой логическое произведение элементарных дизъюнкций (макстермов). Произведение сумм.

Минтерм (конституента единица конъюнкция, которая связывает только отдельные переменные в прямом или инверсном виде.

Макстерм (конституента нуля)- дизъюнкция, которая связывает отдельные переменные в прямом или инверсном виде.

Задание 1.10

таблицей истинности – это таблица, описывающая логическую функцию, в которой для каждой комбинации значений переменных указывается значение функции. Таким образом, таблица истинности определяет алгоритм работы создаваемой цифровой схемы. От табличного представления функции переходят к аналитической записи ее в СДНФ или СКНФ.

СКНФ – совершенной конъюнктивной нормальной форме

СДНФ - совершенной дизъюнктивной нормальной форме

Таблица истинности

Номер комбинации	X	Y	Z	F

Задание 1.11

Минимизацией н азывают процедуру упрощения логической функции для того, чтобы она содержала минимальное количество членов при минимальном числе переменных. В простых случаях минимизацию можно осуществить, непосредственно используя основные законы булевой алгебры.

Используя закон склеивания для первого и третьего членов, и для второго и четвертого, а также одно из тождеств алгебры логики получим:

=

= .

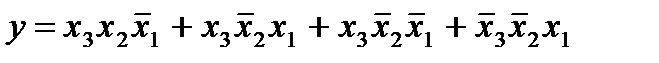Полученное выражение равносильно исходному, но намного проще его.

Задание 1.12

Карта Карно построена так, что в ее соседние клетки попадают смежные члены функции — члены, отличающиеся значением одной переменной: в один член эта переменная входит в прямой форме, а в другой — в инверсной. Благодаря этому получается наглядное представление о различных вариантах склеивания смежных членов. В карте Карно содержится столько клеток, сколько комбинаций (наборов) можно составить из прямых и инверсных значений n переменных по n членов в каждой. Так, при n=2 карта содержит четыре клетки (рис.2.4,а), при n= 3 — восемь клеток (рис.2.4,б), при n= 4 - 16 клеток (рис.2.4,в).

Каждая клетка соответствует определенной комбинации переменных. Так, например, левая верхняя клетка карты (см. рис.2.4,а) соответствует комбинации xy,: над столбцом левых клеток указан х, в прямой форме, возле верхней строки записан в прямой форме y. Наборы переменных, на которых F = 1 (в дальнейшем логическую функцию будем обозначать y), т.е. минтермы функции, отмечаются в соответствующих клетках карты 1, в остальные клетки записываются 0 или их оставляют пустыми.

Рис.2.4. Карта Карно функции для двух (а), трех (б) и четырех (в)

переменных

Две стоящие в соседних клетках 1 свидетельствуют о том, что в составе СДНФ имеются члены, отличающиеся значением одной переменной. Такие члены, как известно, склеиваются. Склеивание каждой пары минтермов уменьшает число входящих в них переменных на 1.

Задание 2.

Задание 2.1

52:2=26 0 1101002

26:2=13 0

13:2=6 1

6:2=3 0

3:2=1 1

52₁₀=1*2⁵+1*2⁴+0*2³+0*2²+0*2¹+0*2⁰=110100₂

Задание 2.2

101011₂ = 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 0 × 2¹ + 1 × 2¹ + 1 × 2⁰ = 32 + 8 + 2 + 1 = 43₁₀

Задание 2.3

110110₂+1011₂=1000001₂

+ 1011

Задание 2.4

1110₂-1010₂=100₂

-1010

Задание 2.5

1111₂*101₂=1001011₂

* 101

0

1111

Задание 2.6

25₁₀=1*2⁴+1*2³+0*2²+0*2¹+1*2⁰=11001₂

25:2=12 1 11001 ₂

12:2=6 0

6:2=3 0

3:2= 1 1

32₁₀= 1*2⁴+1*2³+0*2²+0*2¹+1*2⁰=110100₂

32:2=16 0 100000₂

16:2=8 0

8:2=4 0

4:2=2 0

2:2=1 0

11001₂/100000₂=0,11001₂

Задание 2.7

Ƴ = X₃ X₂X₁ + X₃ X₂ X₁ + X₃ X₂ X₁ + X₃ X₂ X₁ =

X₃ X₂ (X₁ + X₁) + X₃ X₁ (X₂ + X₂) = X₃ X₂ + X₃ X₁

Дата добавления: 2017-02-01