
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Собственная проводимость полупроводников
Полупроводниками называют класс веществ (твердых тел), у которых полностью занята электронами валентная зона, отделенная от зоны проводимости узкой (порядка 1 эВ) запрещенной зоной. Их электропроводность меньше электропроводности металлов, но больше электропроводности диэлектриков.
К полупроводникам относятся элементы (Si, Ge, As, Se, Te), химические соединения (оксиды, сульфиды, селениды), сплавы элементов различных групп.
Основным признаком, выделяющим полупроводники как особый класс веществ, является сильное влияние температуры и концентрации примесей на их электрическую проводимость.
Различают собственные и примесные полупроводники. Электропроводность чистых полупроводников (в которых совершенно отсутствуют примеси) называют собственной проводимостью.
К собственным полупроводникам относятся германий и кремний. Молекулярная структура кремния представлена на рис. 8.8, где:
 - ядро и внутренние электронные оболочки;
- ядро и внутренние электронные оболочки;
 - дырка, вакансия с отсутствующей связью;
- дырка, вакансия с отсутствующей связью;
 - валентные электроны, образующие ковалентную связь.
- валентные электроны, образующие ковалентную связь.
 У германия и кремния – одинаковая кристаллическая решетка: каждый атом окружен четырьмя атомами, находящимися в вершинах правильного тетраэдра. На наружной оболочке атома имеется по четыре валентных электрона, поэтому каждый атом образует четыре ковалентных связи с четырьмя ближайшими от него соседями.
У германия и кремния – одинаковая кристаллическая решетка: каждый атом окружен четырьмя атомами, находящимися в вершинах правильного тетраэдра. На наружной оболочке атома имеется по четыре валентных электрона, поэтому каждый атом образует четыре ковалентных связи с четырьмя ближайшими от него соседями.




 На рис. 8.9 показана энергетическая структура электронов в полупроводнике. При Т=0 все уровни валентной зоны заняты, а уровень Ферми лежит в запрещенной зоне, отделяющей зону проводимости. При этом в зоне проводимости электронов нет. Для полупроводников характерно, что ширина запрещенной зоны составляет до 10 кТ. При комнатных температурах ²размытость² функции Ферми-Дирака перекрывает
На рис. 8.9 показана энергетическая структура электронов в полупроводнике. При Т=0 все уровни валентной зоны заняты, а уровень Ферми лежит в запрещенной зоне, отделяющей зону проводимости. При этом в зоне проводимости электронов нет. Для полупроводников характерно, что ширина запрещенной зоны составляет до 10 кТ. При комнатных температурах ²размытость² функции Ферми-Дирака перекрывает  , и вероятность перехода электронов валентной зоны в зону проводимости не равна 0.
, и вероятность перехода электронов валентной зоны в зону проводимости не равна 0.
Таким образом, в полупроводниках (что их коренным образом отличает от диэлектриков) сравнительно небольшие энергетические воздействия, обусловленные нагревом или облучением, могут привести к отрыву некоторых электронов от своих атомов. В этом состоит механизм образования носителей в чистых полупроводниках.
При температуре T=0 K и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении температуры электроны с верхних уровней валентной зоны могут перейти на нижние уровни зоны проводимости. При наложении электрического поля электроны перемешаются против поля. В полупроводнике появляется электрический ток. Проводимость собственных полупроводников, обусловленная электронами, называется электронной проводимостью, или проводимостью n - типа.
Из-за теплового перехода электронов в валентной зоне возникают вакантные состояния, получившие название дырок. Во внешнем электрическом поле на освободившееся от электрона место, дырку, может перейти электрон с соседнего уровня, а дырка появится в том месте, которое покинул электрон и т.д. Такой процесс заполнения дырок электронами равноценен перемещению дырки в направлении, противоположном перемещению электрона. В действительности дырки не перемещаются. Проводимость собственных полупроводников, обусловленная дырками (квазичастицами), называется дырочной проводимостью, или проводимостью p - типа.
Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне. Следовательно, если концентрация электронов проводимости и дырок равна соответственно ne и np, то ne = np.
Проводимость собственных полупроводников всегда является возбужденной, т.е. появляется только под действием внешних факторов (повышения температуры, облучения, сильных электрических полей и т.д.).
В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны. При переходе электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачивается энергия активации, равная ширине запрещенной зоны E, что приводит к появлению в валентной зоне дырки. Энергия, затраченная на возникновение пары носителей тока, должна делится на две равные части. Следовательно, начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от которой возникает возбуждение электронов и дырок.
В физике твердого тела доказывается, что концентрация электронов в зоне проводимости
 , (8.17)
, (8.17)
где W2 – энергия, соответствующая дну зоны проводимости;
WF – энергия Ферми;
T – термодинамическая температура;
C1 – постоянная, зависящая от температуры и эффективной массы электрона проводимости.
Примечание. Эффективная масса – величина, имеющая размерность массы. Она характеризует динамические свойства электронов проводимости и дырок. Позволяет учитывать действие на электроны проводимости не только внешнего поля, но и внутреннего периодического поля кристалла, рассматривать их движение во внешнем поле как движение свободных частиц, не учитывая взаимодействие электронов проводимости с решеткой.
Концентрация дырок в валентной зоне
 , (8.18)
, (8.18)
где C2 – постоянная, зависящая от температуры и эффективной массы дырок;
W1 – энергия, соответствующая верхней границе валентной зоны. Энергия возбуждения в данном случае отсчитывается вниз от уровня Ферми, поэтому величины в экспоненциальном множителе разные.
Согласно тому что ne = np, имеем
 . (8.19)
. (8.19)
Если эффективные массы электронов и дырок равны, то при данной температуре C1=C2 и, следовательно,
 .
.
Откуда
 . (8.20)
. (8.20)
Таким образом, уровень Ферми в собственном полупроводнике действительно расположен в середине запрещенной зоны.
Так как для собственных полупроводников DW>>kT, то распределение Ферми-Дирака имеет вид
 , (8.21)
, (8.21)
где <Ni> – среднее число фермионов в состоянии с энергией Wi;
m – химический потенциал.
При данных условиях распределение Ферми-Дирака переходит в распределение Максвелла-Больцмана:
 , (8.22)
, (8.22)
где  .
.
Таким образом, имеем:
 . (8.23)
. (8.23)
Заменив в формуле (8.23) (W - WF) = DW/2, получим
 . (8.24)
. (8.24)
Так как количество электронов, перешедших в зону проводимости, а следовательно, и количество образовавшихся дырок пропорционально <N(W)>, то удельная проводимость собственных полупроводников
 , (8.25)
, (8.25)
где go – постоянная, характерная для данного полупроводника.
Удельное электросопротивление полупроводников
 . (8.26)
. (8.26)
Увеличение проводимости полупроводников с повышением температуры объясняется тем, что с повышением температуры у полупроводников растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости.
В полупроводниках, помимо процесса генерации электронов и дырок, возможен процесс их рекомбинации. Электроны могут переходить из зоны проводимости в валентную зону, отдавая решетке избыточную энергию, испуская кванты электромагнитного излучения. В результате для каждой температуры устанавливается определенное равновесие концентрации электронов и дырок, зависящее от температуры.
Скорость рекомбинации, т.е. число исчезающих в единицу времени электронно-дырочных пар, определяется свойствами полупроводника; кроме того, она пропорциональна концентрации электронов и дырок, так как чем больше число носителей заряда, тем вероятнее их встреча, завершающаяся рекомбинацией. Таким образом, скорость рекомбинации
 . (8.27)
. (8.27)
Но число дырок в идеальной кристаллической решетке собственного полупроводника равно числу свободных электронов  . Поэтому
. Поэтому
 , (8.28)
, (8.28)
где  – коэффициент рекомбинации, определяемый свойствами полупроводника.
– коэффициент рекомбинации, определяемый свойствами полупроводника.
Скорость генерации (число освобождающихся в единицу времени электронно-дырочных пар) зависит от температуры полупроводника и ширины его запрещенной зоны.
В стационарном режиме существует динамическое равновесие: скорость генерации равна скорости рекомбинации, отсюда
 или
или 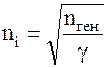 . (8.29).
. (8.29).
По формуле (8.29) можно определить число свободных электронов в полупроводнике. Так, например, при комнатной температуре число свободных электронов в германии  , в кремнии –
, в кремнии –  .
.
|
|
Дата добавления: 2017-02-01; Просмотров: 58; Нарушение авторских прав?; Мы поможем в написании вашей работы!