Потоки в сетях. Теорема Форда-Фалкерсона о максимальном потоке

Пусть G=(V,A) - взвешенный ориентированный (n,m) граф и R= 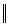r(i,j) 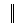- его матрица весов, элемент которой r(i,j) - вес дуги (i,j), (i,j) A. Пусть в графе G нет петель и контуров. Выделим в нём две особые вершины - вершину “исток” (u) и вершину “сток” (s). Вершины графа G мы будем интерпретировать как географические пункты, дуги - дороги их соединяющие, веса дуг - пропускные способности дорог, т.е. количество груза которое можно перевезти по дороге в единицу времени. Таким образом, построенную сетевую модель называют транспортной сетью. Задача поиска максимального потока в транспортной сети заключается в определении максимально возможного объема груза, который может быть перевезен из истока в сток по существующим дорогам с заданными пропускными способностями.

Математическая модель.

В качестве неизвестных математической модели выберем nn матрицу X= 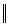x(i,j) 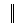, элемент которой x(i,j) - означает количество груза, которое в единицу времени будет перевезено из пункта i в пункт j, (i,j) A

Ограничения математической модели.

x(i,j) 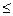r(i,j), (i,j) A. (1)

По дороге (i,j) нельзя перевозить груза больше, чем пропускная способность дороги.

x(i,j) = - x(j,i), (i,j) A. (2)

Количество груза, перевезенное из пункта i в пункт j равен количеству груза с обратным знаком, которое будет перевезено в обратном направлении.

x(i,j)= 0, если i=j, (i,j) A. (3)

Внутри промежуточных пунктов груз не перевозится.

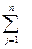x(i,j) = 0, если i V\ {u,s}. (4)

В промежуточных пунктах груз не пропадает.

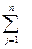x(u,j) 0. (5)

Из истока отправляется неотрицательное количество груза.

Матрица X, удовлетворяющая условиям (1) -(5), называется потоком в транспортной сети.

Постановка оптимизационной задачи.

В качестве критерия оптимальности выберем функционал

F(X) = 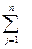x(u,j) 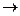max. (6)

Критерий (6) означает максимизацию величины груза, который может быть перевезен по транспортной сети.

Полученная задача (1) -(6) поиска максимального потока в транспортной сети является задачей линейного программирования. Её решение может быть осуществлено, например, симплекс-методом. Однако специфика задачи позволила для её решения построить более эффективный метод, основанный на теореме Форда-Фалкерсона.

В дальнейшем будем называть величину F(X) - мощностью потока X. Поток X(0), на котором достигается оптимальное решение задачи (1) -(6), называется максимальным потоком.

Назовем (S(u),S(s))- сечением сети, если пара множеств S(u) и S(s) является разбиением множества вершин V, при котором u S(u), s S(s).

Обозначим через Q(S(u), S(s)) = x(i,j) - величину потока через сечение (S(u),S(s)), здесь суммирование происходит, соответственно, по всем вершинам множества S(u) и всем вершинам множества S(s).

Обозначим через K(S(u), S(s)) = r(i,j) - пропускную способность сечения (S(u),S(s)), здесь суммирование происходит, соответственно, по всем вершинам множества S(u) и всем вершинам множества S(s).

Дата добавления: 2017-02-01