
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Процессы осаждения
|
|
|
|
Задачи
Примеры
Пример 1.1.1. Холодильник состоит из n труб внутренним диаметром d. В трубное пространство холодильника поступает жидкость по трубопроводу, внутренний диаметр которого D. Скорость жидкости в трубопроводе W1. Определить скорость жидкости в трубах холодильника и массовый расход этой жидкости при температуре t.
РЕШЕНИЕ
Воспользуемся уравнением неразрывности (постоянства расхода) для несжимаемой жидкости:
| V = W1 . S1 = W2 . S2 = W . S, | (1.4) |
где V – объемный расход жидкости, м3/с;
W – средняя скорость потока, м/с;
S – площадь поперечного сечения потока, м2.
Следует обратить внимание, что жидкость из трубопровода заполняет n труб холодильника.
Для трубопровода круглого сечения  .
.
Скорость в трубах холодильника может быть определена:
 .
.
Массовый расход жидкости или газа G [кг/с]:
| G = V . ρ = W . S . ρ, | (1.5) |
где ρ – плотность жидкости или газа, кг/м3.
Для данной жидкости плотность может быть определена в зависимости от температуры t (таблица 1).
Пример 1.1.2. В открытом резервуаре находится жидкость с относительной плотностью Δ. Манометр, присоединенный в некоторой точке к стенке резервуара показывает избыточное давление Ризб. На какой высоте над данной точкой находится уровень жидкости в резервуаре?
РЕШЕНИЕ
Воспользуемся уравнением Паскаля:
| Р = Ро + ρ . g . h, | (1.6) |
где Р – гидростатическое давление на глубине h [м] от поверхности жидкости, Па;
Ро – давление на поверхности жидкости, Па.
И тогда  .
.
Следует иметь ввиду, что дана относительная плотность Δ:
| Δ = ρ / ρв, | (1.7) |
где ρ – плотность жидкости, кг/м3;
ρв – плотность воды, с достаточной для технических расчетов принимаем ρв = 1000 кг/м3.
Манометр показывает избыточное давление.
Абсолютное давление Р может быть найдено: Р = Ризб + Ратм, (здесь Ратм – атмосферное давление).
Пример 1.1.3. Определить режим течения жидкости в кольцевом пространстве теплообменника типа "труба в трубе" при температуре t, расход жидкости G. Наружная труба имеет наружный диаметр Dн, внутренний – Dв; внутренняя труба – dн и dв.
РЕШЕНИЕ
Для определения режима движения жидкости необходимо рассчитать критерий Рейнольдса Re:
 , ,
| (1.8) |
где W – средняя скорость потока, м/с;
dэ – эквивалентный диаметр, м;
ρ – плотность жидкости, кг/м3;
μ – динамический коэффициент вязкости, Па . с.
ρ определяется из таблицы 1, μ – из таблицы 2 или рис. 1.
Средняя скорость жидкости: 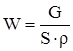 .
.
Площадь поперечного сечения кольцевого пространства
S = 0,785 . (Dв2 – dн2).
Эквивалентный диаметр может быть определен
 , ,
| (1.9) |
где S – площадь поперечного сечения потока, м2;
П – смоченный периметр, м.
Эквивалентный диаметр кольцевого сечения по формуле (1.9):
 .
.
Для потоков, проходящих по прямым трубам, характерны следующие значения критерия Рейнольдса:
Ламинарное течение Re < 2300
Переходная область 2300 < Re < 10000
Турбулентное течение Re > 10000.
Пример 1.1.4. По трубопроводу внутренним диаметром d и длиной l передается газ в количестве G. Среднее давление в сети Р, температура газа t °С. Определить потери давления на трение, приняв шероховатость стенок трубопровода е.
РЕШЕНИЕ
Потери давления на трение в прямых трубах и каналах определяется по формуле:
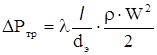 , ,
| (1.10) |
где λ – коэффициент трения;
dэ – эквивалентный диаметр, м (для трубы круглого сечения dэ равно внутреннему диаметру трубы);
l – длина трубы, м;
W – скорость потока, м/с;
ρ – плотность жидкости или газа, кг/м3.
Для гладких труб (стеклянные, медные) коэффициент λ зависит от режима течения:
для ламинарного –  , ,
| (1.11) |
для турбулентного – 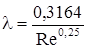 . .
| (1.12) |
При турбулентном потоке коэффициент трения зависит не только от характера движения жидкости (значения Re), но и от шероховатости стенок труб, т.е. λ = f (Re,  ), где е – средняя высота выступов шероховатости на внутренней поверхности труб, м. Зависимость коэффициента сопротивления λ от режима течения (Re) и
), где е – средняя высота выступов шероховатости на внутренней поверхности труб, м. Зависимость коэффициента сопротивления λ от режима течения (Re) и  графически представлена на рис. 3.
графически представлена на рис. 3.

|
| Рис. 3. Зависимость коэффициента трения λ (для стальных труб) от критерия Re и степени шероховатости dэ / е. |
По уравнению (1.1) определяется плотность данного газа:
 .
.
Далее определяем скорость потока, зная массовый расход (уравнение 1.5):
 .
.
Коэффициент трения λ определяется из графической зависимости на рис. 3, предварительно рассчитывается критерий Re (формула 1.8) и dэ / е.
Таблица 1 – Плотность жидких веществ и водных растворов
| Вещество | Плотность, кг / м3 | |||||||||
| при –20 °С | при 0 °С | при 20 °С | при 40 °С | при 60 °С | при 80 °С | при 100 °С | при 120 °С | |||
| Азотная кислота | ||||||||||
| 100%-ная | ||||||||||
| 50%-ная | - | |||||||||
| Аммиак жидкий | ||||||||||
| Аммиачная вода 25%-ная | - | |||||||||
| Анилин | - | |||||||||
| Ацетон | ||||||||||
| Бензол | - | |||||||||
| Бутиловый спирт | ||||||||||
| Вода | - | |||||||||
| Гексан | ||||||||||
| Глицерин 50%-ный | - | |||||||||
| Двуокись серы (жидк.) | ||||||||||
| Дихлорэтан | ||||||||||
| Изопропиловый спирт | ||||||||||
| Кальций хлористый (25%-ный раствор) | ||||||||||
| Метиловый спирт | ||||||||||
| 100%-ный | - | |||||||||
| 40%-ный | - | |||||||||
| Муравьиная кислота | - | |||||||||
| Натр едкий, растворы | ||||||||||
| 50%-ный | - | |||||||||
| 40%-ный | - | |||||||||
| 30%-ный | - | |||||||||
| 20%-ный | - | |||||||||
| 10%-ный | - | |||||||||
| Натрий хлористый (20%-ный раствор) | - | |||||||||
| Нитробензол | - | |||||||||
| Октан | ||||||||||
| Олеум 20%-ный | - | |||||||||
| Серная кислота | ||||||||||
| 98%-ная | - | |||||||||
| 92%-ная | ||||||||||
| 75%-ная |
| |||||||||
| 60%-ная | ||||||||||
| Сероуглерод | ||||||||||
| Соляная кислота (30%-ная) | ||||||||||
| Толуол | ||||||||||
| Уксусная кислота | ||||||||||
| 100%-ная | - | |||||||||
| 50%-ная | - | |||||||||
| Фенол (расплавленный) | - | - | ||||||||
| Хлорбензол | ||||||||||
| Хлороформ | ||||||||||
| Четыреххлорис-тый углерод | ||||||||||
| Этилацетат | ||||||||||
| Этиловый спирт | ||||||||||
| 100%-ный | ||||||||||
| 80%-ный | - | |||||||||
| 60%-ный | - | |||||||||
| 40%-ный | - | |||||||||
| 20%-ный | - | |||||||||
| Этиловый эфир |
Таблица 2 – Вязкость жидких веществ и водных растворов
Коэффициент пересчета в систему СИ: спз . 10-3 = н . с / м2 = Па . с
| Вещество | Вязкость, спз | |||||||||||||
| при –20 °С | при –10 °С | при 0 °С | при 10 °С | при 20 °С | при 30 °С | при 40 °С | при 50 °С | при 60 °С | при 80 °С | при 100 °С | при 120 °С | |||
| Азотная кислота | ||||||||||||||
| 100%-ная | 1,49 | 1,24 | 1,05 | 0,92 | 0,8 | 0,72 | 0,64 | 0,57 | 0,5 | 0,39 | 0,35 | 0,31 | ||
| 50%-ная | - | 3,05 | 2,4 | 1,88 | 1,55 | 1,28 | 1,07 | 0,9 | 0,68 | 0,53 | 0,44 | |||
| Аммиак жидкий | 0,258 | 0,251 | 0,244 | 0,235 | 0,226 | 0,217 | 0,208 | 0,199 | 0,19 | - | - | - | ||
| Аммиачная вода 25%-ная | - | - | - | 1,72 | 1,3 | 1,05 | 0,855 | 0,71 | 0,6 | 0,42 | 0,32 | 0,23 | ||
| Анилин | - | - | 10,2 | 6,5 | 4,4 | 3,12 | 2,3 | 1,8 | 1,5 | 1,1 | 0,8 | 0,59 | ||
 Ацетон Ацетон
| 0,5 | 0,442 | 0,395 | 0,356 | 0,322 | 0,293 | 0,268 | 0,246 | 0,23 | 0,2 | 0,17 | 0,15 | ||
| Бензол | - | - | 0,91 | 0,76 | 0,65 | 0,56 | 0,492 | 0,436 | 0,39 | 0,316 | 0,261 | 0,219 | ||
| Бутиловый спирт | 10,3 | 7,4 | 5,19 | 3,87 | 2,95 | 2,28 | 1,78 | 1,41 | 1,14 | 0,76 | 0,54 | 0,38 | ||
| Вода | - | - | 1,79 | 1,31 | 1,0 | 0,801 | 0,656 | 0,549 | 0,469 | 0,357 | 0,284 | 0,232 | ||
| Гексан | 0,479 | 0,426 | 0,397 | 0,355 | 0,32 | 0,29 | 0,264 | 0,241 | 0,221 | 0,19 | 0,158 | 0,132 | ||
| Глицерин 50%-ный | - | - | 8,5 | 6,05 | 4,25 | 3,5 | 2,6 | 1,2 | 0,73 | 0,45 | ||||
| Двуокись серы (жидк.) | 0,455 | 0,41 | 0,368 | 0,334 | 0,304 | 0,279 | - | - | - | - | - | - | ||
| Дихлорэтан | 1,54 | 1,24 | 1,08 | 0,95 | 0,84 | 0,74 | 0,65 | 0,565 | 0,51 | 0,42 | 0,36 | 0,31 | ||
| Изопропиловый спирт | 10,1 | 6,8 | 4,6 | 3,26 | 2,39 | 1,76 | 1,33 | 1,03 | 0,8 | 0,52 | 0,38 | 0,29 | ||
| Кальций хлористый (25%-ный раствор) | 10,6 | 4,47 | 3,36 | 2,74 | 2,25 | 1,85 | 1,55 | - | - | - | - | |||
| Метиловый спирт | ||||||||||||||
| 100%-ный | 1,16 | 0,97 | 0,817 | 0,68 | 0,584 | 0,51 | 0,45 | 0,396 | 0,351 |
| 0,24 | 0,21 | ||
| 40%-ный | - | - | 3,65 | 2,54 | 1,84 | 1,37 | - | - | - | - | - | - | ||
| Муравьиная кислота | - | - | - | 2,25 | 1,78 | 1,46 | 1,22 | 1,03 | 0,89 | 0,68 | 0,54 | 0,4 | ||
| Натр едкий, растворы | ||||||||||||||
| 50%-ный | - | - | - | - | - | 8,03 | 5,54 | 3,97 | 3,42 | |||||
| 40%-ный | - | - | - | - | 9,2 | 5,44 | 3,62 | 2,72 | 2,37 | |||||
| 30%-ный | - | - | - | - | 6,3 | 4,6 | 3,4 | 2,16 | 1,82 | 1,71 | ||||
| 20%-ный | - | - | - | - | 4,48 | 3,3 | 2,48 | 1,63 | 1,27 | 1,15 | 1,08 | |||
| 10%-ный | - | - | - | - | 1,86 | 1,45 | 1,16 | 0,98 | 0,91 | 0,7 | 0,65 | 0,6 | ||
 Натрий хлористый (20%-ный раствор) Натрий хлористый (20%-ный раствор)
| - | 4,08 | 2,67 | 1,99 | 1,56 | 1,24 | 1,03 | 0,87 | 0,74 | 0,57 | 0,46 | 0,38 | ||
| Нитробензол | - | - | 3,09 | 2,46 | 2,01 | 1,69 | 1,44 | 1,24 | 1,09 | 0,87 | 0,7 | 0,58 | ||
| Октан | 0,968 | 0,829 | 0,703 | 0,61 | 0,54 | 0,479 | 0,428 | 0,386 | 0,35 | 0,291 | 0,245 | 0,208 | ||
| Олеум 20%-ный | - | - | 36,6 | 28,8 | 20,8 | 12,8 | 5,3 | - | - | |||||
| Серная кислота | ||||||||||||||
| 98%-ная | - | - | 25,8 | 17,1 | 12,9 | 9,46 | 7,5 | 4,1 | 2,7 | |||||
| 92%-ная | 23,1 | 15,6 | 11,8 | 8,4 | 6,7 | 3,8 | 2,5 | 1,95 | ||||||
| 75%-ная | 13,9 | 10,6 | 8,1 | 5,9 | 4,6 | 2,8 | 1,9 | 1,45 | ||||||
| 60%-ная | 10,5 | 7,7 | 5,52 | 4,08 | 3,42 | 2,8 | 2,4 | 1,5 | 1,07 | 0,9 | ||||
| Сероуглерод | 0,556 | 0,488 | 0,433 | 0,396 | 0,366 | 0,319 | 0,29 | 0,27 | 0,25 | 0,21 | 0,19 | 0,17 | ||
| Соляная кислота (30%-ная) | - | - | - | 2,1 | 1,7 | 1,48 | 1,3 | - | - | - | - | - | ||
| Толуол | 1,06 | 0,9 | 0,768 | 0,667 | 0,586 | 0,522 | 0,466 | 0,42 | 0,381 | 0,319 | 0,271 | 0,231 | ||
| Уксусная кислота | ||||||||||||||
| 100%-ная | - | - | - | - | 1,22 | 1,04 | 0,9 | 0,79 | 0,7 | 0,56 | 0,46 | 0,37 | ||
| 50%-ная | - | - | 4,35 | 3,03 | 2,21 | 1,7 | 1,35 | 1,11 | 0,92 |
| 0,5 | 0,4 | ||
| Фенол (расплавленный) | - | - | - | - | 11,6 | 4,77 | 3,43 | 2,56 | 1,59 | 1,05 | 0,78 | |||
| Хлорбензол | 1,48 | 1,24 | 1,06 | 0,91 | 0,8 | 0,71 | 0,64 | 0,57 | 0,52 | 0,435 | 0,37 | 0,32 | ||
| Хлороформ | 0,9 | 0,79 | 0,7 | 0,63 | 0,57 | 0,51 | 0,466 | 0,426 | 0,39 | 0,33 | 0,29 | 0,26 | ||
| Четыреххлорис-тый углерод | 1,9 | 1,68 | 1,35 | 1,13 | 0,97 | 0,84 | 0,74 | 0,65 | 0,59 | 0,472 | 0,387 | 0,323 | ||
| Этилацетат | 0,79 | 0,67 | 0,578 | 0,507 | 0,449 | 0,4 | 0,36 | 0,326 | 0,297 | 0,248 | 0,21 | 0,178 | ||
| Этиловый спирт | ||||||||||||||
| 100%-ный | 2,38 | 2,23 | 1,78 | 1,46 | 1,19 | 1,0 | 0,825 | 0,701 | 0,591 | 0,435 | 0,326 | 0,248 | ||
 80%-ный 80%-ный
| - | - | 3,69 | 2,71 | 2,01 | 1,53 | 1,2 | 0,97 | 0,79 | 0,57 | 0,52 | 0,43 | ||
| 60%-ный | - | - | 5,75 | 3,77 | 2,67 | 1,93 | 1,45 | 1,13 | 0,9 | 0,6 | 0,45 | 0,34 | ||
| 40%-ный | - | - | 7,14 | 4,39 | 2,91 | 2,02 | 1,48 | 1,13 | 0,89 | 0,6 | 0,44 | 0,34 | ||
| 20%-ный | - | - | 5,32 | 3,17 | 2,18 | 1,55 | 1,16 | 0,91 | 0,74 | 0,51 | 0,38 | 0,3 | ||
| Этиловый эфир | 0,364 | 0,328 | 0,296 | 0,268 | 0,243 | 0,22 | 0,199 | 0,182 | 0,166 | 0,14 | 0,118 | 0,1 |
Пример 1.1.5. Жидкость в количестве G, т/ч при температуре t перекачивается из реактора в напорный бак. В реакторе над жидкостью поддерживается разрежение Рвак, в напорном баке – атмосферное давление. Трубопровод диаметром d и длиной l. Жидкость перекачивается на высоту h. Сумма коэффициентов местных сопротивлений, имеющихся на трубопроводе Σζ. Коэффициент трения λ. Найти мощность, потребляемую насосом, приняв общий КПД насосной установки η.
РЕШЕНИЕ
Мощность, потребляемая двигателем насоса, может быть рассчитана по формуле:
 , ,
| (1.13) |
где N – мощность, кВт;
V – объемный расход, м3/с;
H – напор, создаваемый насосом, м;
ΔP – полное гидравлическое сопротивление сети, Па;
η – КПД насосной установки.
При этом студенту следует знать, что полное гидравлическое сопротивление сети определяется суммой следующих слагаемых
| ΔР = ΔРск + ΔРтр + ΔРм.с + ΔРпод + ΔРдоп, | (1.14) |
где  – затрата давления на создание скорости потока;
– затрата давления на создание скорости потока;
ΔРтр – потеря давления на трение (см. уравнение 1.10);
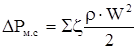 – потеря давления на преодоление местных сопротивлений;
– потеря давления на преодоление местных сопротивлений;
ζ – коэффициент местного сопротивления, который может быть найден из таблицы 3 "Коэффициенты местных сопротивлений";
ΔРпод = ρ . g . h – затрата давления на подъем жидкости;
ΔРдоп = Р2 – Р1 – разность давлений в пространстве нагнетания и в пространстве всасывания.
Зная массовый расход G, из уравнения (1.5) определяем скорость потока, потери давления на трение рассчитываем, как показано в примере 1.1.4.
В нашем примере ΔРдоп = Р2 – Р1 = Ратм – (Ратм – Рвак) = Рвак.
Определив полное гидравлическое сопротивление сети по уравнению (1.14), определяем мощность, потребляемую двигателем насоса (уравнение 1.13).
Таблица 3 – Коэффициенты местных сопротивлений
| Вид сопротивления | Значение коэффициента местного сопротивления ζ | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Вход в трубу

| С острыми краями: ζ = 0,5 С закругленными краями: ζ = 0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Выход из трубы

| ζ = 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Диафрагма (отверстие) с острыми краями в прямой трубе
 dотв – диаметр отверстия, м;
δ – толщина диафрагмы, м;
wотв – средняя скорость потока в отверстии, м/сек;
wт – средняя скорость потока в трубе, м/сек;
dотв – диаметр отверстия, м;
δ – толщина диафрагмы, м;
wотв – средняя скорость потока в отверстии, м/сек;
wт – средняя скорость потока в трубе, м/сек;
 ;
D – диаметр трубы, м ;
D – диаметр трубы, м
| Для  и и  потеря напора потеря напора  .
Значение ζ определяется по таблице .
Значение ζ определяется по таблице
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| m | 0,02 | 0,04 | 0,06 | 0,08 | 0,1 | 0,12 | 0,14 | 0,16 | 0,18 | 0,20 | 0,22 | ||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 86,0 | 65,5 | 51,5 | 40,0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| m | 0,24 | 0,26 | 0,28 | 0,30 | 0,34 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 32,0 | 26,8 | 22,3 | 18,2 | 13,1 | 8,25 | 4,00 | 2,00 | 0,97 | 0,42 | 0,13 | ||||||||||||||||||||||||||||||||||||||||||||||||
Колено или отвод круглого (квадратного) сечения плавный
 D – внутренний диаметр трубопровода, м;
Ro – радиус загиба трубы, м
D – внутренний диаметр трубопровода, м;
Ro – радиус загиба трубы, м
|
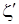 + ζтр + ζтр
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угол φ, градусы | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| А | 0,31 | 0,45 | 0,6 | 0,78 | 1,0 | 1,13 | 1,20 | 1,28 | 1,40 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Ro / d | 1,0 | 2,0 | 4,0 | 6,0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| В | 0,21 | 0,15 | 0,11 | 0,09 | 0,06 | 0,04 | 0,03 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
ζтр определяется так же, как для прямой трубы
[см. формулу (1.10)] длиной 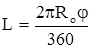
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Угольник (колено) 90о стандартный чугунный на резьбе | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Условный проход, мм | 12,5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 2,2 | 1,6 | 1,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вентиль нормальный | Значение ζ при полном открытии вентиля определяется по таблице: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D, мм | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 10,8 | 8,0 | 4,9 | 4,0 | 4,1 | 4,4 | 4,7 | 5,1 | 5,5 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Вентиль прямоточный | При  значение ζ определяется по таблице: значение ζ определяется по таблице:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| D, мм | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 1,04 | 0,85 | 0,79 | 0,65 | 0,60 | 0,50 | 0,47 | 0,36 | 0,32 | ||||||||||||||||||||||||||||||||||||||||||||||||||
При Re < 3 . 105 коэффициент сопротивления ζ = ζ1 . К
Значение ζ1 определяется так же, как и при Re 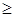 3 . 105, а величина К приведена ниже: 3 . 105, а величина К приведена ниже:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Re | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| К | 1,40 | 1,07 | 0,94 | 0,88 | 0,91 | 0,93 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Кран пробочный | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Условный проход, мм | 50 и выше | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задвижка | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Условный проход, мм | 15-100 | 175-200 | 300 и выше | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ζ | 0,5 | 0,25 | 0,15 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Внезапное
расширение
 Fo – площадь меньшего поперечного сечения, м2;
wo – скорость потока в меньшем поперечном сечении, м/сек;
F1 – площадь большего поперечного сечения, м2;
Fo – площадь меньшего поперечного сечения, м2;
wo – скорость потока в меньшем поперечном сечении, м/сек;
F1 – площадь большего поперечного сечения, м2;
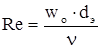 ; ;
 . .
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

| Fo / F1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3,1 | 3,1 | 3,1 | 3,1 | 3,1 | 3,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,7 | 1,4 | 1,2 | 1,1 | 0,9 | 0,8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2,0 | 1,6 | 1,3 | 1,05 | 0,9 | 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,0 | 0,7 | 0,6 | 0,4 | 0,3 | 0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| и более | 0,81 | 0,64 | 0,50 | 0,36 | 0,25 | 0,16 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
Внезапное сужение
 Fo – площадь меньшего поперечного сечения, м2;
wo – скорость потока в меньшем поперечном сечении, м/сек;
F1 – площадь большего поперечного сечения, м2;
Fo – площадь меньшего поперечного сечения, м2;
wo – скорость потока в меньшем поперечном сечении, м/сек;
F1 – площадь большего поперечного сечения, м2;
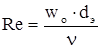 ; ;
 . .
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
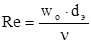
| Fo / F1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | |
| 5,0 | 5,0 | 5,0 | 5,0 | 5,0 | 5,0 | |
| 1,3 | 1,2 | 1,1 | 1,0 | 0,9 | 0,8 | |
| 0,64 | 0,50 | 0,44 | 0,35 | 0,30 | 0,24 | |
| 0,50 | 0,40 | 0,35 | 0,30 | 0,25 | 0,20 | |
| > 10000 | 0,45 | 0,40 | 0,75 | 0,30 | 0,25 | 0,20 |
1.1.1. Манометр на трубопроводе, заполненном жидкостью, показывает давление 0,18 кгс/см2. На какую высоту h над точкой присоединения манометра поднимается в открытом пьезометре вода, находящаяся в трубопроводе?
1.1.2. По трубам теплообменника, состоящего из 379 труб диаметром 16х1,5мм, проходит азот в количестве 6000 м3/ч (считая при 0 °С и 760 мм рт.ст.) под давлением Ризб = 2,5 кгс/см2. Азот входит в теплообменник при 110°С, выходит при 25 °С. Определить скорость азота в трубах теплообменника на входе и на выходе.
1.1.3. Определить режим течения этилового спирта в прямой трубе диаметром 40х2,5 мм. Скорость спирта 0,13 м/с, средняя температура 50 °С.
1.1.4. Определить потери давления на трение при протекании воды по латунной трубе диаметром 19х2 мм, длиной 10 м. Скорость воды 2 м/с, температура 55 °С. Принять шероховатость трубы е = 0,005 мм.
1.1.5. По водопроводной трубе проходит 10 м3/ч воды. Сколько воды в 1 ч пропустит труба удвоенного диаметра при той же потери напора на трение? Коэффициент трения считать постоянным.
1.1.6. По стальному трубопроводу внутренним диаметром 75 мм требуется перекачивать 25 м3/ч жидкости плотности 1200 кг/м3, с динамическим коэффициентом вязкости 1,7 мПа . с. Конечная точка трубопровода выше начальной на 24 м. Длина трубопровода 112 м, на нем установлены 2 прямоточных вентиля и 5 прямоугольных отводов с радиусом изгиба 300 мм. Трубы имеют незначительную коррозию. Найти потребляемую мощность, если общий КПД насосной установки 0,6.
1.1.7. По прямому воздухопроводу прямоугольного сечения 400х600 мм, сделанному из кровельной стали, надо подавать 14400 кг/ч воздуха при 30 °С и атмосферном давлении. Длина воздухопровода 60 м. Найти требуемую мощность электродвигателя, если его КПД – 0,95, а КПД вентилятора – 0,4.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
При изучении процессов осаждения следует обратить внимание на общность законов разделения как газовых, так и жидких неоднородных систем.
В настоящее время разработано много эффективных методов разделения таких систем, с которыми следует ознакомиться.
Это прежде всего процессы осаждения и отстаивания под действием силы тяжести и центробежной силы, фильтрование, мокрые способы осаждения пыли из газовых неоднородных систем. Нужно уяснить, что осаждение за счет центробежной силы является более эффективным по сравнению с осаждением под действием силы тяжести, так как скорость осаждения при действии центробежной силы увеличивается в несколько раз. Необходимо уяснить, что производительность отстойных аппаратов зависит только от площади осаждения и скорости осаждения и не зависит от их высоты. Следует обратить особое внимание на устройство наиболее эффективных разделительных аппаратов: непрерывно-действующих автоматических центрифуг, сверхцентрифуг, циклонных аппаратов, электрофильтров.
Приведенные ниже примеры и таблицы расчетных зависимостей помогут глубже изучить процессы осаждения (отстаивания).
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 725; Нарушение авторских прав?; Мы поможем в написании вашей работы!