Расчет разветвленной электрической цепи с одним источником энергии

Смешанное соединение (рис. 2.7)

Параллельное соединение (рис. 2.6)

Преобразования в электрических цепях

Законы Кирхгофа

Согласно первого закона Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю

∑ I = 0.

Поскольку речь идет об алгебраической сумме ∑ I, необходимо учитывать знаки слагаемых токов. Входящие в узел токи принято считать положительными, выходящие – отрицательными. Для узла "а" (рис. 2.5) имеем

I ₁ + I ₂ - I ₃ = 0.

Согласно второго закона Кирхгофа алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах контура

∑ E = ∑ R · I.

Для составления уравнения по второму закону Кирхгофа произвольно выбирают направление обхода контура. Принято ЭДС, токи и напряжения считать положительными, если они совпадают по направлению с направлением обхода контура, а если не совпадают – отрицательными. При обходе контура E ₁, E ₂, R ₂, R ₁ электрической цепи (рис. 2.5) по часовой стрелке имеем

E ₁ - E ₂ = R ₁· I ₁ - R ₂ I ₂.

При расчётах сложных электрических цепей применяют формулы последовательного (смотреть пункт 2.1), параллельного, смешанного соединения элементов, а также преобразования "треугольника" в "звезду" и обратно. Рассмотрим эти соотношения.

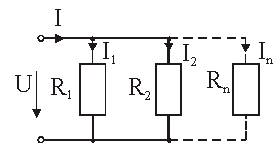
Рис. 2.6. – Параллельное соединение элементов

При таком соединении элементов общее сопротивление определяется выражением

При двух сопротивлениях, соединенных параллельно

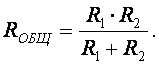
Если R ₁ = R ₂ = … R _n, то

где п – число параллельно соединенных элементов.

Смешанным соединением называют сочетание последовательного и парал­лельного соединений резисторов.

При смешанном соединении элементов для эквивалентного преобразования пользуются методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.

Поясним это на конкретном примере расчета электрической цепи (рис.1.3).

Рис.1.3. Смешанное соединение элементов.

Рис. 2.7. – Смешанное соединение элементов

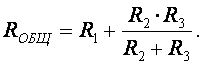
2.3.3. Преобразование "треугольника" в "звезду" (рис. 2.8)

2.2.4. Преобразование "звезды" в "треугольник" (рис. 2.8)

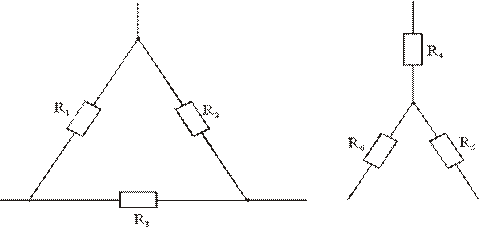
Рис. 2.8. – Соединение сопротивлений в "треугольник" и "звезду"

При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС, сопротивления элементов электрической цепи. Задача расчета электрической цепи сводится к определению токов в ветвях. По найденным токам можно рассчитать напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников, сечения проводников.

Для расчета электрических цепей с одним источником энергии применяется метод эквивалентных преобразований, заключающийся в постепенном преобразовании и замене последовательно и параллельно соединенных элементов эквивалентными. Всю группу элементов цепи заменяют одним эквивалентным. Преобразования начинают в ветвях, наиболее удалённых от источника. Затем в преобразованной (предельно простой) цепи по закону Ома определяют ток. Полученные в процессе преобразования расчетные схемы позволяют определить токи во всех остальных ветвях.

Пример 1: Рассчитать эквивалентное сопротивление цепи R_экв и, токи в каждом резисторе.

Дано: R ₁ = 3 Ом; R ₂ = 2 Ом; R ₃ = 5 Ом; R ₄ = 10 Ом; E = 50 В.

Рис. 2.9 - Пример эквивалентных преобразований:
а) схема электрической цепи до преобразования;
б) расчетная схема после первого преобразования;
в) - расчетная схема после второго (окончательного) преобразования

Определить токи в ветвях схемы, представленной на рис. 2.9, а.

Выбираем направления токов в ветвях. Преобразуем параллельно соединенные резисторы R ₂ и R ₃, заменяя их эквивалентным элементом R _{2, 3}

Расчетная схема после первого преобразования показана на рис. 2.9, б.

Проводим второе преобразование. Для этого последовательно соединенные резисторы R ₁, R _{2, 3}, R ₄ заменяем одним эквивалентным R _ЭКВ.

R _ЭКВ = R ₁ + R _{2, 3} + R ₄ = 3 + 1,43 + 10 = 14,43 Ом.

Теперь исходная схема сведена к простейшей, показанной на рис. 2.9, в, в которой

Для определения токов I ₂ и I ₃, необходимо определить напряжение U _аб, рис. 2.9, а, которое рассчитываем по рис. 2.9, б

U _аб = R _{2, 3}· I ₁ = 1,43·3,47 = 4,96 В.

Возвращаясь к схеме рис 2.9, а, получим

Для проверки правильности расчета токов составляем баланс мощности. Мощность, вырабатываемая всеми источниками энергии в цепи, должна быть равна мощности, потребляемой всеми приёмниками электрической энергии (нагрузкой). Относительная погрешность расчета не должна превышать одного процента.

Мощность, вырабатываемая источником ЭДС

Р _И = Е·I ₁ = 50·3,47 = 173,5 Вт.

Мощность, потребляемая нагрузкой

Погрешность баланса мощности

Если баланс сходится с допустимой погрешностью, то расчет токов выполнен верно.

Дата добавления: 2017-02-01