Даламбер принципі. 2 страница

Келтірілген масса (және инерция моменті) үшін,кинетикалық энергияның келтірілген массасының кинетикалық энергия массасымен теңестіру шартынан шыққан, оны ауыстыратын сөйлемді жазамыз:

Мұндағы және 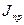келтірілген масса және келтірілген инерция моменті;

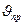және 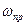келтіру буынының сызықтық және бұрыштық жылдамдығы;

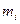және механизмнің i- ші буынының массасы және инерция моменті;

және механизмнің i- ші буынының сызықтық және бұрыштық жылдамдығы.

Осы теңдеулерден табатынымыз:

(1)

(2)

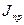Масса және инерция моментінің келтірілген мәндерінің арасында мынадай байланыс бар:

;

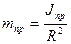Мұндағы 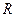орындаушы механизм органының оның айналу осіне қатысты радиусы (мысалы, қозғалу механизмдері үшін 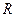- доңғалақ радиусы немесе жыланбауыр (гусеничный) жүрістің жұлдызшалары; стрелкалы кранның айналу механизмі үшін 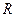- стрелка ұшынан (головка) кранның айналу осіне дейіңгі ара қашықтық; шығыр арқан (канатно-болочный) көтеру механизмі үшін 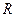- жүкарба (лебедка) атанағының (барабан) радиусы).

(1)теңдеуге сәйкес, жетекші доңғалақтарға келтірілген жиынтық айналушы және машинаның үдемелі қозғалыс жасайтын бөліктерінің массасы мынаған тең:

,

Мұндағы және доңғалақтың және қозғалтқыштың айналатын бөліктерінің инерция моменті;

және доңғалақтың және қозғалтқыш білігінің бұрыштық жылдамдықтары.

Қозғалтқыш білігінің бұрыштық жылдамдығының жетекші доңғалақтардың бұрыштық жылдамдықтарына көз қарасында, тартқыш жетегінің беріліс саны бар, алатынымыз:

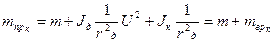,(3)

Сәйкесінше келтірілген жиынтық инерция моменті:

,(4)

(3) және (4) теңдеулердің соңғы екі мүшесімен, тартқыштың жетекші доңғалақтарына келтірілген масса және трансмиссияның айналатын бөліктеріне келтірілген инерция моментін анықтап алдық, яғни:

, .

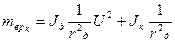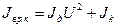2.Дәл осы массаны кез келген басқа орынға, мысалы, қозғалтқыш білігіне келтіруге болады. Бұл жағдайда және (2) формуладағыдай келтірілген жиынтық 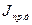инерция моменті, мынаған тең болады:

.

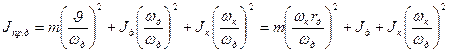Сәйкесінше қозғалтқыш білігіне келтірілген тартқыштың жиынтық массасы:

немесе .

(5) және (6) теңдеулердің соңғы екі мүшесінен, жетектің айналатын бөліктерінің келтірілген массасын және инерция моментін анықтаймыз, яғни:

; .

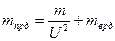№1 мысал. Орнынан қозғалған кездегі пневмодоңғалақты машинаның трансмиссия элементтеріне әсер ететін динамикалық салмақты анықтау(1 суерт).

Бастапқы берілгендер:

Машина массасы кг; доңғалақ радиусы 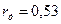м; қозғалтқыштың айналатын массасының және олармен тікелей байланысқан бөлшектердің инерция моменті 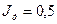кгм²; жетекші доңғалақтардың инерция моменті кгм²; трансмиссия ПӘК-і ; трансмиссияның беріліс саны ; машинаның орынан қозғалған кездегі жылдамдығы м/с; машина қозғалысына қарсылық 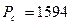Н.

Шешілуі:

1.Ұмтылыс кезіндегі машинаның қозғалатын бөліктеріне келтірілген (қозғалтқыш білігіне) жиынтық инерция моментін анықтаймыз:

.

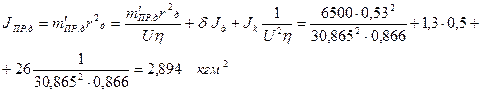2.Қозғалтқыш білігіндегі артық моментті анықтаймыз:

Нм.

3.Қозғалтқыш білігіндегі максимал динамикалық күшті анықтаймыз:

4.Жетекші доңғалақтардың жарты осіне салмақ салатын, максимал динамикалық моментті анықтаймыз:

Нм.

Практикалық жұмыс №5

Жүйе қозғалысының теңдеуін шешуге және құруға Лагранж әдісін және Даламбер принципін қолдану

Даламбер принципі бойынша жүйенің қозғалысында болатын уақыттың кез келген моментінің инерция күшінің теңесу орны, белсенді ішкі күштер және байланыс реакция күштері болады.

Бұл жағдайда қажетті және жеткілікті теңесу шартының геометриялық шарты нөлге тең болады және бұл күштердің моментінің мәні еркін А нүктесіне салыстырмалы, яғни:

;

,

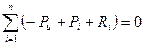Мұндағы 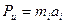- инерция күші; - белсенді күш; - жүйенің еркін массасына қойылатын, байланыс реакциясы; - 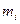массаның үдеуі.

2.Лагранж әдісі.

Лагранж теңдігі жалпыланған х координаты үшін мынадай түрі бар:

,

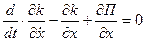Мұндағы 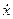- жалпыланған жылдамдық (уақыт бойынша туынды жалпылама координата);

- зерттеліп жатқан жүйенің кинетикалық энергиясы;

- оның потенциалдық энергиясы.

Жалпы түрде жүйенің кинематикалық энергиясы төмендегідей болады:

,

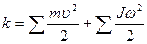Мұндағы .

Жүйенің потенциалдық энергиясы, жалпыланған күші жасайтын жұмыс түрінен анықталады.

3.Даламбер принципі бойынша жүйе қозғалысының теңдігін құру

Экскаватор шөмішінің тербелуін қарастырайық – көтеру атанағы тежелген кездегі, драглайнның арқаннан кенеттен түсірілуі (сурет 1).

Сурет 1. Драглайн қауғасының немесе шөмішінің арқаннан түсірілу кезіндегі тербелу есебінің сұлбасы

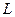жүктеме жоқ кездегі 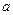және нүктелерінің арасындағы арқанның бос ұзындығы (см).

Онда арқандағы 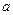– бөлігіндегі сызықтық қаттылық:

(1)

Мұндағы 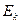- арқанның иілгіштік модулі, 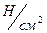; 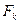- оның қиылысу ауданы, .

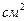1 суретте белгіленген:

- шөміштің ауырлық күші;

Мұндағы 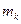- шөміштің және арқанның келтірілген массасы; 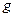- ауырлық күшінің үдеуі.

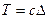- шөміш салмағынан арқанәсері,

Мұндағы - арқанның сызықтық қаттылығы; - бос шөміш кезіндегі арқанның деформациясы; - шөміштегі массалы топырақ салмағынан арқандағы қосымша деформация.

Шөмішті кенеттен түсіру моментін қарастырайық. Осы моментте шөмішке әсер етеді: - төменнен жоғарыға бағытталған, арқанның иілгіш күші

;

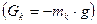- бос шөміштің ауырлық күші және - төменнен жоғарыға бағытталған, инерциялық күші. Қозғалыс теңдігі мынадай түрде болады:

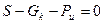немесе 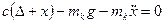(2)

Шөміш бос кезде, оған және 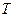күштері әсер етеді, бұл жағдайда қозғалыс теңдігі мынадай түрге ие болады:

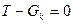немесе 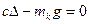(3)

Онда бос шөміштің қозғалысының шешуші соңғы теңдігі (2) және (3) формуладан анықталады:

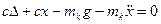
(4)

Бұл – шөміш тербелісінің өшпейтін дифференциал теңдеуі.

4.Жүйе қозғалысының теңдігін Лагранж әдісі бойынша құру.

Лагранж әдісін драглайн шөмішін кенеттен босату жағдайына қолданамыз, 1 суреттегі сұлбаға сәйкес келетіндей.

Кенеттен босатудан кейінгі, арқанның келтірілген массасын ескергендегі шөміштің кинематикалық энергиясы:

.

Потенциалдық энергия арқан ұзындығы қысқарған кезде шөмішті көтергеннен пайда болады, сондай-ақ шөмішті босату кезінде, көтергіш арқанның деформациясының потенциалдық энергиясы азайған кезде де пайда болады.

Тапсырманы шешу үшін, шөміш тербелісінің жоғарыда келтірілген мәндерін қабылдаймыз.

Шөмішті биіктікке көтерген кезде, босату әсерінен потенциалдық энергия көбейеді:

.

Екінші жағынан, иілгіш дене ретінде арқанның бастапқы потенциалдық энергиясы мынаны құрайды:

;

Соңғысы .

Бұл жағдайларда бұл шамалардың айырмашылығын арқанның потенциалдық энергиясының азаюмен анықталады:

.

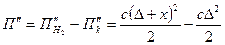Осылайша потенциалдық энергияның толық өсуі мынадай болады:

(5)

Лагранж теңдігінің барлық мүшелерін анықтаймыз:

;

;

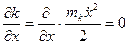(6)

(6) формуладан және басқа да көптеген практикалық тапсырмалардан шығатыны, жүйенің кинетикалық энергиясы жалпыланған жылдамдыққа тәуелді және жалпыланған координаталарын өзгерткен кезде де өзгеріссіз қалады:

.

Алынған формулаларды Лагранж теңдігіне қоя отырып, табатынымыз:

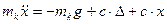немесе .

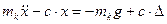Бірақ 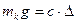болғандықтан, ізделіп отырған бос шөміш қозғалысының теңдігі мынадай болады:

(7)

Даламбер принципі бойынша алынған (7) және (4) теңдіктер ұқсас.

Лагранж әдісімен құрылған (7) теңдік, бұл жағдайда әрекеттегі күштерді және инерция күштерініңқозғалыс бағытын талап етпейді. Осы себептен де үдеудің және инерция күшінің бағыты белгісіз болған кезде Лагранж әдісі қиын жүйелер үшін жақсырақ,осы себептен де жоғары да келтірілген Даламбер әдісі қолданылмауы керек.

5.Драглайн шөмішінің бос тербелуі теңдігінің жалпы шешімі

Шөміштің бос тербелісінің дифференциал теңдігін (7) немесе (4) мынадай түрде көрсетуге болады:

, (8)

Мұндағы 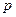- тербелудің циклдік жиілігі: . Берілген теңдіктің жалпы шешімі:

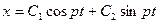(9)

(9) көрініп тұрғандай, шөміш қозғалысының тербелмелі қозғалысы бар, солайша және функциялары мерзімді болып келеді, 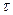интервал арқылы бір мәнді қабылдап отырады. Бұл уақыт интервалы тербелу периоды деп аталады:

.

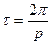Уақыт бірлігіндегі қозғалыстың қайтып-түсу санын тербелу жиілігі деп атайды:

.

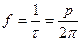Тұрақты 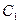және 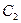интегралын анықтау үшін, бастапқы шарттарды қарау керек. Уақыттың бастапқы моментінде ; ; .

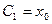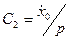Онда (9) теңдік болады:

.

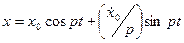Дата добавления: 2017-02-01