Ошибка интегрирования методом трапеций.

Метод трапеций.

Метод прямоугольников.

Пусть интервал (a,b) разбит на множество подынтегралов .

Будем считать, что на рассматриваемом подынтервале интегральная функция почти const . Тогда для данного подынтервала можно положить , где - произвольная точка на рассматриваемом подынтервале. Если в качестве такой точки взять среднюю точки подынтервала, получим , =>

где n – количество подынтервалов на отрезке интегрирования.

В методе трапеций принимается допущение, что функция на каждом подынтервале может быть приближена линейной функцией. При таком предположении интеграл заменяется площадью трапеции с высотой и основанием и . В результате получим формулу трапеции .

Пунктирной линией выделена трапеция, которой заменяется площадь под кривой интегрирования.

При интегрировании методом трапеций возникает ошибка, равная сумме площадей между кривой и хордами, соединяющими точки и .

Оценим ошибку, разлагая в ряд Тейлора в точке и . Это разложение позволит получить уравнение исходной кривой в виде, удобном для сравнения точного значения интеграла с приближенным. Рассмотрим разложение функции в ряд Тейлора в окружности точки . Предположим, что интегральная функция имеет столько производных, сколько нам необходимо.

Аналогично разложим для точки :

Обозначим длину подынтервалов через h, то есть и запишем формулу (7) в виде

.

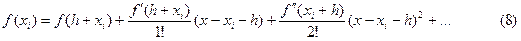Найдем среднее из формул (6) и (8):

Интегрируя 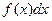в пределах получим .

Это выражение представляет собой оценку значений интеграла. Оценка может быть сделана как угодно точной, так как можно взять сколько угодно большое число членов разложения в ряд Тейлора.

В правиле трапеций, если в (9) отбросить все члены, содержащие h, получим ошибку метода трапеций .

Полную ошибку можно определить в следующем соотношении

.

Дата добавления: 2017-02-01