Сверхзвуковое сопло с косым срезом

Конические сопла Лаваля в нерасч-х усл-х.Реак-я сила

Сопло Лаваля – техническое приспособление, которое служит для ускорения газового потока проходящего по нему до скоростей, превышающих скорость звука. Широко используется на некоторых типах паровых турбин и является важной частью современных ракетных двигателей и сверхзвуковых реактивных авиационных двигателей.

Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами. Эффективные сопла современных ракетных двигателей профилируются на основании специальных газодинамических расчётов

Сопло Лаваля является основным элементом любого реактивного двигателя для создания реактивной тяги — силы, возникающей в результате взаимодействия двигательной установки с истекающей из сопла струёй газа, обладающего кинетической энергией. В основе возникновения реактивной тяги лежит закон сохранения импульса.

Реактивная тяга — сила, возникающая в результате взаимодействия двигательной установки с истекающей из сопла струёй расширяющейся жидкости или газа, обладающих кинетической энергией[1].

В основу возникновения реактивной тяги положен закон сохранения импульса. Реактивная тяга обычно рассматривается как сила реакции отделяющихся частиц. Точкой приложения её считают центр истечения — центр среза сопла двигателя, а направление — противоположное вектору скорости истечения продуктов сгорания (или рабочего тела, в случае не химического двигателя). То есть, реактивная тяга:

приложена непосредственно к корпусу реактивного двигателя;

обеспечивает передвижение реактивного двигателя и связанного с ним объекта в сторону, противоположную направлению реактивной струи

При расчетном режиме истечение из сверхзвукового сопла с косым срезом происходит с небольшими измене­ниями спектра потока. Эти изменения обусловлены влия­нием погранич-о слоя на стенке косого среза.

При нерасчетном режиме, когда давление среды р_а меньше расчетного (режим 1)> дополнительное расши­рение струи происходит в косом срезе или за его преде­лами. Если угол первой характеристики меньше, угла ко­сого среза ф, то расширение потока происходит за пре­делами косого среза. В этом случае кромки сопла А и Л! создают стационарные волны разрежения пересекающиеся не на оси струи, а в области, лежащей ближе к кром-ке А. По этой причине нарушается сим­метричность спектра истечения и струя отклоняется от оси сопла. Волны разрежения отражаются от границы струи, как волны сжатия (BCD_X и B\C_XD), пересекаю­щиеся вблизи противоположной границы. В зонах струи 2, примыкающих к границе, давление равно внеш­нему давлению р_а, в зоне 3 (за пересечением волн раз­режения) давление пониженное, а в зоне 4 — повыш-ое, = давлению в косом срезе сопла р\.

При перес-ии несимм-но распол-ой с-мы волн углы отк-ия линий тока мен-я от сеч-ия к сеч-ию. Соот-но меняется и средний угол отклонения струи.

Если первая волна разрежения из точки А частично или полностью лежит в пределах косого среза, то харак­тер течения меняется (рис. 6-34,6). Отраженная от стен­ки косого среза (частично или полностью) волна разре­жения приводит к понижению давления, и у кромки А давление оказывается меньшим, чем р_а. В рез-те в точке А обра-ся косой скачок уплотнения; с-ма волн изменяется и углы отклонения будут уже другими, по сравнению с первым случаем. В косом скачке AD ли­нии тока откл-ся по часовой стрелке, поэтому сред­ний угол откл-ия струи несколько увелич-ся. Та­кой хар-ер исте-ия будет иметь место в т. случае, когда угол косого среза <р <arc sin -щ.

Для второй группы режимов (давление среды выше расчетного) на кромках А и А\ возникают косые скачки (рис. 6-34,в), пересекающиеся за косым срезом, если угол Pi скачка из точки А_х меньше угла косого среза ф. Точка пересечения скачков В лежит у верхней границы струи. Поток отклоняется от оси струи, проходя несим­метричную систему скачков и отраженных волн разре­жения, причем поворот потока происходит в противопо­ложном первому случаю направлении. Заметим, что для первой группы режимов (р_а<р i), поворот струи проис­ходит относительно точки А, а при р_а>Р\ (вторая груп­па режимов) струя поворачивается относительно точ­ки А\. Углы откл-ия линий тока, а след-но, и всей струи меняются вдоль потока, так же как и в пер­вом случае, благодаря влиянию отраж-ых волн.

55. Основные характеристики и расчет диффузоров

При создании методики расчета сопла приняты следующие допущения:

· газ идеал-ый, его сост-ие опис-тся урав-ем Менделеева-Клапейрона;

· расход газа постоянен, течение установившееся;

· газ однороден и неизменен по составу;

· трение между газом и стенками сопла отсутствует;

· теплопередачи через стенки сопла не происходит;

· вязкость и трение между слоями газа пренебрежимо малы;

· скор-ь газа в попер-м сечении парал-на оси и один-ва во всех т-х сеч-я.

Уравнение движения. Рас-м одномерное неустанов-еся течение газа в цилиндр-й трубе перем-го сечения. Выделим V газа между двумя близкими сечениями, находящимися на расстоянии dx. Действие на этот объем стенок трубы и газа слева и справа заменим поверхностными силами, где Р — давление газа, Па; S — площадь поперечного сечения трубы, м².

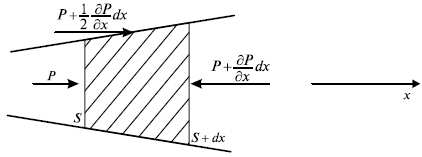Пусть выделенная частица газа объемом Sdx движется вправо под действием поверхностных сил. Второй закон Ньютона для нее записывается следующим образом:

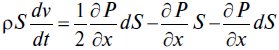
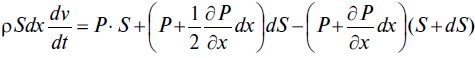где ρ — плотность, кг/м³; ν — скорость газа, м/с.

После несложных преобразований получим:

Уравнение неразрывности. Массовый расход газа G [кг/с] в любом сечении трубы постоянен и равен:

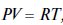Уравнение адиабаты. Уравнение состояния идеального газа (Менделеева-Клапейрона) для единицы массы газа записывается следующим образом:

Уравнение энергии. Рассмотрим течение газа в трубе переменного сечения без теплообмена со стенкой. Выбираем некоторый объем газа, ограниченный в начальный момент времени сечениями 1—2. За время dt частицы газа переместятся в новое положение, ограниченное сечениями1¹—2¹. Так как течение газа установившееся, то изменения энергии в общем для двух положений объеме между сечениями1¹—2 не будет, поэтому приращение энергии за время dt вычисляется как разность энергий в объемах1—2¹ и 1—1¹

Дата добавления: 2017-02-01