Рекуррентный алгоритм поиска решения МЦП

Автор: Вилисов Валерий Яковлевич, профессор кафедры Математики Технологического университета (г. Королев, Моск. обл.)

Рекуррентный алгоритм (РА) применяют для ограниченного числа шагов МЦП . Процедура выбора решений рассматривается как задача динамического программирования (ЗДП).

По аналогии с ЗДП оптимальный суммарный платеж 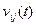, за оставшиеся t шагов, при перехода из -го состояния в j -ое (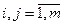), при условии принятия решения 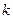, можно выразить через платеж за один шаг и оптимальный суммарный платеж за оставшиеся (t +1) шагов:

.

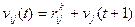А поскольку процесс может перейти из -го состояния в любое j -ое с вероятностью 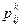, то условный (при условии выбора решения k) средний платеж:

.

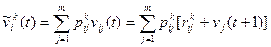Величина является целевой функцией (ЦФ) для выбора наилучшего k -го решения на t -ом шаге. Как и в ЗДП кроме решения ЦФ зависит и от текущего состояния i. Тогда, если платеж имеет смысл выигрыша, то уравнение Беллмана примет вид:

. (1)

А поскольку число шагов ограничено (N), то логично считать, что для (N +1)-го шага:

. (2)

Соотношение (1) представляет собой рекуррентное уравнение ЗДП, позволяющее найти оптимальное решение для каждого шага процесса. Поскольку в задаче (1)-(2) учитывается случайный характер выигрыша, её называют стохастической ЗДП.

Введя обозначение

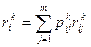, (3)

уравнение (1) для последнего шага, с учетом (2), можно записать в таком виде:

, (4)

а для остальных шагов:

, (5)

где 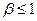- коэффициент дисконтирования.

Как и в ЗДП, условно-оптимальные решения отыскивается в обратном порядке (от последнего шага к начальному), а затем оптимальные – в прямом.

Алгоритм (4) - (5) можно применять и при нестационарных (изменяющихся по шагам) матрицах и .

Дата добавления: 2014-01-04