Наращенная величина аннуитета

Обобщающие характеристики финансовых потоков

Обобщающими характеристиками финансовых потоков являются:

• наращенная сумма;
• современная величина потока платежей.

Получатели поступлений оценивают свой доход суммарной величиной за полный срок действия платежа, разумеется, с учетом временной неравноценности денег.

Наращенная сумма – сумма всех платежей с начисленными на них процентами к концу срока ренты. Это может быть обобщенная сумма задолженности, итоговый объем инвестиций и т.п.

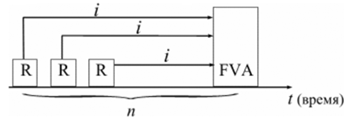
Рис. 7. Логика финансовой операции наращения финансовой ренты

Наращенные отдельные платежи представляют собой члены геометрической прогрессии с первым членом равным R и множителем равным (1 + i).

Рассмотрим определение наращенной суммы на примере наиболее простого случая, – годовой постоянной обычной ренты:

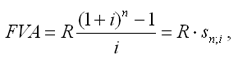
где FVA – наращенная сумма ренты;

R – размер члена ренты, т.е. размер очередного платежа;

i – годовая процентная ставка, по которой на платежи начисляются сложные проценты;

n – срок ренты в годах,

s _n;i – коэффициент наращения ренты.

Пример. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 руб., на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение:

Поскольку период ренты равен одному году, то это годовая рента; проценты начисляются один раз в год; взносы будут в конце периода ренты, постнумерандо, значит это обычная рента; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.

Сумма всех взносов с начисленными процентами будет равна:

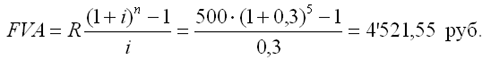
Можно определить наращенную сумму постоянной ренты, воспользовавшись финансовыми таблицами (Приложение 4), содержащими коэффициенты наращения ренты:

FVA = R • s _{5; 30} = 500 • 9,0431 = 4'521,55 руб.

Сумма взносов в течение 5 лет составит:

P = n • R = 5 • 500 = 2'500 руб.

Следовательно, сумма начисленных процентов будет равна:

I = FVA - P = 4'521,55 - 2'500 = 2'021,55 руб.

Таким образом, доход владельца счета за 5 лет составит 2'021,55 руб.

Для овладения методами финансовой математики важно не столько запоминание формул, сколько общих принципов расчета.

Для определения наращенной суммы на конец рассматриваемого периода последовательно присоединяются промежуточные результаты наращения к очередному платежу.

Рассмотрим поэтапное решение предыдущего примера:

Дата добавления: 2014-01-04