План погашения основной суммы долга равными частями

Погашение долга в рассрочку

План погашения долга единовременным платежом

Год	Долг (Dt)	Взносы в погасительный фонд, (Rt = Yt)	Накопленная величина в погасительном фонде, (St)	Проценты по долгу, (It)	Величина погашения текущего долга, (St-It)
	100'000	39'825,26	39'825,26	10'000	29'825,26
	110'000	39'825,26	84'031,30	11'000	84'020,30
	121'000	39'825,26	133'100,00	12'100	121'000,00
Итого	133'100	119'475,78	х	33'100	х

Как видно из таблицы, происходит ежегодное увеличение суммы долга за счет присоединения к нему процентов, поэтому к концу срока долг возрастет до 133'100 долларов, из которых выплата процентов составит 33'100 долларов. Однако за счет увеличения размера взносов в погасительный фонд общая величина обслуживания долга уменьшается.

В практике финансовой деятельности долг часто погашается в рассрочку, т.е. распределенными во времени платежами. При погашении основной суммы долга частями его текущее значение будет уменьшаться и, следовательно, сумма процентных платежей также будет уменьшаться.

Погашение долга частями также может осуществляться различными способами. В зависимости от преследуемых интересов стороны могут выбирать различные, удобные для них режимы в виде постоянных или переменных финансовых рент, а также нерегулярных потоков платежей.

7.1.2.1. Погашение основной суммы долга равными частями. Одним из вариантов погашения долга в рассрочку является погашение основной суммы долга равными частями.

При этом величина погашения долга определяется следующим образом:

d_t = D: n = const,

где d_t – величина погашения основной суммы долга;

D – первоначальная сумма долга;

n – срок долга в годах;

t – номер года, t = 1, 2, …, n.

Проценты начисляются на уменьшаемую сумму основного долга:

I_t = D_t • q,

где D_t – остаток долга на начало очередного года;

q – ставка процентов, начисляемых на сумму долга.

Тогда размер срочной уплаты можно представить как сумму процентов и сумму погашения долга:

Y_t = I_t + d_t,

где Y_t – срочная уплата на конец текущего года.

Пример. Сумма 100 тыс. долларов выдана под 10% годовых на 3 года. Определить величину срочной уплаты при погашении основной суммы долга равными ежегодными частями.

Решение:

Величина суммы погашения долга равна:

d_t = D: n = 100'000: 3 = 33'333,33 доллара.

Поскольку величина срочной уплаты при таком способе погашения долга меняется из года в год, то в этом случае без построения плана погашения долга в виде таблицы просто не обойтись.

Год (t)	Долг (D)	Сумма погашения долга (dt)	Выплата процентов (It)	Величина срочной уплаты (Yt)
	100'000,00	33'333,33	10'000,00	43'333,33
	66'666,67	33'333,33	6'666,67	40'000,00
	33'333,34	33'333,34	3'333,33	36'666,67
Итого	х	100'000,00	20'000,00	120'000,00

Таким образом, общие расходы по обслуживанию долга составили 120 тыс. долларов, из которых 20 тыс. долларов составляют проценты, а 100 тыс. долларов – погашение основной суммы долга. ^11>>>

7.1.2.2. Погашение долга и процентов по нему равными суммами в течение срока ссуды. Долг также можно погашать в рассрочку равными срочными уплатами, которые включают в себя как погашение основной суммы долга, так и величину процентов по нему:

Y_t = I_t + d_t = const.

При погашении долга в рассрочку величина долга систематически убывает, что приводит к уменьшению процентов и, соответственно, увеличению сумм, идущих на погашение долга, – это так называемое прогрессивное погашение.

Поскольку срочные уплаты равны, то их последовательность представляет собой финансовую ренту, современное значение которой должно быть равно сумме долга.

По формуле для определения размера платежа постоянной годовой финансовой ренты с выплатами в конце периода, размер срочной уплаты равен:

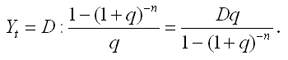
где Y_t – величина срочной уплаты;

D – первоначальная сумма долга;

q – процентная ставка на сумму долга;

n – срок долга в годах;

t – номер года, t = 1, 2, …, n.

Пример. Условия предыдущей задачи, но погашение долга предусматривает уплату равными срочными выплатами.

Решение:

Срочная уплата, включающая в себя погашение основной суммы долга и выплату процентов по долгу, равна:

Y_t = 100'000,00: 2,486851991 = 40'211,48 долларов.

Отсюда общие расходы по погашению долга равны:

Σ Y_t = 40'211,48 • 3 = 120'634,44 доллара.

Таким образом, ежегодные расходы по погашению долга будут составлять 40'211,48 долларов, а за весь срок финансовой операции – 120'634,44 доллара.

При этом варианте погашения долга также возможно построение таблицы.

Дата добавления: 2014-01-04