Характеристики

НОРМИРУЕМЫЕ МЕТРОЛОГИЧЕСКИЕ

ОЦЕНКА ПОЛНОЙ ПОГРЕШНОСТИ.

ЛЕКЦИЯ 21

Оценка полной погрешности. Если составлен алгоритм работы системы, то в ней можно выделить преобразования измерительной информации, сопровождающиеся погрешностями.

Очень важной задачей является определение полной погрешности ИИС по характеристикам погрешности этих функциональных преобразований или выполняющих их блоков.

В этой задаче можно выделить два предельных случая:

· определение полной погрешности одноканальной (последовательной) многоблочной ИИС;

· оценка погрешности ИИС многоканальной (параллельной) структуры.

Если известны аналитические выражения для законов распределения погрешностей отдельных звеньев и система линейна, то задача может быть решена с помощью методов свертки или с использованием характеристических функций.

Пусть, например, ε₁ и ε₂ — случайные функции погрешности двух соседних звеньев, a f(ε₁) и f(ε₂) —их плотности распределения. Тогда, если эти погрешности независимы, закон распределения суммарной погрешности ε_1,2 этих двух звеньев находится с помощью свертки исходных плотностей:

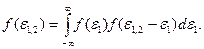
Применяя последовательно операцию свертки n—1 раз, где n— количество звеньев, получаем закон распределения полной погрешности системы.

Использование метода характеристических функций заключается в следующем. По теореме умножения характеристическая
функция суммы независимых случайных величин определяется как произведение их характеристических функций, т. е.:

где:

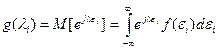
— характеристическая функция погрешности i-ro звена; g(λ_Σ) — характеристическая функция суммарной погрешности системы.

Выполнив затем обратное преобразование, можно найти закон распределения полной погрешности f(ε_Σ) системы.

Следует отметить, что инженерное решение задачи определения полной погрешности данными методами в большинстве случаев может быть получено лишь после преодоления трудностей, связанных с вычислением многомерных интегралов.

В настоящее время все большее значение приобретает развитие методов решения задачи определения полной погрешности, основанных на математическом моделировании. К ним относятся метод статистических испытаний (СИ) и метод деревьев логических возможностей (ДЛВ). Оба метода позволяют определить закон распределения полной погрешности как в случае, когда законы распределения погрешностей отдельных звеньев заданы аналитически, так и в случае, когда эти законы заданы в виде гистограмм.

Метод СИ является более разработанным и известным методом, чем метод ДЛВ. Сущность использования метода СИ для определения полной погрешности ИС заключается в следующем. Законы распределения случайных первичных погрешностей формируются с помощью специальных генераторов или программным путем. Осуществляя многократный перебор случайных сочетаний значений первичных погрешностей и определяя каждый раз полную погрешность, можно по результатам испытаний воспроизвести закон распределения полной погрешности ИС. Принципиально метод СИ не менее точен, чем аналитические методы расчета, но для получения высокой точности определения полной погрешности он требует перебора весьма большого количества случайных сочетаний первичных погрешностей.

Сущность метода ДЛВ заключается в следующем. Пусть имеется некоторое пространство логических возможностей. В этом пространстве может быть построено так называемое дерево, представляющее собой связный граф, в котором нет ни одного контура. Каждой ветви дерева приписывается некоторая вероятностная мера, представляющая собой безусловную или условную вероятность получения отдельных первичных погрешностей или возможного сочетания различных первичных погрешностей. Законы распределения погрешностей при использовании метода ДЛВ представляются в виде дискретной последовательности возможных значений первичных ошибок ε, каждому из которых приписывается определенная вероятность. Любое отдельное сочетание случайных значений различных первичных погрешностей представляет собой реализацию, вероятность которой определяется вероятностями выбранных значений первичных погрешностей. Каждая полученная описанным образом реализация образует вполне определенный путь в ДЛВ, и для нее сравнительно легко определить вероятность.

Метод ДЛВ может успешно использоваться для анализа погрешностей не только линейных, но и нелинейных систем, а также для случаев, когда случайные погрешности отдельных звеньев представляют собой не случайные величины, а случайные функции.

До сих пор речь шла о нахождении полной погрешности многозвенной измерительной системы по известным законам распределения. Как же следует поступать в тех случаях, когда частные погрешности заданы в виде некоторых числовых характеристик?

Если отдельные звенья ИС охарактеризованы экстремальными погрешностями, то полная погрешность системы определяется простым суммированием этих погрешностей. Естественно, такая оценка полной погрешности будет очень завышена.

Оценка полной погрешности может быть получена, если частные погрешности отдельных звеньев заданы интегральными оценками или доверительными интервалами и вероятностями.

Итак, полная систематическая погрешность многозвенной линейной ИС находится суммированием систематических погрешностей отдельных узлов (если, конечно, известны действительные систематические погрешности узлов, а не их доверительные интервалы, в последнем случае можно получить грубую верхнюю оценку), а дисперсия случайной погрешности при условии некоррелированности погрешностей отдельных звеньев — как сумма дисперсий погрешностей звеньев (в случае, если погрешности некоторых звеньев коррелированы между собой, к сумме дисперсий добавляются удвоенные корреляционные моменты соответствующих погрешностей). При суммировании вводятся весовые коэффициенты, зависящие от схемы включения звеньев и определяемые как частные производные от выходной величины системы по величине на входе данного звена. В том случае, если заданы не дисперсии случайных погрешностей отдельных звеньев, а их доверительные интервалы, для определения полной погрешности необходимо знание законов распределения частных погрешностей. По известным законам распределения частных погрешностей, доверительным интервалам и вероятностям можно найти дисперсии, а затем полученные дисперсии суммировать.

Если же законы распределения частных погрешностей неизвестны и заданы только их доверительные интервалы, то расчет полной погрешности становится крайне затруднительным. Из-за этого в качестве критерия погрешности отдельных звеньев предпочтительнее использовать среднее квадратическое отклонение или дисперсию.

В заключение следует сказать несколько слов о погрешности, с которой может определяться полная погрешность системы. В зависимости от решаемых задач эта погрешность должна выбираться разной. В обычных случаях эта погрешность может составлять примерно 30% максимального значения результирующей погрешности.

Оценка погрешности ИС многоканальной (параллельной) структуры может проводиться с учетом следующих соображений. Систематическая погрешность такой системы находится как среднее арифметическое систематических погрешностей Мε каждого из N каналов. Среднее значение случайной погрешности в каждом из N одинаковых каналов должно быть равно нулю, поэтому равно нулю и среднее значение случайной погрешности системы в целом. Дисперсия случайной погрешности системы равняется среднему значению дисперсий случайной погрешности Dε в каждом канале.

Если в системе не все каналы однородны, а имеется несколько различающихся между собой групп однородных каналов, то такие средние показатели могут формироваться для каждой группы в отдельности.

Нормируемые метрологические характеристики. Под метрологическим обеспечением автоматизированных систем измерения (АСИ) понимается комплекс мер, направленных на достижение и поддержание в этих системах требуемой точности измерения. Метрологическое обеспечение АСИ на стадиях их разработки, производства и эксплуатации решает различные задачи.

На стадии проектирования должны быть выполнены метрологическая экспертиза проектов технических заданий и документации на АСИ, разработка технических средств и методик метрологической аттестации и поверки АСИ, государственные или ведомственные приемочные испытания или метрологическая аттестация (для АСИ единичного производства), метрологический надзор за разработкой АСИ.

Метрологическое обеспечение АСИ на стадии производства включает главным образом контрольные испытания и метрологический надзор за технической документацией и технологией изготовления АСИ.

При внедрении АСИ, комплектуемых на объектах эксплуатации из агрегатированных средств, должна проводиться метрологическая аттестация измерительных каналов АСИ и методик выполнения измерении. Эти работы должны обязательно делаться и для АСИ, основанных на использовании выпускаемых промышленностью (ИВК).

В период эксплуатации должны быть обеспечены метрологическая аттестация АСИ в случае, если условия работы отличаются от тех, при которых нормировались их метрологические характеристики, аттестация после ремонта, периодические поверки, надзор и контроль за применением АСИ.

Кроме перечисленного в метрологическое обеспечение должны входить методики выполнения измерений (МВИ) и испытаний (МИ). Под методикой выполнения измерения понимают рекомендации по выбору технических средств и методов их применения, а также оценок результатов измерений. Проводится работа по законодательному закреплению этих методик.

ГОСТ 8.437-81 регламентирует работу метрологических служб Госстандарта, министерств и предприятий, а также определяет содержание основных работ по метрологическому обеспечению АСИ (далее информационно-измерительная система (ИИС)).

По метрологическому обеспечению средств измерений имеется ряд государственных стандартов [ГОСТ 8.437-81. Системы информационно-измерительные. Метрологическое обеспечение. Основные положения.; ГОСТ 22317-77. Средства агрегатные информационно-измерительных систем. Общие требования к комплексам нормируемых характеристик.; ГОСТ24130-80. Средства агрегатные информационно-измерительных систем аналого-цифровые. Основные нормируемые характеристики.; ГОСТ 8.009-72. Нормируемые метрологические характеристики средств измерений]. Остановимся далее на наиболее важной и ответственной части метрологического обеспечения ИИС, заключающейся в определении комплекса нормируемых метрологических характеристик (MX) и разработке методов и средств поверок MX основной разновидности ИИС — измерительных систем.

Комплекс нормируемых метрологических характеристик ИС должен позволить с должной достоверностью оценить погрешности результатов измерений, получаемых с помощью ИС, относительно просто выполнять операции поверки и обеспечить оценку метрологических свойств как большого количества, так и конкретных экземпляров ИС данного типа.

В любой ИС можно выделить измерительный канал, т. е. совокупность преобразователей информации, начиная от входа и кончая выходом системы, и измерительные компоненты, выполняющие часть преобразований канала системы. К измерительным компонентам ИС можно отнести, например, датчики, измерительные цепи, аналоговые и цифровые устройства, линии связи и т. п. MX измерительных компонентов ИС определяются так же, как и для средств измерения вообще. Нормированию в ИС подлежат MX измерительных каналов.

Методы регламентации и определения MX измерительных каналов ИС следует выбирать в зависимости от особенностей систем.

Нормирование MX измерительных каналов предпочтительнее регламентировать для таких выпускаемых заводом-изготовителем ИС, которые характеризуются постоянным составом несущественно разнесенных в пространстве компонентов, легким доступом для выполнения контроля, последовательной, параллельной или параллельно-последовательной (с небольшим количеством параллельных каналов) структурой. Метрологический контроль в этом случае осуществляется путем проверки соответствия MX измерительных каналов нормированным значениям.

Определение MX измерительных каналов системы расчетным или экспериментальным путем предпочтительнее осуществлять для ИС, комплектуемых при монтаже на месте эксплуатации, для ИС с существенной пространственной разнесенностью компонентов, с большим числом сменных компонентов, с затрудненным доступом к ИС в целях ее контроля.

Наконец, оценку MX измерительных каналов системы расчетным путем целесообразно устанавливать для ИС, отличающихся переменной структурой и связями между компонентами, а также большим количеством параллельных каналов. При этом контролируются MX измерительных компонентов, a MX каналов определяются расчетным путем.

Экспериментальные методы определения MX измерительных каналов ИС разумно применять для ИС, в которых влияние взаимодействия компонентов на MX трудно оценить заранее.

В технической документации на ИС определяются условия контроля MX: объем выборки, допустимая погрешность измерения, минимально допустимое количество точек и их расположение в диапазоне измерения, условия проведения экспериментов. Метрологические характеристики алгоритма вычислений контролируются экспериментальным или расчетным методом на правильность регламентированных значений.

Приведем соображения о нормировании MX измерительных каналов ИС в соответствии с ГОСТ 8.009-72.

Конкретный состав MX уточняется для каждой ИС на стадии разработки технического задания. При оценке нормируемых MX необходимо учитывать, что погрешности оценок MX являются величинами второго порядка малости по сравнению с результатами измерений. Это обстоятельство позволяет применять приближенные методы оценки MX ИС.

К нормируемым MX основной погрешности Δ относятся:

-моменты систематической составляющей M[Δ_S], D [Δs] или σ [Δ s], отражающие свойства всей совокупности ИС данного типа, для которого они нормированы, и предельное значение погрешности Δ sp;

-D [Δо] для некоррелированной случайной погрешности Δ о;

-R _Δ о(τ) для коррелированной погрешности Δo;

- предельное значение случайной погрешности от трения и гистерезиса Δонр (обычно D [Δон] =Нор²/12);

- функции влияния ψ(ξ) как зависимости изменения нормируемой MX от изменения влияющих величин в пределах условий применения; если функции линейны, т. е. ψ_ΔS(ξ) = AΔξ, A=соnst, то М [ψ_ΔS(ξ)] =АМ (Δξ), a D [ψ_ΔS(ξ)] = A²D (Δξ);

-передаточная функция, переходная, импульсная, амплитудно-фазовая и другие характеристики для оценки динамических свойств.

Могут нормироваться входные и выходные полные сопротивления ИС для электрических величин. При измерении же неэлектрических величин следует выявить характеристики взаимных влияний между объектом исследования и ИС, а затем решить вопрос о нормировании этих характеристик.

Помимо указанных могут регламентироваться характеристики, специфические для данной ИС, например для телеизмерительной системы — параметры линий связи, при которых гарантируются установленные MX системы.

Экспериментально определяются MX измерительных каналов конкретных экземпляров ИС: индивидуальная функция преобразования, поправки к показывающим и регистрирующим устройствам измерительного канала, характеристики следующих погрешностей: Δ_SH и Δ_SB — границы интервала неисключенной систематической составляющей и вероятности Р_ΔS или нижней границы Р_ΔSH ее допустимых значений, σ(Δ₀), R Δ₀(τ) или S Δ₀(ω) —среднего квадратического отклонения, нормированной корреляционной функции или спектральной плотности мощности случайной составляющей погрешности с указанием погрешности определения этих характеристик, вариация гистерезиса.

Экспериментально определяются индивидуальные динамические характеристики измерительного канала (передаточная функция, переходная характеристика и т. п., время реакции измерительного канала), чувствительность к влияющим воздействиям, взаимодействие между объектом исследования и измерительным каналом, а также между измерительными каналами.

Погрешности экспериментального определения MX рекомендуется выражать в виде границ интервала возможных значений погрешности и вероятности, с которой погрешность находится в этом интервале.

Дата добавления: 2014-01-04