Деревья

Var

Файлы без типа

Лекция 14

Применение плазменного напыления в стоматологии.

Нанесение ретенционного слоя микроплазменным методом в стоматологии начало свое развитие с 1992 года. В последние годы технологию плазменного напыления все шире используется в ортопедической стоматологии.

Метод плазменного напыления позволил поднять ортопедическую стоматологию на качественно новый уровень, то есть отказаться от коронки по Белкину, шариков-перлов, ретенционных элементов в виде пропилов, козырьков и т.д., часто не удовлетворяющих предъявляемыми требованиям. Толщина адгезионного слоя минимальна, что избавляет врача от препарирования большого объема ткане й зуба.

С помощью плазменного напыления появилась возможность наносить ретенционные покрытия на одиночные литые и штампованные коронки, паянные и цельнолитые мостовидные протезы, вкладки и бюгеля, а также отдельные части их поверхности.

После нанесения ретенционного слоя рекомендуется покрытие нитридом титана (TIN), который повышает коррозийную устойчивость протезов, улучшает эстетические свойства видимых частей протеза.

Для облицованного покрытия могут быть использованы различные марки пластмассы синма, изозит, суперпонт, солидекс и др. имеющиеся материалы. Пластмассовые покрытия наносятся по традиционной обще принятой технологии с использованием маскировочных покрытий типа «CANALOR».

В 2004 году фирмой ООО НПП «Форса ДЕНТ» начало производства нанесения плазменного покрытия (ретенция) на зубопротезную продукцию.

< Объявление файловой переменной для файла без типа >::=

F: File;

Процедуры и функции для работы с файлами без типа

procedure Assign(var F: File; FileName: string);

procedure Close (var F: File);

procedure Seek(var F: File, RecordNumber: Longint);

procedure Truncate(var F: File);

procedure Read(var F: File; < Список ввода >);

procedure Write(var F: File; < Список вывода >);

function Eof(var F: File): boolean;

Отличия:

procedure Reset(var F: File [, RecordSize: Longint]);

procedure Rewrite(var F: File [, RecordSize: Longint]);

Если параметр RecordSize указан, он задаёт длину записи (в байтах).

Если он не указан, считается, что RecordSize=128. Вот так.

Новые процедуры:

procedure BlockRead(var F: File; var Buffer; Count: Integer

[; var AmtTransferred: Integer]);

Параметр Buffer – имя любой переменной (например, имя большого массива), в которую будут читаться данные из файла.

Параметр Count – количество записей, которое следует прочесть из файла. Таким образом, будет предпринята попытка прочесть Count * RecordSize байт из файла. Если в переменную Buffer такое количество не вместится (т.е. будет испорчена память за переменной Buffer), ответственность за тяжкие последствия несёт программист.

Параметр AmtTransferred, если он присутствует, показывает, сколько в действительности записей удалось прочитать. AmtTransferred < Count в том случае, если…. Впрочем, сообразите сами.

procedure BlockWrite(var F: File; var Buffer; Count: Integer

[; var AmtTransferred: Integer]);

Параметр Buffer – имя любой переменной, из которой будут записываться данные в файл.

С прочими параметрами, хочется надеяться, всё ясно.

Определение. Дерево с базовым типом T – это:

1) либо пустое дерево,

2) либо некоторая вершина типа T с конечным числом связанных с ней отдельных деревьев с базовым типом T, называемых поддеревьями.

Из сходства рекурсивных определений последовательностей и деревьев ясно, что последовательность (список) есть дерево, в котором каждая вершина имеет не более одного поддерева. Поэтому последовательность (список) называют иногда и вырожденным деревом.

Способы изображения дерева:

a)

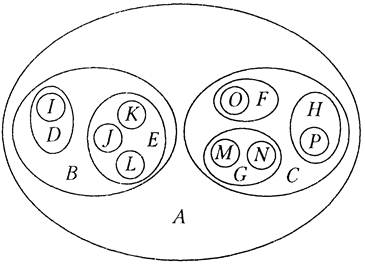
b) (A (B (D (I), E (J, K, L)), C (F (O), G (M, N), H (P)))

c) A B D I E J K L C F O G M N H P

d)

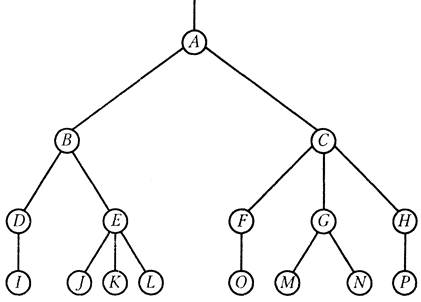
Упорядоченное дерево – это дерево, у которого ребра (ветви, дуги), исходящие из каждой вершины, упорядочены. Поэтому два упорядоченных дерева

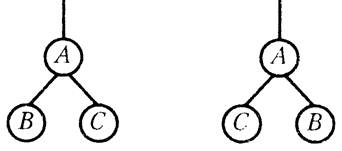
– это разные, отличные друг от друга объекты. Вершина Y, находящаяся непосредственно ниже вершины X, называется непосредственным потомкомX; если X находится на уровне 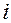, то говорят, что Y лежит на уровне 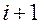. И наоборот, вершину X называют (непосредственным) предком вершины Y. Считается, что корень дерева находится на уровне 0. Максимальный уровень какой-либо из вершин дерева называется его глубиной или высотой.

Если элемент не имеет потомков, то его называют терминальной вершиной или листом, а нетерминальную вершину называют внутренней.

Число непосредственных потомков внутренней вершины называют ее степенью. Максимальная степень всех вершин есть степень дерева.

Число ветвей или ребер, которые нужно пройти от корня к вершине X, называется длиной пути к X. Корень имеет длину пути 0, его прямые потомки имеют путь длиной 1 и т. д. Вообще, вершина на уровне 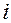имеет длину пути 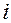. Длина пути всего дерева определяется как сумма длин путей для всех его компонент. Ее также называют длиной внутреннего пути. Например, длина внутреннего пути дерева

(A (B (D (I), E (J, K, L)), C (F (O), G (M, N), H (P)))

равна 36.

Средняя длина пути

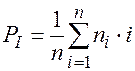
где 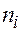— число вершин на уровне .

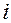Для того чтобы определить, что называется длиной внешнего пути, дополним дерево специальными вершинами в тех местах, где в исходном дереве отсутствуют поддеревья. Причем будем предполагать, что все вершины должны быть одной и той же степени, а именно степени дерева. Следовательно, такое расширение дерева порождает вместо пустых ребер массу специальных вершин, которые, конечно, уже не имеют потомков. На рис. 4.19 показано такое расширенное специальными вершинами дерево с рис. 4.17, специальные вершины отмечены квадратиками. Длина внешнего пути теперь может быть определена как сумма длин путей всех специальных вершин. Если число специальных вершин на уровне 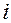равно 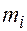, то средняя длина внешнего пути

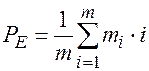
Длина внешнего пути дерева

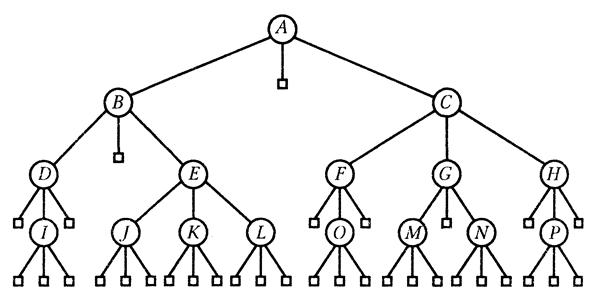
равна 120. Число специальных вершин 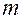, которые добавляются к дереву степени , прямо зависит от числа его исходных вершин 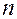. К каждой вершине ведет только одно ребро. Таким образом, в расширенном дереве всего 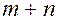ребер. С другой стороны, из каждой исходной вершины выходят ребер, а из специальных – ни одного. Поэтому всего имеется 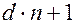ребро (1 дает ребро, идущее к корню). Из этих двух формул получается уравнение, связывающее число специальных вершин 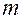с числом исходных вершин :

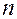или

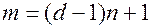
Максимальное число вершин в дереве высотой 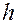достигается в том случае, если из каждой вершины, за исключением находя­щихся на уровне 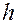, исходят поддеревьев. В этом случае для деревьев степени на уровне 0 находится одна вершина (корень), уровень 1 содержит потомков, на уровне 2 размещены 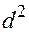по­томков вершин уровня 1 и т. д.

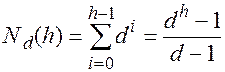
есть максимальное число вершин в дереве высотой h и степени . При :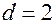

.

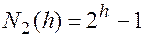Особенно важную роль играют упорядоченные деревья второй степени. Их называют двоичными (или бинарными) деревьями.

Определим упорядоченное двоичное дерево как конечное множество элементов (вершин), которое либо пусто, либо состо­ит из корня (вершины) с двумя отдельными двоичными деревь­ями, которые называются левым и правым поддеревом этого кор­ня. Везде далее в этом разделе мы будем иметь дело только с дво­ичными деревьями, поэтому если мы говорим дерево, то это означает упорядоченное двоичное дерево. Деревья степени боль­ше двух называются сильно ветвящимися деревьями (multiway trees), о них речь пойдет чуть позже.

Знакомые для нас примеры двоичного дерева: генеалогическое (семейное) дерево, где у каждого человека есть потомки (!!!) в лице отца и матери; схема теннисного (футбольного, снукерного и т.п.) турнира, где каждая игра – это вершина, обозначенная ее победителем, а предки – две предыду­щие игры соперников; арифметическое выражение с бинарными операциями, где каждому оператору соответствует вершина, а операнды – поддеревья.

Дата добавления: 2014-01-03