
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Матрицы. Операции над матрицами
|
|
|
|
КУРСК 2011
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
ПО МАТЕМАТИКЕ
КОНСПЕКТ ЛЕКЦИЙ
Дроздов В.И.
(РАБОЧАЯ ТЕТРАДЬ)
| 1. | Матрицы. Операции над матрицами…………………………..… | |||
| 1.1. | Пример 1.1………………………………………………….. | |||
| 1.2. | Пример 1.2………………………………………………….. | |||
| 1.3. | Пример 1.3………………………………………………….. | |||
| 2. | Определители…………………………………………………..…. | |||
| 2.1. | Пример 2.1……………………………………………….….. | |||
| 2.2. | Пример 2.2………………………………………….……….. | |||
| 2.3. | Пример 2.3………………………………………….……….. | |||
| 2.4. | Пример 2.4……………………………………………….….. | |||
| 3. | Ранг матрицы……………………………………………..……….. | |||
| 3.1. | Пример 3.1……………………………………………….….. | |||
| 3.2. | Пример 3.2……………………………………………….….. | |||
| 4. | Обратная матрица ………………………………………................ | |||
| 4.1. | Пример 4.1………………………………………….……….. | |||
| 4.2. | Пример 4.2………………………………………….……….. | |||
| 5. | Системы линейных уравнений. Критерий совместности Кронекера-Капелли…………………………………………….…. | |||
| 5.1. | Пример 5.1……………………………………………….….. | |||
| 6. | Матричный метод…………………………………………………. | |||
| 6.1. | Пример 6.1……………………………………………….….. | |||
| 7. | Формулы Крамера……………………………………..………..… | |||
| 7.1. | Пример 7.1………………………………………………..….. | |||
| 8. | Метод Гаусса……………………………………………………….. | |||
| 8.1. | Пример 8.1………………………………………………..….. | |||
| 8.2. | Пример 8.2……………………………………………….….. | |||
| 8.3. | Пример 8.3………………………………………….………... | |||
| 9. | Системы линейных уравнений общего вида…………………..… | |||
| 9.1. | Методы исследования…………………………………….… | |||
| 9.2. | Собственные числа и собственные векторы……………… | |||
| 9.3. | Пример 9.1…………………………………………………... | |||
| 9.4. | Пример 9.2…………………………………………………... | |||
| 9.5. | Пример 9.3…………………………………………………... | |||
| 9.6. | Пример 9.4…………………………………………………... | |||
| 10. | Использование систем линейных уравнений………………….... | |||
| 10.1 | Пример 10.1………………………………………………… | |||
| 10.2 | Пример 10.2………………………………………………… | |||
| 10.3 | Пример 10.3……………………………………………….… | |||
| 10.4 | Пример 10.4………………………………………………… | |||
| 10.5 | Пример 10.5………………………………………………… | |||
| 10.6 | Пример 10.6………………………………………………… | |||
| ЛИТЕРАТУРА…………………………………………………….. | ||||
| ПРИЛОЖЕНИЯ…………………………………………………… | ||||
СОДЕРЖАНИЕ
Прямоугольной матрицей размера m на n называется совокупность 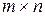 чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
чисел, расположенных в виде прямоугольной таблицы, содержащей m строк и n столбцов. Мы будем записывать матрицу в виде
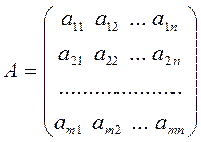 (1.1)
(1.1)
или сокращенно в виде 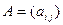 (i =
(i =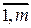 ; j =
; j = 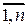 ). Числа
). Числа 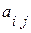 составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы
составляющие данную матрицу, называются ее элементами; первый индекс указывает на номер строки, второй - на номер столбца. Две матрицы 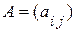 и
и 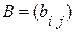 одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если
одинакового размера называются равными, если попарно равны их элементы, стоящие на одинаковых местах, то есть A = B, если 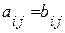 .
.
Матрица, состоящая из одной строки или одного столбца, называется соответственно матрицей-строкой или матрицей-столбцом.
Матрица, состоящая из одного числа, отождествляется с этим числом. Матрица размера 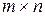 , все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n.
, все элементы которой равны нулю, называются нулевой матрицей и обозначается через 0. Элементы матрицы с одинаковыми индексами называют элементами главной диагонали. Если число строк матрицы равно числу столбцов, то есть m = n, то матрицу называют квадратной порядка n.
Квадратные матрицы, у которых отличны от нуля лишь элементы главной диагонали, называются диагональными матрицами и записываются так:
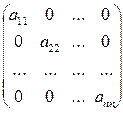
.
Если все элементы 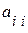 диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:
диагональной матрицы равны 1, то матрица называется единичной и обозначается буквой Е:

Квадратная матрица называется треугольной, если все элементы, стоящие выше (или ниже) главной диагонали, равны нулю. Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком Т наверху.
Пусть дана матрица (1.1). Переставим строки со столбцами. Получим матрицу
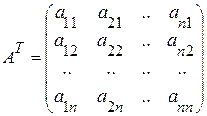
которая будет транспонированной по отношению к матрице А. В частности, при транспонировании матрицы-столбца получается матрица-строка и наоборот.
Для заметок
Произведением матрицы А на число λ называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число λ:
λ A = 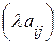 .
.
Суммой двух матриц A = 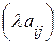 . И B =
. И B = 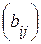 . одного размера называется матрица C =
. одного размера называется матрица C = 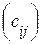 того же размера, элементы которой определяются по формуле
того же размера, элементы которой определяются по формуле
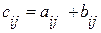
Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением двух матриц A = 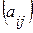 и B =
и B = 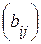 , где i =
, где i =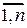 , j=
, j=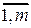 , k=
, k=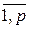 , заданных в определенном порядке АВ, называется матрица
, заданных в определенном порядке АВ, называется матрица 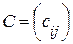 , элементы которой определяются по следующему правилу:
, элементы которой определяются по следующему правилу:
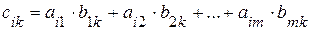 (1.2)
(1.2)
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 463; Нарушение авторских прав?; Мы поможем в написании вашей работы!