Моделирование и анализ САУ

Классификация САУ

Основным классификационным признаком САУ является используемый для ее построения принцип управления (см. раздел 2.1). При этом существует еще ряд признаков, которые используются для классификации систем управления.

2.2.1. По характеру изменения задающего воздействия (цели управления)

В зависимости от характера изменения задающего воздействия x (t) системы управления делятся на [1, 8-10, 16]:

1) обычные САУ, к которым относятся:

- САУ автоматической стабилизации;

- САУ программного регулирования;

2) следящие САУ.

В обычных САУ значение или закон изменения задающего воздействия x (t) заранее известны, заданы, а целью управления является обеспечение соответствующего значения или закона изменения управляемой величины y (t).

В системах автоматической стабилизации задающее воздействие представляет собой постоянную величину. Областью применения таких САУ являются непрерывные технологические процессы, в которых управляемый параметр нужно поддерживать в постоянном значении. В системах программного управления задающее воздействие является заранее известной функцией времени (изменяется по закону, заданному программой). Такие системы оснащаются программными задатчиками, формирующими задающее воздействие, изменяющееся во времени (см., например, САУ температурой электронагревательного элемента на рис. 7). Область применения: управление периодическими процессами.

Все примеры САУ, рассмотренные в разделе 2.1, относятся к классу обычных САУ.

Особой разновидностью САУ являются следящие системы, в которых задающее воздействие представляет собой неизвестную заранее функцию времени, связанную с внешним, по отношению к системе управления параметром, который может изменяться случайным образом, а целью управления является воспроизведение этого случайного закона управляемой величиной y (t) [1, 8-10]. Такие САУ применяются для управления одним технологическим параметром (ведомым) в зависимости от значения другого технологического параметра (ведущего), изменяющегося произвольно – например, управление расходом воздуха, подаваемого на горелку, в зависимости от расхода топлива; воспроизведение одним устройством перемещения другого устройства без механической связи между ними и т.п.

Пример следящей САУ соотношением расходов показан на рис. 18. Управляемым (ведомым) параметром является величина расхода F_{B рег} входного потока В на подаче в аппарат, регулирование которой осуществляется в заданном соотношении n с ведущим расходом – расходом потока А (см. рис. 18). Заметим, что в рассматриваемом примере величина соотношения n жестко задается функцией вычислительного устройства 3. В случае, если величина соотношения по условиям процесса может изменяться, используют регуляторы соотношения расходов с настраиваемой при помощи органов настройки регулятора величиной соотношения, или регуляторы с внешним заданием n [1].

Структурная схема САУ управления соотношением расходов по отклонению показана на рис. 19. В качестве задающего узла, формирующего задающее воздействие x (t) в зависимости от ведущего расхода F_А, изменяющегося случайным образом, выступают ТСА 2 и 3. Величина рассогласования, вычисляемая по цепи обратной связи, равна:

.

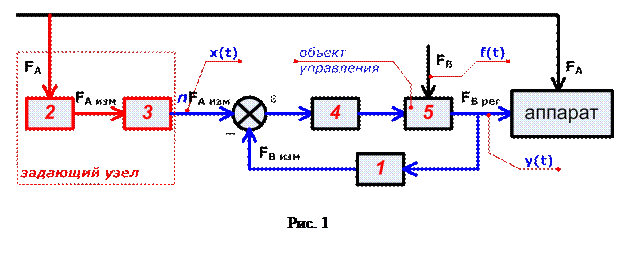
Следящие системы управления, так же как и обычные САУ, могут быть реализованы с использованием любого из принципов управления или их комбинации [1, 8-10]. Рассмотренный пример (см. рис. 18 и рис. 19) представляет собой систему, реализованную по принципу обратной связи (управление по отклонению).

Рассмотрим пример следящей САУ, реализующей комбинированное управление, на примере схемы автоматизации хлорирования воды (рис. 20). Целью управления является регулирование подачи хлора (ведомый параметр) в зависимости от изменяющегося расхода поступающей на хлорирование воды (ведущий параметр). Заданное соотношение расходов обеспечивается регулятором 7, который изменяет положение регулирующего клапана, установленного на линии подачи хлора из дозатора в эжектор. Признаком реализации рассматриваемой САУ по комбинированному варианту является использование в контуре управления контроля возмущения – измерения концентрации остаточного хлора в обработанной воде. Доза подаваемого хлора, определенная соотношением расходов, корректируется регулятором 7 в зависимости от остаточной концентрации.

Кроме контура управления в схеме, приведенной на рис. 20, реализован автоматический контроль давления воды в подающем трубопроводе (датчик 1 и преобразователь 2) с индикацией текущих показаний и световой сигнализацией при достижении давлением нижнего допустимого предела (прибор 3) [2, 18].

2.2.2. По принципу формирования сигналов управления

По принципу формирования сигналов управления различают следующие разновидности САУ [1, 8]:

1) САУ с непрерывным (аналоговым) управлением, в которых сигналы управления x (t), e(t) или z (t) представляют собой непрерывную функцию времени (рис. 21– а) и на любом ограниченном временном интервале могут иметь неограниченное число состояний;

2) САУ с дискретным управлением, в которых сигнал управления на любом ограниченном временном интервале может иметь конечное, фиксированное число состояний.

Для источников аналоговых сигналов характерна бóльшая, чем у дискретных, чувствительность к помехам и инструментальным погрешностям преобразователей (дрейф нуля, температурные колебания коэффициентов усиления и т.п.). Источники дискретных сигналов лишены этих недостатков, так как образующие их элементы работают не в усилительном, а в релейном режиме, поэтому дискретные сигналы обеспечивают бóльшую надежность при передачи на большие расстояния.

САУ с дискретным управлением делятся на цифровые, импульсные и релейные.

В цифровых САУ используется дискретное преобразование первичного непрерывного сигнала, которое называется квантованием по уровню, и сводится к замене бесконечного числа исходных значений конечным числом уровней (рис. 21– б). Разность уровней называется шагом квантования по уровню D s. Пока значение исходного непрерывного сигнала не изменится на величину, равную шагу квантования, преобразователь фиксирует предыдущее значение уровня. Разрядность современных цифровых устройств позволяет использование столь малых значений шага квантования по уровню, что погрешности такого представления становятся пренебрежимо малыми. После квантования цифровой сигнал подвергается кодированию – значение каждой величины уровня выражается цифровым кодом (числом). В цифровых САУ соответствующую форму обычно имеют задающее воздействие x (t), и, после преобразования, сигналы в обратных связях. Цифровой сигнал рассогласования e(t) может быть преобразован в непрерывное управляющее воздействие z (t).

В импульсных САУ используется квантование по времени – замена бесконечного числа значений исходного непрерывного сигнала конечным числом его значений, фиксируемых через определенный промежуток времени D t – шаг квантования по времени (рис. – а). В зависимости от того, какая характеристика последовательности – амплитуда импульсов (см. рис. – а), частота следования импульсов (рис. – б) или ширина импульсов (рис. 23– а) – пропорциональна величине входного сигнала, различают типы модуляции импульсных сигналов.

В релейных САУ управляющее воздействие формируется с использованием релейных регуляторов, у которых при непрерывном изменении входной величины регулирующий орган занимает ограниченное число положений. На рис. 23– б приведена характеристика двухпозиционного регулятора с зоной неоднозначности, у которого в зависимости от величины непрерывно изменяющегося задающего воздействия x (t) регулирующий орган занимает одно из двух возможных положений, определяемых двумя значениями управляющего воздействия – z_max и z_min. У такого регулятора, в зависимости от знака и величины задающего воздействия, регулирующий орган или полностью открыт (приток вещества или энергии максимальный), или полностью закрыт (приток вещества или энергии равен нулю). Примерами двухпозиционных устройств являются электроконтактный термометр, пневматическое реле и т.п.

В практике управления сложными объектами ТГВ непрерывное и дискретное управление используют совместно [1, 2, 10, 16].

2.2.3. По числу контуров управления

Данный классификационный признак характеризует структурную сложность САУ. В соответствии с ним САУ делятся на одноконтурные и многоконтурные [1].

В одноконтурных САУ управляющее воздействие является функцией единственного контролируемого параметра – управляемой величины в САУ по отклонению или возмущения в САУ по возмущению. Соответственно структура САУ имеет единственный контур общей обратной связи или контур компенсации.

Многоконтурные САУ имеют несколько независимых или связанных контуров управления, реализованных, например, с использованием местных обратных связей по параметрам, реагирующим на изменение управляющих воздействий быстрее, чем управляемая величина. Использование многоконтурного связанного регулирования позволяет улучшить качественные характеристики управления. Пример многоконтурной САУ приведен на рис. 16.

2.2.4. По характеру зависимости управляемых переменных от входных воздействий

По названному характеру зависимости САУ делятся на линейные и нелинейные.

Строго говоря, все практически реализуемые системы являются нелинейными. Однако, во многих случаях нелинейность рабочей характеристики системы является несущественной, и система может рассматриваться как линейная. Пример несущественно нелинейной характеристики САУ с линейной аппроксимацией в ограниченной области рабочей точки показана на рис. 24– а.

В системах, обладающих существенной нелинейностью, для достижения требуемого качества управления необходимо учитывать нелинейность объекта управления и использовать нелинейные управляющие устройства. Нелинейные характеристики могут быть неоднозначными, если при увеличении входного сигнала выходная величина изменяется по одной зависимости, а при уменьшении входного сигнала – по другой. Пример неоднозначной нелинейной характеристики кусочно-линейного типа для релейного элемента САУ показан на рис. 23– б, а примеры гладких нелинейных характеристик – однозначной и неоднозначной, приведены на
рис. 24– б и рис. 24– в соответственно. Заметим, что характеристику вида, приведенного на рис. 24– б, следует относить к существенно нелинейным только в том случае, если по условиям работы САУ она используется на всем своем протяжении. Например, такую форму зависимости носит величина рН от расхода реагента, ее регулирующего.

Для существенно нелинейных систем характерна работа в режимах, неосуществимых в линейных системах: автоколебания, дискретные изменения сигналов и т.д. [8, 10]

2.2.5. По характеру изменения ошибки управления

Данный признак классификации характеризует различия результатов работы САУ в установившемся состоянии, после завершения переходного процесса. По характеру изменения ошибки управления (отклонения управляемой величины от заданного значения) различают статические и астатические САУ.

У статических САУ при постоянном задающем воздействии ошибка управления стремиться к постоянному значению, зависящему от величины возмущения, т.е. после завершения переходного процесса имеет место статическая ошибка управления.

Для характеристик работы статической САУ (рис. 25) выполняется следующее:

,

где x ₀ – постоянная величина (модуль) задающего воздействия после его ступенчатого изменения в момент времени t ₀.

Как уже отмечалось, инерционность ТСА и ОУ обычно существенно больше, чем у источников задающих воздействий, поэтому, после изменения задающего воздействия, которое можно приближенно считать близким к идеальной ступеньке, новое установившееся значение управляемой величины y (t) достигается плавно, за время переходного процесса t_p. За это же время динамическая ошибка управления D (t), имеющая максимальное значение в момент времени t ₀, убывает до конечного постоянного значения D_ст, определяемого величиной действующего возмущения (см. рис. 25):

При наличии возмущающих воздействий статические системы не могут точно стабилизировать управляемую величину. Разомкнутые САУ являются статическими в целом, по отношению к любым возмущениям. Системы управления по возмущению являются статическим по отношению к возмущениям, для которых не предусмотрен контур компенсации.

У астатических САУ при постоянном задающем воздействии с течением времени переходного процесса ошибка управления стремиться к нулю вне зависимости от величины возмущения, т.е. после завершения переходного процесса статическая ошибка управления отсутствует.

Для характеристик работы астатической САУ (рис. 26) выполняется следующее:

Системы управления по отклонению являются астатическими в целом, т.е. при действии любых возмущений, последствие действия которых на объект управления может быть ликвидировано управляющим воздействием, после завершения переходного процесса статическая ошибка управления будет равна нулю. Комбинированные системы также являются астатическими в целом. Системы управления по возмущению обладают астатизмом только по отношению к возмущающему воздействию, для которого реализован контур компенсации.

Полная схема классификации систем автоматического управления по всем рассмотренным признакам приведена на рис. 27.

2.3.1. Модели статики и динамики САУ

Оценка качества функционирования САУ основана на исследовании статических и динамических характеристик.

Статическими называются характеристики, отображающие связь между входными воздействиями и управляемыми величинами в установившемся режиме, при котором входные воздействия и управляемые величины не изменяются. Если управляемая величина изменяется, т.е. переходной процесс в САУ еще не завершен, то состояние системы будет неустановившимся. Режим работы САУ при этом называют динамическим.

Для исследования статических и динамических характеристик САУ используют математические модели, имеющие вид уравнений связи между входными воздействиями и управляемыми величинами.

Дифференциальные уравнения описывают функционирование САУ в динамическом режиме и называются уравнениями динамики. При составлении уравнений динамики САУ разбивают на отдельные элементы – звенья, и записывают уравнение каждого звена в отдельности. Уравнение звена выражает зависимость между теми величинами на входе и выходе данного звена, то есть между величинами, представляющими воздействие предыдущего звена на данное и воздействие данного звена на последующее звено. Уравнения всех звеньев образуют систему уравнений, из которой можно получить уравнение САУ в целом путем исключения промежуточных переменных.

Алгебраические уравнения, описывающее установившийся режим, получаются из модели динамики САУ для случая, когда входные воздействия и управляемые величины не изменяются, и, соответственно, их производные равны нулю. Такие уравнения называют уравнениями статики.

Рассмотрим произвольное звено САУ (рис. 28). На вход звена поступает входное воздействие x (t). Звено в процессе функционирования формирует на выходе выходную величину y (t) в условиях действия внешнего возмущения f (t). В общем случае дифференциальное уравнение звена имеет нелинейный вид, т.е. переменные x (t), y (t) и f (t), а также их производные разных порядков могут входить в уравнение в виде аргумента степенных, показательных, логарифмических и других нелинейный функций:

F ₁(x, x '… x ^(m), y, y '… y ⁽ⁿ⁾) = F ₂(f, f '… f ^(k)).

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом процессе переменные изменяются так, что их отклонения от установившихся значений остаются все время достаточно малыми. Это условие для звена САУ и САУ в целом выполняется в отношении входной и выходной величин, поскольку этого требует сама идея работы САУ: система все время стремится свести к минимуму отклонения выходных величин от их заданных значений.

Но в отношении возмущения f (t) условие малости отклонений не выполняется, т.к. возмущения имеют случайную природу и их отклонения от номинального значения могут быть сколь угодно большими. Поэтому правая часть уравнения звена САУ линеаризации не подлежит и при линеаризации ее приравнивают к нулю:

F ₁(x, x '… x ^(m), y, y '… y ⁽ⁿ⁾) = 0.

Важно! Т.о. линеаризованные модели САУ являются приближенными и описывают функционирование систем и их звеньев в отсутствии помех и возмущений. Сфера их применения ограничена начальным этапом проектирования САУ. Исключение составляют модели систем, реализованных по принципу управления по возмущению или комбинированных систем: возмущения, влияние которых компенсируется системой, относят к входным воздействиям, подлежащим линеаризации.

Геометрически линеаризация является заменой реальной нелинейной характеристики звена САУ или САУ в целом на линейную. Рассмотрим линеаризацию характеристики звена САУ на примере проточного бака со свободным истечением жидкости (рис. 29– а), где F_вх – объемный расход поступающей в бак жидкости (приток); F_вых – объемный расход жидкости на выходе из бака (сток); L – уровень жидкости в баке.

Величина объемного расхода на линии стока определяется уровнем жидкости в баке, и эта зависимость имеет нелинейный вид:

,

(1)

где a – коэффициент, зависящий от гидравлического сопротивления и площади поперечного сечения выходного патрубка. При небольших изменениях расхода величину a можно считать постоянной.

Выберем на графике нелинейной зависимости F_вых = f (L) рабочую точку с координатами (L ₀, F_{вых 0}), соответствующую заданному (номинальному) режиму работы проточного бака (рис. 29– б). Поскольку по логике работы САУ будет стремиться свести к нулю отклонения L и F_вых от номинального режима, то в малых окрестностях рабочей точки исходную нелинейную характеристику можно заменить на линеаризованную – касательную. Линеаризованные характеристики САУ принято рассматривать не в координатных осях абсолютных значений переменных, а в координатных осях их отклонений от номинальных значений (см. рис. 29– б). Линеаризованная модель проточного бака, записанная для отклонений, имеет вид:

.

(2)

Рассмотренные нелинейная (1) и линеаризованная модели проточного бака (2), приведенные на рис. 29– б, описывают зависимости между установившимися значениями входной и выходной переменных, т.е. являются моделями статики. Линеаризованную модель динамики получают разложением непрерывной функции F_вых = f (L), дифференцируемой в окрестностях точки (L ₀, F_{вых 0}), в ряд Тейлора, с ограничением его линейными членами.

В общем виде линеаризованное дифференциальное уравнение (модель динамики) отдельного звена САУ или системы в целом имеет вид:

(3)

где x (t) – входное воздействие звена (системы); y (t) – выходная величина звена (системы); a_i и b_j – постоянные коэффициенты, определяемые физическими параметрами звена (системы).

Важно! Обратите внимание на то, что уравнение (3) имеет линейную форму: переменные x (t) и y (t), а также их производные по n -ый и m -ый порядок соответственно, входят в уравнение в первой степени, т.е. не являются аргументами нелинейных функций.

Модель статики звена (системы) получается из модели динамики (3) при x (t)=const и y (t) = const. В этом случае производные входного и выходного параметров равны 0:

и, следовательно, модель статики принимает вид:

где k – коэффициент статического преобразования звена (системы) [1, 10, 13].

Модели динамики звеньев САУ в виде (3) получают экспериментальным или теоретическим способом.

При экспериментальном получении моделей динамики используют следующий алгоритм:

- на вход реального устройства (ТСА) подают сгенерированное ступенчатое воздействие x (t);

- с выхода устройства прямым измерением получают график зависимости y (t), т.е. экспериментальную кривую переходного процесса;

- подбирают аналитическую функцию, описывающую кривую переходного процесса y (t);

- подбирают линейное дифференциальное уравнение, аналитическая форма решения которого совпадает с найденной функцией y (t).

В теоретическом способе модель динамики звена САУ в виде (3) получают с использованием известных теоретических описаний процессов функционирования звена.

Осуществим вывод модели динамики проточного бака. Целью вывода модели динамики является дифференциальное уравнения вида (1), связывающее входную и выходную величины звена, которыми для проточного бака являются F_вх (t) и F_вых (t). Известным теоретическим описанием процесса функционирования бака является уравнение его материального баланса:

,

где V – объем жидкости в баке, который через постоянную площадь сечения бака А и переменный уровень жидкости в баке L определяется как:

,

т.е. уравнение материального баланса принимает вид:

.

Выразим величину уровня через объемный расход на стоке из бака, воспользовавшись нелинейной моделью статики бака (1):

,

и подставим в уравнение матбаланса:

,

.

Т.о., в общем виде модель динамики проточного бака можно записать как:

.

(4)

Важно! Обратите внимание на то, что уравнение (4) имеет нелинейную форму: первая производная в левой части уравнения вычисляется от второй степени выходной величины , т.е. от нелинейной функции. Такой результат получился из-за того, что при выражении уровня L через объемный расход стока мы воспользовались нелинейной статической характеристикой проточного бака (1).

Однако, в практических задачах анализа САУ используют линеаризованные модели динамики вида (3). Осуществим вывод линеаризованной модели динамики проточного бака с использованием полученной ранее линеаризованной модели статики (2), рассматриваемой в координатных осях отклонений (см. рис. 29– б). Выразим величину отклонения уровня через отклонение расхода стока:

,

и подставим в уравнение матбаланса, записав его для отклонений:

,

.

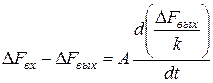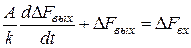При записи линеаризованных уравнений динамики знак отклонений обычно опускают, т.о. модель динамики бака принимает вид [1, 10, 16]:

.

Т.о., в общем виде линеаризованную модель динамики проточного бака можно записать как:

, .

(5)

Важно! Обратите внимание на то, что уравнение (5) имеет линейную форму и соответствует общему виду линеаризованной модели произвольного звена или САУ (1), для которого n =1, m =0, а ₁=t, а ₀=1, b ₀=1.

Сравним точность анализа поведения проточного бака при изменение входного расхода (притока) полученного с использованием нелинейной (4) и линеаризованной (5) моделей динамики. Пусть имеется бак со следующими характеристиками: A = 1 м², a=1, k =0,707. Пусть до момента времени t ₀ в баке имело место установившееся состояние равновесия:

F_вх = F_вых = 0,2 м³/с.

Пусть в момент времени t ₀ расход притока скачком возрастает до величины 0,5 м³/с. Численное решение в заданных условиях уравнений (4) и (5) относительно F_вых (t) позволяет получить график изменения F_вых (t) с момента времени t ₀ и до момента восстановления равновесия, т.е. до момента времени, когда значение стока сравняется с новым значением притока:

F_вх = F_вых = 0,5 м³/с.

Графики изменения F_вых (t) с момента времени t ₀, полученные с использованием моделей (4) и (5), приведены на рис. 30. Как видно, погрешность анализа, выполненного с использованием линеаризованной модели (5) относительно точного результата, полученного по модели (4), пренебрежимо мала. Следовательно, применение упрощенных линеаризованных моделей для анализа динами САУ оправдано.

2.3.2. Модельные режимы анализа САУ. Качество процесса управления

Математические модели САУ, рассмотренные в предыдущем параграфе, используют для анализа качественных характеристик управления на стадии проектирования САУ. Поскольку заранее неизвестно, каким в реальных условиях будет задающее воздействие, при анализе качества используют типовые модельные тестовые воздействия, по виду которых различают модельные режимы анализа. К типовым тестовым воздействиям относятся ступенчатое, гармоническое, линейно-возрастающее и др.

Реакция САУ на ступенчатое воздействие наиболее показательна, т.к. в процессе управления системы подвергаются внешним воздействиям, очень близким к ступенчатым. Поэтому для анализа САУ ступенчатое воздействие используют в первую очередь.

Пусть на САУ, находящуюся в установившемся режиме, в момент времени t ₀ воздействует ступенчатое воздействие вида:

где х ₀ = const – модуль ступенчатого воздействия. До момента времени t ₀ воздействие x (t) равно нулю, следовательно такой режим исследует запуск работы САУ с заданием начального значения задающего воздействия, равного х ₀. Закон изменения управляемой величины y (t), т.е. форма и длительность переходного процесса, определяется динамическими свойствами САУ – порядком дифференциального уравнения САУ и значениями его коэффициентов, а также величиной х ₀. Кривую переходного процесса можно получить экспериментально или построить, решив дифференциальное уравнение САУ (1) и построив график решения.

Примеры переходных процессов различных форм с одинаковой длительностью t_p приведены на рис. 31. Предпочтительным является монотонный переходной процесс экспоненциальной формы: он обеспечивает максимальную скорость убывания динамической ошибки управления. Наименее желательной является колебательная форма, т.к. в таком переходном процессе имеют место отклонения выходной величины y (t) от конечного значения как со знаком «плюс», так и со знаком «минус».

Закон изменения y (t) после приложения ступенчатого воздействия (для t ³ t ₀) можно представить в виде суммы двух составляющих: переход­ной y_п (t) и вынужденной y_в (t):

y (t) = y_п (t) + y_в (t), t ³ t ₀.

Переходная составляющая устойчивой системы с течением времени переходного процесса затухает (стремится к нулю) и система приходит в новый установившийся режим, характеризуемый конечным значением вынужденной состав­ляющей y _¥ (см. рис. 31):

для t ³ t ₀ при t ® ¥, y_п (t) ® 0,

y_в (t) ® y _¥ = const.

Если САУ является астатической и после завершения переходного процесса обеспечивает строгое равенство выходной величины заданному значению (т.е. отсутствие статической ошибки управления), то:

y_в (t) ® y _¥ = const = k×x ₀,

где k – коэффициент статического преобразования САУ.

Как видно (см. рис. 31) при подаче ступенчатого воздействия система переходит из одного установившегося режима (до момента времени t ₀) в другой (после момента времени t ₀+ t_p), через динамический режим переходного процесса.

Ступенчатое воздействие, модуль которого х ₀ = 1 называется единичным скачком и обозначается 1(t):

График изменения y (t), полученный при подаче на вход САУ единичного скачка, называется переходной характеристикой САУ. Переходная характеристика может быть получена экспериментально или решением уравнения (1). В отсутствии статической ошибки управления переходная характеристика сходится к значению, равному коэффициенту статического преобразования САУ:

y_в (t) ® y _¥ = y_зд = k.

По переходной характеристике определяют ряд показателей качества управления.

К показателям быстродействия относят:

- время переходного процесса САУ t_p – время, начиная с которого y (t) не отличается от нового установившегося значения более чем на величину d (d£0,05× y _¥), т.е. при (рис. 32);

- время установления САУ t_у – время достижения переходной характеристикой первого максимума (определяется только для переходных процессов колебательного вида, см. рис. 32).

Точность управления определяется разницей между заданным и текущим значением управляемой величины, т.е. ошибкой управления:

Основным показателем точности управления является статическая ошибка управления D_ст (см. рис. 32):

Как уже отмечалось, колебательная форма переходного процесса является наименее желательной. В качестве дополнительных показателей качества управления для нее используют:

- перерегулирование Н _max – относительную величину максимального «выброса» переходной характеристики (см. рис. 32):

- колебательность переходной характеристики САУ n – число полных колебаний характеристики за время t_p.

Все показатели качества управления САУ, определяемые по переходной характеристике, должны иметь минимально возможные значения.

К основным модельным тестовым воздействиям анализа САУ относится также гармонический сигнал вида:

где А_вх – амплитуда входного сигнала; w – частота входного сигнала. Если задающее воздействие САУ имеет гармонический вид, то на выходе устойчивой системы, после затухания свободных колебаний (переходной составляющей), установятся вынужденные колебания с той же частотой w, но отличающиеся амплитудой и сдвигом фазы (рис. 33):

y (t) = y_п (t) + y_в (t), t ³ t ₀,

для t ³ t ₀ при t ® ¥, y_п (t) ® 0,

y_в (t) ® .

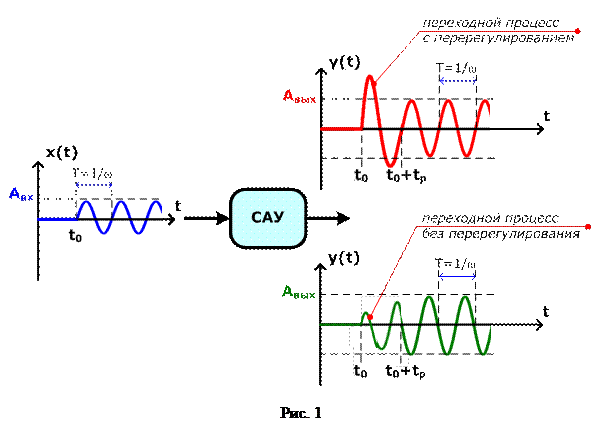
Состояние САУ, в котором после завершения переходного процесса амплитуда выходной величины А_вых и сдвиг фазы j _вых больше не изменяются (см. на рис. 33 с момента времени t ₀+ t_p), является установившимся состоянием особого вида, которое называется стационарным режимом колебаний. Важной особенностью этого режима является то, что ослабление или усиление амплитуды выходной величины по сравнению с входной A_вых / A_вх и сдвиг фазы j _вых не являются постоянными для конкретной САУ, а зависят от частоты входного воздействия w. Исследование этих зависимостей относится к задачам частотного анализа САУ и позволяет предсказать поведение реальной системы в условиях действия реальных входных воздействий периодического вида.

Наличие сдвига фазы выходного гармонического сигнала относительно входного объясняется инерционностью САУ. По сути, сдвиг фазы является временной задержкой выходного сигнала, обусловленной конечной длительностью переходного процесса. Однако, поскольку эта величина является аргументом функции синуса, она должна выражаться в радианах или градусах, а не в единицах измерения времени. При этом величину задержки по времени выходного сигнала относительно входного t можно рассчитать с учетом того, что фаза гармонического сигнала за время периода изменяется на 360°:

,

где T = 1/w – период гармонического сигнала.

Пример работы САУ при подаче гармонического воздействия показан на рис. 34. С момента времени t ₀ задающее воздействие САУ x (t) начинает изменяться по гармоническому закону, что вызывает переход системы в режим переходного процесса, за время которого амплитуда колебаний y (t) плавно возрастает, пока не достигнет конечного постоянного (стационарного) значения А_вых. С этого момента система работает в стационарном режиме колебаний.

В частотной зависимости характеристик САУ можно убедиться, сравнив рис. 34 с примером работы той же САУ при подаче воздействия с бóльшей частотой (рис. 35). Как видно, для нового значения частоты стационарное значение амплитуды колебаний y (t) А_вых меньше, чем на рис. 34, а задержка по времени t (и, соответственно, сдвиг фазы j _вых) – бóльше. Кроме того, в переходном процессе имеет место перерегулирование – превышение амплитудой y (t) конечного стационарного значения: А_{вых max} > А_вых.

Линейно возрастающе е тестовое воздействие вида x (t) = a× t, где a – постоянный коэффициент, преимущественно применяется при исследовании динамики следящих систем.

Основные задачи анализа, решаемые при про­ектировании САУ делятся на:

- задачу анализа статических состояний;

- задачу анализа переходной характеристики (анализ функционирования САУ при подаче на вход единичной ступеньки);

- задачу анализа частотных характеристик (анализ функционирования САУ при подаче на вход гармонических воздействий);

- задачу анализ устойчивости.

Анализ статических состояний относится к задачам стати­ки, а остальные виды анализа – к задачам динамики.

Устойчивостью называют свойство системы самостоятельно приходить к установившемуся режиму после приложения входного воздействия, которое вывело ее из состояния равновесия. Исследование устойчивости является одной из основных задач в теории автоматического управления.

Как уже отмечалось, процесс управления определяется переходным процессом: законом изменения y (t) после изменения любого из входных воздействий. Переходной процесс САУ в заданных условиях можно получить решением дифференциального уравнения САУ, которое может быть представлено как сумма двух составляющих, вынужденной у_в (t) и переходной y_п (t):

y (t)= у_в (t)+ y_п (t),

где y_в (t) определяется свойствами системы и видом входного воздействия. САУ будет устойчивой, если с течением времени переходная составляющая будет стремиться к нулю:

и неустойчивой, если с течением времени переходная составляющая будет стремиться к бесконечности:

Однозначно судить об устойчивости системы можно по виду ее переходной характеристики: затухающая переходная характеристика (сходящаяся к некоторой постоянной) соответствует устойчивой системе, расходящаяся – неустойчивой [1, 2, 8, 10, 13].

Примеры переходных характеристик устойчивых систем показаны на рис. 31, а примеры переходных характеристик неустойчивых систем – на рис. 36. Как очевидно следует из формы характеристик на рис. 36, неустойчивые системы неработоспособны: они не обеспечивают стабилизацию управляемой величины на заданном значении, определяемом величиной входной ступеньки х ₀.

Дата добавления: 2014-01-04