Методы исследования

Системы линейных уравнений общего вида

Напомни, что и называются базисными неизвестными.

Здесь С1 и С2 произвольные константы.

.

Таким образом, общее решение исходной системы имеет вид

Используя это значение, из первого уравнения выразим через и.

.

Для заметок

Решение, полученное из общего при С₁ = С₂ =0 называют базисным решением. Если при этом базисные неизвестные неотрицательны, то такое решение называют опорным.

Если система (5.1) оказалась совместной, т. е. матрицы A и 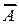имеют один и тот же ранг, т.е.

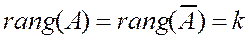
то могут представиться две возможности - a) k = n; б) k < n:

а) если k = n, то имеем n независимых уравнений с n неизвестными, причем определитель Δ этой системы отличен от нуля. Такая система имеет единственное решение, получаемое по формулам Крамера;

б) если k < n, то число независимых уравнений меньше числа неизвестных.

Перенесем лишние неизвестные x _r+1, x _r+2,..., x_n, которые принято называть свободными, в правые части; наша система линейных уравнений примет вид:

a₁₁ x₁ + a₁₂ x₂ +... + a_1k x_k = b₁ - a₁,_k+1 x_k+1 -... - a_1nx_n,

a₂₁ x₁ + a₂₂ x₂ +... + a_2k x_k = b₂ - a₂,_k+1 x_k+1 -... - a_2nx_n,

..............................

a_r1 x₁ + a_r2 x₂ +... + a_kk x_k = b_k – a_k,_k+1 x_k+1 -... – a_knx_n.

Ее можно решить относительно x₁, x₂,..., x_k, так как определитель этой системы (k-го порядка) отличен от нуля. Придавая свободным неизвестным произвольные числовые значения, получим по формулам Крамера соответствующие числовые значения для x₁, x₂,..., x_k. Таким образом, при k < n имеем бесчисленное множество решений.

Система (5.1) называется однородно й, если все b_i = 0, т. е. она имеет вид:

a ₁₁ x₁ + a₁₂ x₂ +... + a_1n x_n = 0,

a₂₁ x₁ + a₂₂ x₂ +... + a_2n x_n = 0, (9.1)

..................

a_m1 x₁ + a_m1 x₂ +... + a_mn x_n = 0.

Из теоремы Кронекера-Капелли следует, что она всегда совместна, так как добавление столбца из нулей не может повысить ранга матрицы. Это, впрочем, видно и непосредственно - система (9.1) заведомо обладает нулевым, или тривиальным, решением x₁ = x₂ =... = x_n = 0. Пусть матрица А системы (9.1) имеет ранг k.

Если k = n, то нулевое решение будет единственным решением системы (8.1); при k < n система обладает решениями, отличными от нулевого, и для их разыскания применяют тот же прием, как и в случае произвольной системы уравнений.

Дата добавления: 2014-01-04