
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доказательство теорем
Формулировка теоремs о линейной зависимости четырех векторов.
Теорема 16.3: 4 вектора всегда линейно зависимы.
Доказательство теоремы 16.1:
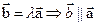 (Смотри п14.2(§14) правило 1) определение)
(Смотри п14.2(§14) правило 1) определение)
Если 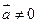 , то
, то
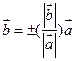 (“+”, если сонаправленны; “–“, если противоположно направлены).
(“+”, если сонаправленны; “–“, если противоположно направлены).
(читателю предлагаем самостоятельно доказать, что если 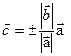 («+», если
(«+», если 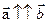 и «-» то
и «-» то 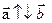 ), то
), то 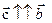 и
и 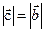 ) т.е
) т.е 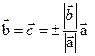 )
)
Причём, если 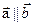 , то
, то 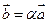 , и
, и 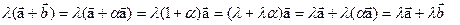 и, таким образом, свойство (5) суммы и умножения векторов на число (см.31.4) полностью доказано.
и, таким образом, свойство (5) суммы и умножения векторов на число (см.31.4) полностью доказано.
Доказательство теоремы 16.2:
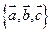 – л.з.
– л.з. 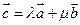 и они компланарны, ибо
и они компланарны, ибо 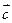 является диагональю параллелограмма, на сторонах которого лежат векторы
является диагональю параллелограмма, на сторонах которого лежат векторы  и
и  .(см. рис 16.1)
.(см. рис 16.1)



В
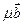
Пусть 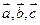 – компланарны;а
– компланарны;а  (иначе
(иначе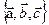
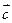
содержит линейно зависимую подсистему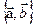
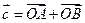




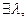
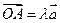 ;
; 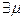 ,
, 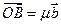 .
.
Тогда 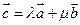 O
O 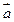
 A
A
Рис 16.1
Мы показали так же что справедлива
Лемма 16.1: если 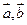 неколлинеарные,
неколлинеарные, 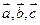 компланарные, то
компланарные, то  , что
, что 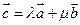 .
.
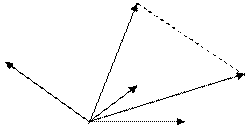
Доказательство теоремы 16.3:
Пусть 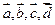 выходят из общего начала (точки О). Можно считать, что среди векторов
выходят из общего начала (точки О). Можно считать, что среди векторов 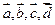 нет компланарных троек (иначе существует л.з. подсистема). Из конца вектора
нет компланарных троек (иначе существует л.з. подсистема). Из конца вектора  (т.D) проводим прямую до её пересечения с плоскостью, на которой расположены векторы
(т.D) проводим прямую до её пересечения с плоскостью, на которой расположены векторы  и
и  . Пусть М – искомая точка пересечения. (см. рис 16.2)
. Пусть М – искомая точка пересечения. (см. рис 16.2)
Тогда 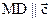 и, следовательно,
и, следовательно, 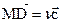 (16.1)
(16.1)
По правилу треугольника, 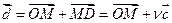 (16.2)
(16.2)
Векторы  и
и  не коллинеарные, и тогда
не коллинеарные, и тогда 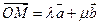 (16.3)
(16.3)
Подставляя вместо 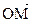 в (16.2) его выражение по формуле (16.3), получаем
в (16.2) его выражение по формуле (16.3), получаем 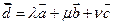 , т.е.
, т.е. 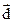 линейно выражается через векторы
линейно выражается через векторы 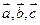 , и система
, и система 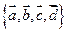 – л.з.
– л.з.
 |
D
C B M
O A
Рис 16.2
|
Дата добавления: 2014-01-04; Просмотров: 1403; Нарушение авторских прав?; Мы поможем в написании вашей работы!