
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Линейное пространство и линейные операторы
|
|
|
|
Эта система линейно независима;
2) любой вектор можно выразить через 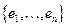 , причём это выражение единственно.
, причём это выражение единственно.
Доказательство:
Т.к. 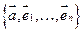 – линейно зависима, то
– линейно зависима, то 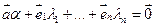 при
при 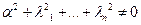 (17.1)
(17.1)
Если 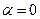 , то из (17.1) получим, что
, то из (17.1) получим, что 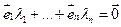 и
и 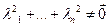 , т.е. система
, т.е. система 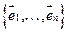 – линейно зависима, чего не может быть, т.к. она является базисом.
– линейно зависима, чего не может быть, т.к. она является базисом.
Поэтому 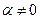 , и, поделив обе части (17.1) на
, и, поделив обе части (17.1) на 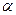 и перенося слагаемые
и перенося слагаемые 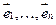 в правую часть, получим, что
в правую часть, получим, что 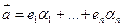 с
с 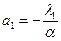 ;…;
;…;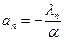 .
.
Получим единственность: 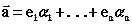 (17.2)
(17.2)
Если существует другое разложение (17.2): 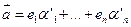 , (17.3)
, (17.3)
то, вычитая из (17.2) равенство (17.3), получим: 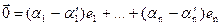
Но, так как система 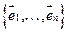 – л.нез., то мы получаем, что
– л.нез., то мы получаем, что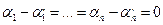 . т.е
. т.е
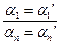
Единственность доказана. Доказана также следующая лемма.
Лемма 17.1: если система 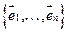 – л.нез., а
– л.нез., а 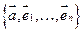 – л.з., то элемент “
– л.з., то элемент “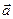 ” единственным образом линейно выражается через элементы
” единственным образом линейно выражается через элементы 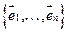 .
.
Определение: 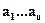 называются координатами вектора
называются координатами вектора 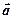 при его разложении по базису
при его разложении по базису 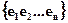
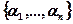 в (17.2)
в (17.2)
Теорема 17.2: При сложении векторов их координаты складываются, а при умножение вектора на число – координаты умножаются на это число.
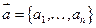 ;
; 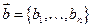
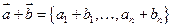
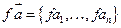
Доказательство:
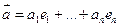 и
и 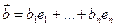 , тогда
, тогда 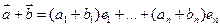 и
и 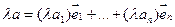
Определение: Линейное пространство над множеством вещественных чисел – некоторое множество объектов, где заданы операции сложения и умножения на действительное число, со следующими свойствами:
1) 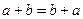
2) 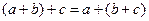
3) 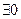
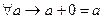
4) 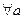
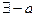
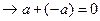 , тогда
, тогда 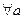
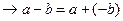
5) 
6) 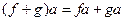
7) 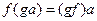
8) 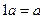

В линейном пространстве действуют все определения и теоремы §15 и §17.
Теорема 18.1: Система линейно зависима, когда хотя бы один из её элементов можно выразить через остальные.
Доказательство такое же, как и у векторов. Система линейно независима, если из того 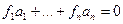 , что
, что 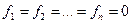 .(т.е содержит ненулевой элемент)
.(т.е содержит ненулевой элемент)
Определение18.1 Если в нетривиальном пространстве существует базис, то пространство называется конечномерным.
Определение18.2: Число элементов базиса – размерность линейного пространства.
Теорема 18.2: Все базисы одного и того же пространства состоят из одинакового количества элементов.
Теорема 18.2 будет доказана ниже (как следствие теоремы о замене элементов базиса).
Из неё, в частности, следует корректность определения размерности линейного пространства и её независимость от выбора базиса.
Определение 18.3: Линейной оболочкой 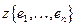 называется множество всех элементов линейного пространства, которые линейно выражаются через
называется множество всех элементов линейного пространства, которые линейно выражаются через 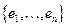 .
.
Определение18.4: Систему 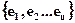 назовем полной, если все линейное пространство является ее линейной оболочкой т.о. Базис - полная линейно не зависимая система элементов.
назовем полной, если все линейное пространство является ее линейной оболочкой т.о. Базис - полная линейно не зависимая система элементов.
Теорема 18.3: Координаты суммы равны сумме координат. (доказывается аналогично теореме 17.2)
Теорема о замене элементов базиса:
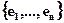 - базис (18.1)
- базис (18.1)
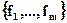 - линейно независимая система
- линейно независимая система 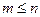 (18.2)
(18.2)
Тогда некоторые m элементы (18.1) заменяются на элементы (18.2)
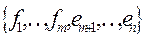 (18.3) (причём система (18.3) будет базисом)
(18.3) (причём система (18.3) будет базисом)
Согласно определениям §17, базис дополнить нельзя, ибо, любые его дополнения делают его линейно зависимой системой. т.е из теоремы 18.2 получается из теорема о замене элементов базиса.
Следствие18.1: Любую линейно независимую систему в конечномерном линейном пространстве можно дополнить до базиса.
Лемма 18.1:
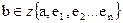
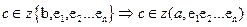
Доказательство леммы 18.1:
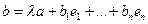 (18.4)
(18.4)
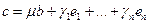 (18.5)
(18.5)
Подставляя в (18.5) вместо b его выражение из формулы (18.4), получим
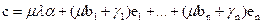 (18.6)
(18.6)
Лемма 18.2:
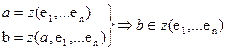 (18.7)
(18.7)
Доказательство:
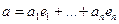 (18.8)
(18.8)
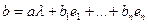 (18.9)
(18.9)
Поместив вместо a в (18.9) его выражение по формуле (18.8), получим:
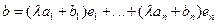
Следствие: Всякую полную систему можно уменьшить до базиса.
Доказательство теоремы о замене элементов базиса методом математической индукции:
m=1 (база индукции)
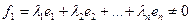 Тогда можно считать, что
Тогда можно считать, что 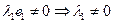
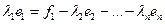
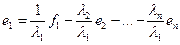
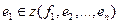 т.к. (18.1) – базис, то
т.к. (18.1) – базис, то 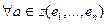 .
.
Тогда, по лемме 18.1 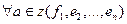 , т.е. система
, т.е. система 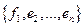 – полная.
– полная.
Допустим, что 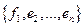 линейно зависима. Тогда по лемме 17.1
линейно зависима. Тогда по лемме 17.1 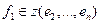
Но т.к.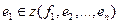 , то по лемме 18.2:
, то по лемме 18.2: 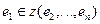 , и система
, и система 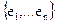 – л.з.
– л.з.
Следовательно, предположение о линейной зависимости системы 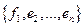 неверно.
неверно.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 751; Нарушение авторских прав?; Мы поможем в написании вашей работы!