Свойства векторного произведения .(антикоммутативность, линейность и однородность)

1. (антикоммутативность)

2. 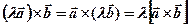(однородность)

3. и 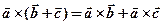(адютивность (линейность))

Доказательство свойств:

1)

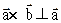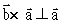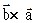
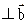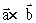Доказательство: и и , а так жет.е. и 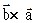ортогональны одним тем же плоскостям.

Поэтому 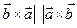и(это мы определяем по правилу правой руки) 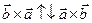, а 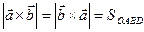(см. Рис25.1) следовательно

2)

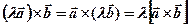
Доказательство: Рассмотрим следующие случаи ;;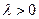

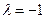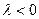
1) ,

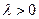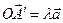
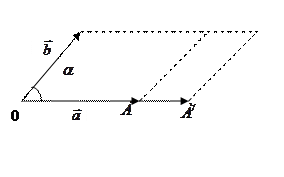
Рис 25.2

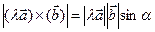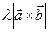=, а так как 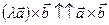, ибо они ортогональны плоскости параллелограмма OADB (см. рисунок 25.2), а так же они имеют одинаковое направление ,что можно определить направление по правилу правой руки то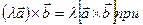 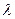>0

2)

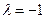
Рис 25.3

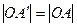(см. рис. 25.3)

(25.1),

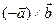ибо и 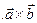ортогональны одной и той же плоскости параллелограмма OABD, 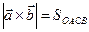(25.2)

(25.3)

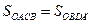, ибо эти параллелограммы имеют одинаковые стороны 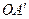и и общую высоту опущенную из вершины B. Поэтому из (25.2) и (25.3) следует , что:

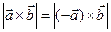
Читателю рекомендуем самостоятельно по правилу правой руки установить, то, что они направлены в разные стороны.

что 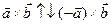и поэтому 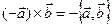и случай 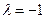доказан.

3)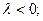тогда 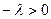,и для

можно применить случай 1). Из случаев 1)и 2) имеем:

(

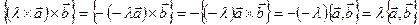
(*)Свойство2)Для второго множителя можно доказать , используя уже доказанную антикоммутативность ( Свойство1)и только что полученное свойство2) для первого множителя:

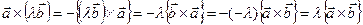
3) , Рассмотрим следующие случаи:

А),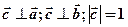

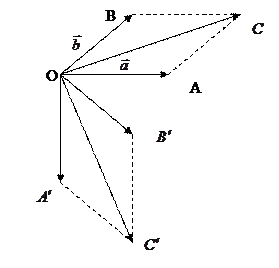
Рис 25.4

Пололожим 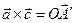, , ; аналогично

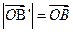(25.7)

Тогда сумма диагональ параллелограмма OACB (25.4)

(25.5)

Также 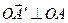: и 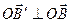по определению векторного произведения 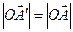, и и 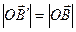(см 25.7)тогда параллелограмм 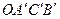получится из параллелограмма OACB поворотом последнего на угол 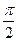( по часовой стрелке). Поэтому и диагональ

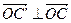и 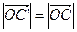=(напомним, что 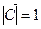и 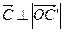, т.е.

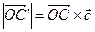(25.6)

Подставляя в (25.6) вместе 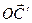и 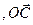их значения из формулы (25.4) и (25.6) получим

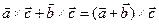
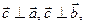
случай А) доказан

Б) 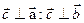введем вектор

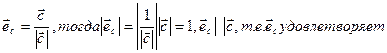
условию А) поэтому

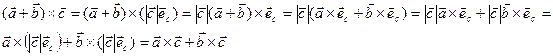
, и случай Б доказан

В дальнейшем случае нам понадобится Лемма25.1:

Обозначим за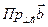проекцию вектора 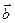на плоскость , перпендикулярную вектору 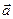(эта проекция сама является вектором, которая на рис 25.5 обозначим за ).

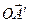Тогда имеет равенство:

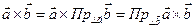(25.8)

Доказательство Леммы 25.1:

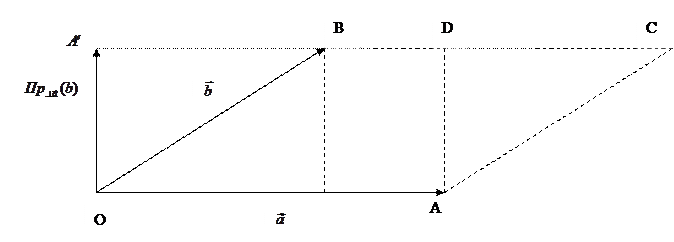
Рис 25.5

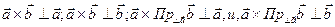( см. рис 25.5). Поэтому 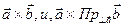ортогональна той же плоскости параллелограмма OACB (см. рис 25.5 где вектор 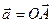). Поэтому они коллинеарные и по правилу правой руки определяем ,что

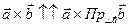(25.9)

Их длины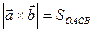(25.10)

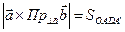(25.11)

Но параллелограмм OACB и прямоугольник 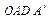имеет одинаковые площади, ибо они имеют общую сторону OA и одинаковую высоту( эта высота равна AD).

Поэтому из (25.10) и (25.11) получаем , что

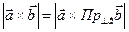(25.12)

Тогда из (25.12) и (25.9) получим , что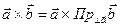

Для доказательства правой части (25.8) можно использовать антикоммутативность и только что полученное равенство.

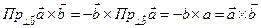
Лемма 25.1 доказана.

Продолжим доказательство свойства 3

В) Так как 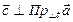и 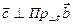, то вектора , и 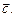удовлетворяют уже доказанному свойству Б. А так как проекция суммы равна сумме проекций( это было доказано в §20), т.е из Леммы 25.1 получим :

Для доказательства равенства 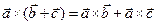используем антикоммутативность векторного произведения и только что доказанное равенство:

.

Свойство 3 полностью доказано.

Дата добавления: 2014-01-04; Просмотров: 1345; Нарушение авторских прав?; Мы поможем в написании вашей работы!