Векторное поле и криволинейный интеграл (КИ). Свойства КИ

Учебное пособие

Вегетотропные средства

Учебное издание

Составители:

Левента Алексей Иванович

Куклина Людмила Борисовна

Шапкин Юрий Григорьевич

Тираж 40 экз. Гарнитура Times New Roman.

Бумага офсетная. Печать ризография.

Усл. печ. л. 1,38.

Известно

Линия в координатном пространстве R³ задается (одно) параметрическим уравнением

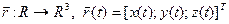
è Прямая в R³задается параметрическим уравнением:

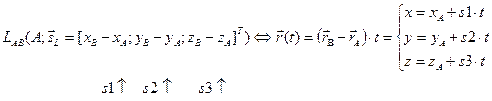
Утверждение. Линия в координатном пространстве R³ задается (одно) параметрическим уравнением

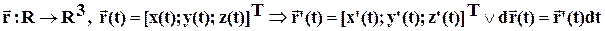
è Линия пересечения поверхностей:

è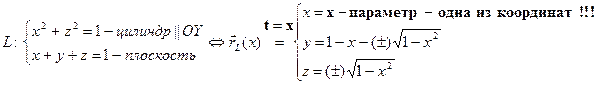

---------------------------------------------------------------------------------------

Пусть в R³ определены: 1) непрерывное векторное поле F(r), заданное векторной функцией трех переменных

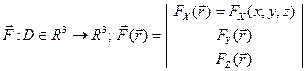(1)

2) гладкая линия 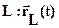, заданная (одно)параметрическим уравнением 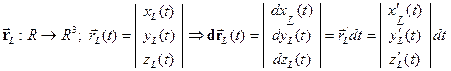(2)

3) точки А, В, лежащие на линии L: 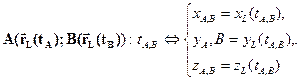(3)

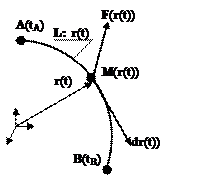Очевидно, что в точках линии L

(1) векторное поле F задается векторной функцией одной переменной

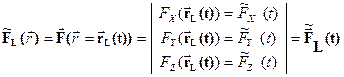
(2) скалярное произведение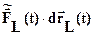

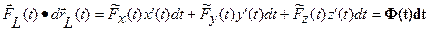
определяется скалярной функцией Ф(t) одной переменной - параметра “t” уравнения гладкой линии.

Определение. Криволинейным интегралом (II рода) от векторного поля F(r) вдоль гладкой линии L: 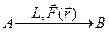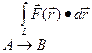называют число, равное интегралу

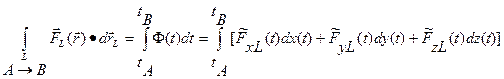(4)

Утверждение (т. существования). Криволинейный интеграл существует, если векторное поле непрерывно вдоль кусочно - гладкой линии L.

Из определения КИ следуют

свойства криволинейного интеграла (КИ) второго рода:

1) Линейность:

2) Аддитивность: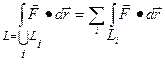

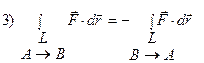
4) В общем случае, КИ в векторном поле зависит от начальной и конечной точек «пути» и от «формы пути» L

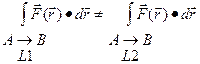
Замечание. Так как скалярное произведение векторов F (t)d r (t)= || F || ||d r ||cos( F,r ), для силового поля F криволинейный интеграл равен работе по перемещению материальной точки из точки А в точку В по линии L в поле силы F.

Дата добавления: 2014-01-04