Одновременность событий в разных системах отсчета

Следствия из преобразований Лоренца

Я лекция. Разные системы отсчета

Длина тела в разных системах отсчета. Промежуток времени между событиями. Собственное время. Инвариантность интервала. Времениподобные и пространственноподобные интервалы. Преобразование скоростей.

Из преобразований Лоренца вытекает ряд необычных с точки зрения классической механики следствий.

Пусть в системе К в точках с координатами х ₁ и х ₂ происходят одновременно два события в момент времени t ₁ = t ₂ = b. Согласно формулам (37,11) в системе K’ этим событиям будут соответствовать координаты

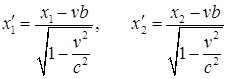
и моменты времени

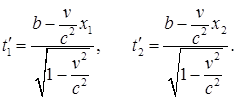
Из написанных формул видно, что в случае, если события в системе К происходят в одном и том же месте пространства (x ₁ = х ₂), то они будут совпадать в пространстве (х ₁' = x ₂') и во времени (t ₁' = t ₂') также и в системе К '. Если же события в системе К пространственно разобщены (х ₁ /= x ₂), то в системе К ' они также окажутся пространственно разобщенными (х ₁' /= x ₂'), но не будут одновременными (t ₁' /= t ₂'). Знак разности t ₂' — t ₁' определяется знаком выражения v (x ₁ — x ₂); следовательно, в разных системах К ' (при разных v) разность t ₂' — t ₁' будет различна по величине и может отличаться по знаку.

Это означает, что в одних системах событие 1 будет предшествовать событию 2, в других системах, наоборот, событие 2 будет предшествовать событию 1. Заметим, что сказанное относится лишь к событиям, между которыми отсутствует причинная связь.

Причинно связанные события (например, выстрел и попадание пули в мишень) ни в одной из систем отсчета не будут одновременными и во всех системах событие, являющееся причиной, будет предшествовать следствию. Подробнее об этом будет речь в следующем параграфе.

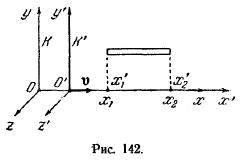
Длина тел в разных системах. Рассмотрим стержень, расположенный вдоль оси х и покоящийся относительно системы отсчета К ' (рис. 142). Длина его в этой системе

равна l ₀ = х '₂ — х '₁,,где х '₂ и х '₁— не изменяющиеся со временем t ' координаты концов стержня. Относительно системы К стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня х ₂ и х ₁ в один и тот же момент времени t ₁ = t ₂ = b. Их разность l = х ₂ — х ₁ даст длину стержня, измеренную в системе К. Чтобы найти соотношение между l ₀ и l, следует взять ту из формул преобразований Лоренца, которая содержит х ', х и t, т. е. первую из формул {37.11). Согласно этой формуле

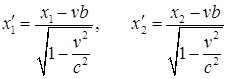
Откуда

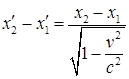
или окончательно

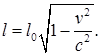(38.1)

Таким образом, длина стержня l, измеренная в системе, относительно которой он движется, оказывается меньше длины l ₀, измеренной в системе, относительно которой стержень покоится.

Если стержень длины l ₀ = х ₂ — х ₁ покоится относительно системы К, то для определения его длины в системе. К ' нужно отметить координаты концов х ₂ и х ₁ в один и тот же момент времени t '₁ = t '₂ = b. Разность l = х '₂ — х '₁ даст длину стержня в системе К ', относительно которой он движется со скоростью v. Использовав первое из уравнений (37.10), снова придем к соотноше­нию (38.1).

Заметим, что в направлении осей у и z размеры стержня одинаковы во всех системах отсчета.

Итак, у движущихся тел размеры их в направлении движения сокращаются тем больше, чем больше скорость движения. Это явление называется лоренцовым (или фитцджеральдовым) сокращением. Любопытно, что визуально (или на фотографии) изменение формы тел, даже при сравнимых со скоростью света скоростях не может быть обнаружено. Причина этого весьма проста. Наблюдая визуально или фотографируя какое-либо тело, мы регистрируем импульсы света от разных участков тела, достигшие одновременно сетчатки глаза или фотопластинки. Испускаются же эти импульсы не одновременно. Импульсы от более удаленных участков были испущены раньше, чем от более близких участков. Таким образом, если тело движется, на сетчатке глаза или на фотографии получается искаженное изображение тела. Соответствующий расчет показывает, что следствием указанного искажения будет уничтожение лоренцева сокращения, так что тела кажутся не искаженными, а лишь повернутыми. Следовательно, тело сферической формы даже при больших скоростях движения будет восприниматься визуально как тело сферического очертания.

Длительность событий в разных системах. Пусть в точке, неподвижной относительно системы К', происхо­дит событие, длящееся время Δt₀ = t'₂ — t'₁. Началу события соответствует в этой системе координата х'₁ = а и момент времени t'₁, концу события — координата х'₂ = а и момент времени t'₂. Относительно системы К точка, в которой происходит событие, перемещается. Согласно формулам (37.10) началу и концу события соответствуют в системе К:

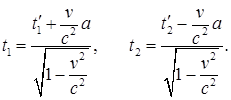
Откуда

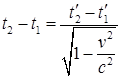
Введя обозначение t₂ — t₁ = Δt, получим:

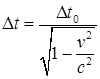(38.2)

') Если бы лоренцева сокращения не было, быстро движущиеся тела должны были бы представляться вытянутыми в направлении движения.

Дата добавления: 2014-01-04