
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Необхідна і достатня умови, пряма і обернена теореми
|
|
|
|
Поняття множини. Логічна символіка.
Розділ 4. Вступ до математичного аналізу
Поняття множини є одним з основних понять математики і не може бути визначене через більш прості поняття. Можна сказати, що множина є сукупність певних елементів (предметів, об’єктів), об’єднаних якоюсь спільною властивістю; сукупність, яка мислиться як одне ціле. Можна, наприклад, розглядати множину навчальних тижнів даного навчального року, множину студентів даного факультету, множину молекул в даному об’ємі речовини, тощо. В математиці здебільшого розглядаються множини чисел, точок, фігур, функцій і т.д. Конкретна множина вважається визначеною, якщо є можливість для всякого елемента дати цілком однозначну відповідь – належить даний елемент до множини, чи не належить.
Множини позначають звичайно великими літерами латинського алфавіту: 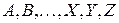 , а їх елементи – малими літерами. Якщо а є елементом множини А, то пишуть
, а їх елементи – малими літерами. Якщо а є елементом множини А, то пишуть 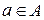 ; в противному разі
; в противному разі 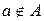 . Множина, яка не має елементів, називається порожньою і позначається
. Множина, яка не має елементів, називається порожньою і позначається 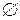 . Множини А і В називаються рівними, якщо вони складаються з одних і тих самих елементів. Отже, рівність
. Множини А і В називаються рівними, якщо вони складаються з одних і тих самих елементів. Отже, рівність 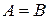 означає, що одна і та ж множина позначена різними літерами. Запис
означає, що одна і та ж множина позначена різними літерами. Запис  , або
, або 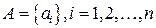 означає, що множина А складається з елементів
означає, що множина А складається з елементів 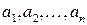 .
.
Математичні міркування, формулювання теорем і означень часто можуть бути записані більш стисло і зручно для запам’ятовування, якщо користуватись символікою, прийнятою в логіці. Розглянемо деякі поняття і позначення математичної логіки.
Висловленням або твердженням будемо називати оповідне речення, відносно якого можна встановити, істинне воно чи хибне. Позначати твердження будемо малими грецькими літерами 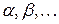 . Наприклад
. Наприклад 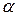 : „9 ділиться на 4”,
: „9 ділиться на 4”,  : „Одеса – обласний центр”,
: „Одеса – обласний центр”, 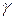 : „діагоналі ромба взаємно перпендикулярні”. Тут твердження
: „діагоналі ромба взаємно перпендикулярні”. Тут твердження 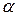 хибне,
хибне,  і
і 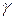 – істинні.
– істинні.
В математичних текстах часто зустрічаються вирази „для всякого (кожного, будь-якого)” і „існує”. Для цих виразів прийнято відповідно позначення 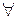 (від англійського „Any”) і
(від англійського „Any”) і 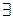 (від англійського „Exist”).
(від англійського „Exist”).
Запис 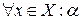 означає „для всякого елемента х множини Х істинним є твердження
означає „для всякого елемента х множини Х істинним є твердження 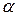 ” (символ
” (символ 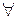 називають квантором загальності).
називають квантором загальності).
Запис 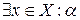 означає „існує елемент х множини Х, для якого істинним є твердження
означає „існує елемент х множини Х, для якого істинним є твердження 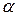 ” (символ
” (символ 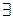 називають квантором існування).
називають квантором існування).
Приклад. Запишемо, використовуючи логічну символіку, твердження „функція 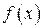 обмежена на множині А ”. Це означає: існує таке число
обмежена на множині А ”. Це означає: існує таке число 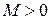 , що для будь-якого
, що для будь-якого 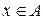 має місце нерівність
має місце нерівність 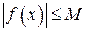 , або, в логічних символах:
, або, в логічних символах:
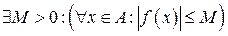 .
.
Формулювання будь-якої теореми має вигляд: „якщо істинне 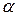 , то істинне
, то істинне  ”, або, що теж саме, „з
”, або, що теж саме, „з 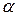 випливає
випливає  ”. Це записується
”. Це записується 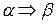 (знак
(знак 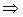 – символ імплікації).
– символ імплікації).
В цьому разі кажуть, що 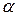 – умова,
– умова,  – висновок теореми, або (якщо теорема вірна), що умова
– висновок теореми, або (якщо теорема вірна), що умова 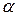 достатня для
достатня для  , а умова
, а умова  необхідна для
необхідна для 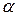 .
.
Теорема 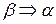 називається оберненою по відношенню до теореми
називається оберненою по відношенню до теореми 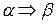 , яка зветься прямою. Очевидно, в свою чергу теоремою, оберненою до
, яка зветься прямою. Очевидно, в свою чергу теоремою, оберненою до 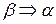 є
є 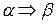 , тому ці дві теореми називаються взаємно оберненими. Якщо пряма теорема є вірною, то обернена може бути як вірною, так і не вірною.
, тому ці дві теореми називаються взаємно оберненими. Якщо пряма теорема є вірною, то обернена може бути як вірною, так і не вірною.
Приклади.
1. Пряма теорема. Якщо три вектори компланарні, то їх змішаний добуток дорівнює нулю.
Обернена теорема. Якщо змішаний добуток трьох векторів дорівнює нулю, то ці вектори компланарні.
В даному разі вірними є і пряма і обернена теорема.
2. Пряма теорема. Якщо визначник містить нульовий рядок, то він дорівнює нулю.
Обернена теорема. Якщо визначник дорівнює нулю, то він містить нульовий рядок.
Тут теорема пряма є вірною, а обернена – невірною.
Нехай вірною є теорема „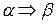 ”. Тоді, як сказано вище, умова
”. Тоді, як сказано вище, умова 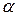 достатня для
достатня для  , а умова
, а умова  необхідна для
необхідна для 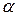 . Якщо при цьому вірною є і обернена теорема „
. Якщо при цьому вірною є і обернена теорема „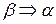 ”, то в свою чергу умова
”, то в свою чергу умова  достатня для
достатня для 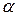 , а умова
, а умова 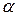 необхідна для
необхідна для  . Таким чином в даному разі умова
. Таким чином в даному разі умова 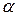 є необхідною і достатньою для
є необхідною і достатньою для  (а
(а  – необхідною і достатньою для
– необхідною і достатньою для 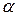 ). В цьому випадку твердження
). В цьому випадку твердження 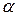 і
і  еквівалентні (рівносильні):
еквівалентні (рівносильні): 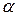 істинне тоді і тільки тоді, коли істинне
істинне тоді і тільки тоді, коли істинне  . Це позначається
. Це позначається 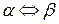 (знак
(знак 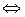 – символ еквівалентності). Так, у розглянутому вище прикладі 1 пряма і обернена теореми можуть бути об’єднанні одним формулюванням: „Для того, щоб три вектори були компланарні, необхідно і достатньо, щоб їх змішаний добуток дорівнював нулю”, або „Три вектори компланарні тоді і тільки тоді, якщо їх змішаний добуток дорівнює нулю”.
– символ еквівалентності). Так, у розглянутому вище прикладі 1 пряма і обернена теореми можуть бути об’єднанні одним формулюванням: „Для того, щоб три вектори були компланарні, необхідно і достатньо, щоб їх змішаний добуток дорівнював нулю”, або „Три вектори компланарні тоді і тільки тоді, якщо їх змішаний добуток дорівнює нулю”.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1152; Нарушение авторских прав?; Мы поможем в написании вашей работы!