Пряма в просторі. Способи завдання прямої

Як ми бачили в п. 3.2, лінію в просторі можна визначити як лінію перетину двох поверхонь. Зокрема, пряму лінію (l) можна задати як лінію перетину двох площин:

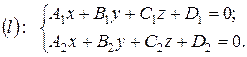(3.19)

Рівняння (3.19) називають загальними рівняннями прямої. Для того, щоб рівняння (3.19) визначали пряму, площини повинні бути не паралельними, тобто коефіцієнти при x, y, z у рівняннях (3.19) повинні бути не пропорційними.

Пряма може бути також задана якою-небудь її точкою і вектором , колінеарним цій прямій.

Означення. Ненульовий вектор = =(m, n, q) називається напрямним вектором прямої (l), якщо він колінеарний до цієї прямої (║(l)) (рис. 3.9).

Довільна точка простору належить до даної прямої (l) тоді і тільки тоді, коли вектор 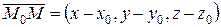колінеарний вектору , а умовою колінеарності векторів є пропорційність відповідних координат (п.2.4, формула (2.6)):

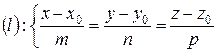. (3.20)

Рівняння (3.20) називають канонічними рівняннями прямої.

Якщо в рівняннях (3.20) позначити через t коефіцієнт пропорційності, то рівняння (3.20) будуть еквівалентні трьом рівнянням:

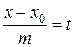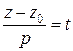, , , або

(3.21)

Рівняння (3.21) називають параметричними рівняннями прямої. Якщо параметр t інтерпретувати як час, то рівняння (3.21) являють собою рівняння рівномірного і прямолінійного руху точки. Вектор є сталий вектор швидкості точки, а пряма (l) – її траєкторія.

Як відомо, пряма однозначно визначається двома своїми точками. Якщо пряма (l) проходить через дві задані точки і , то вектор є напрямним вектором 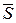цієї прямої. Тоді рівняння (3.20) матимуть вигляд:

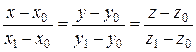. (3.22)

Вони називаються рівняннями прямої за двома точками.

В деяких задачах виникає потреба переходу від загальних рівнянь прямої (3.19) до канонічних рівнянь (3.20).

Якщо задано загальні рівняння прямої (3.19):

то для переходу до канонічних рівнянь потрібно:

а) визначити координати напрямного вектора 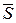прямої;

б) визначити координати однієї з точок прямої М ₀.

Напрямний вектор 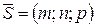прямої, як лінії перетину двох площин, ортогональний до нормальних векторів цих площин і , отже колінеарний їх векторному добутку: 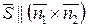. Можна, наприклад, взяти просто 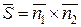. Обчисливши 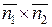, знайдемо координати напрямного вектора .

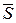Щоб визначити координати однієї з точок прямої, розглянемо рівняння прямої (3.19) як систему двох рівнянь з трьома невідомими x, y і z. Отже третя невідома є вільною (див. п. 1.5). Надаючи вільній невідомій довільного фіксованого значення z ₀, розв’яжемо систему (3.19) відносно решти невідомих. Одержаний розв’язок і дає координати точки , яка лежить на даній прямій.

Після цього залишається підставити координати напрямного вектора 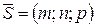і координати точки в рівняння (3.20).

Приклад 1. Пряму задано рівняннями

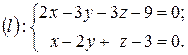
Написати її канонічні рівняння.

Розв’язання. а) Знаходимо напрямний вектор :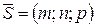

, ,

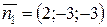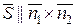, можемо взяти .

б) Знаходимо координати точки .

Нехай z ₀ = 0, тоді рівняння прямої приймають вигляд

Розв’язавши цю систему, одержуємо , .

Отже, точка належить до даної прямої. Підставляючи знайдені координати напрямного вектора 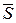і точки в в рівняння (3.20), маємо канонічні рівняння заданої прямої

.

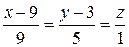Приклад 2. Написати канонічні рівняння прямої, яка проходить через точки М ₀(1;–1;3) і М ₁(4;1;–1).

Розв’язання. Рівняння прямої, що проходить через дві задані точки, записуються згідно з формулою (3.22). Підставляючи в цю формулу координати точок М ₀ і М ₁, одержимо

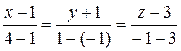, або

.

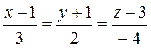Це і є канонічні рівняння заданої прямої.

Приклад 3. Написати параметричні рівняння прямої, яка проходить через точки М ₀(1;–1;3) і М ₁(1;1;–1).

Розв’язання. Знайдемо напрямний вектор цієї прямої 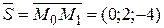, і тоді ми можемо написати параметричні рівняння прямої за формулами (3.21):

Приклад 4. Написати канонічні рівняння прямої (l), яка проходить через точку М ₀(2;0;1) і паралельна прямій

Розв’язання. В умові задачі вказано координати точки М ₀, через яку проходить шукана пряма (l). Щоб написати її канонічні рівняння, потрібно знати координати напрямного вектора 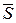цієї прямої. Згідно з умовою , отже і напрямні вектори цих прямих колінеарні: 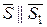. В цьому пункті показано, що , де і 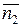– нормальні вектори площин, лінією перетину яких є пряма (l ₁). Значить і 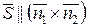. Обчислюємо за формулою (2.23) з п.2.7:

.

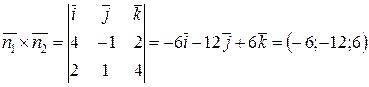Для спрощення можемо взяти . Тоді канонічні рівняння шуканої прямої (l) матимуть вигляд

.

Приклад 5. Написати рівняння прямої (l), яка проходить через точку 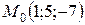перпендикулярно до площини .

Розв’язання. За напрямний вектор прямої (l) можна взяти нормальний вектор площини (Р):

.

Тоді канонічні рівняння шуканої прямої є:

.

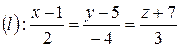Дата добавления: 2014-01-04