
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторний добуток векторів
|
|
|
|
Означення. Векторним добутком вектора  на вектор
на вектор  називається вектор
називається вектор 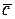 , який визначається такими трьома умовами:
, який визначається такими трьома умовами:
а) 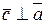 і
і 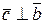 ;
;
б) вектори  ,
,  і
і 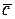 утворюють праву трійку векторів (див. п. 2.3);
утворюють праву трійку векторів (див. п. 2.3);
в) довжина вектора 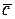 обчислюється за формулою
обчислюється за формулою
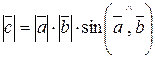 .
.
Векторний добуток вектора  на вектор
на вектор  позначається
позначається 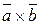 або
або 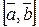 .
.
Геометричний зміст векторного добутку. Довжина векторного добутку дорівнює площі паралелограма, побудованого на векторах  і
і  ,
,
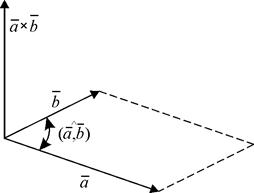 |
віднесених до спільного початку (рис. 2.11).
Рис. 2. 11
Перелічимо основні властивості векторного добутку.
1) Векторний добуток дорівнює нуль-вектору тоді і тільки тоді, коли співмножники колінеарні: 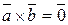 рівносильне
рівносильне  ||
|| , тому що в цьому випадку
, тому що в цьому випадку 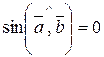 . Зокрема
. Зокрема  .
.
2) Векторний добуток антикомутативний:
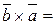
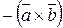 .
.
Справді, при зміні порядку співмножників паралелограм не зміниться, отже 
 , але напрям
, але напрям  протилежний напряму
протилежний напряму 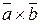 , бо як вектори
, бо як вектори  ,
,  ,
, 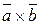 так і вектори
так і вектори  ,
,  ,
,  утворюють праві трійки. Це означає, що дивлячись з кінця вектора
утворюють праві трійки. Це означає, що дивлячись з кінця вектора 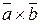 , ми бачимо найкоротший поворот від
, ми бачимо найкоротший поворот від  до
до  проти годинникової стрілки, а дивлячись з кінця вектора
проти годинникової стрілки, а дивлячись з кінця вектора 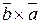 , бачимо проти годинникової стрілки найкоротший поворот від
, бачимо проти годинникової стрілки найкоротший поворот від  до
до  .
.
3) Асоціативність відносно скалярного множника:
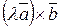 =
= 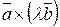 =
=  .
.
Дійсно, наприклад, 
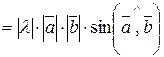 і
і 
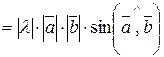 , крім того
, крім того 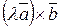 і
і  колінеарні, бо кожен з них перпендикулярний до вектора
колінеарні, бо кожен з них перпендикулярний до вектора  і до вектора
і до вектора  . Напрям у них однаковий, що при
. Напрям у них однаковий, що при  є очевидним; при
є очевидним; при  вектори
вектори  і
і  мають протилежні напрями, тому вектор
мають протилежні напрями, тому вектор 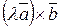 напрямлений протилежно вектору
напрямлений протилежно вектору 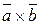 , але при цьому вектор
, але при цьому вектор  також напрямлений протилежно вектору
також напрямлений протилежно вектору 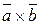 , значить і при
, значить і при  буде
буде 
 , тому і в цьому разі
, тому і в цьому разі 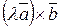 =
=  .
.
4) Дистрибутивність відносно додавання:
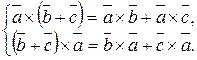
Обґрунтування цієї властивості розглянемо пізніше (за допомогою формули (2.23)).
Зауваження. Сформульовані властивості дозволяють при векторному множенні векторних многочленів виконувати дії почленно (розкривати дужки) і об’єднувати числові коефіцієнти векторних співмножників. Але слід пам’ятати, що порядок співмножників векторного добутку є істотним, і при перестановці співмножників знак векторного добутку змінюється на протилежний.
Приклад. 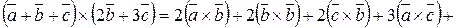
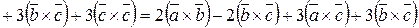 =
=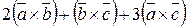 .
.
 Тут враховано, що
Тут враховано, що 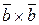 =
= =
= .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 927; Нарушение авторских прав?; Мы поможем в написании вашей работы!