Вихрове електричне поле

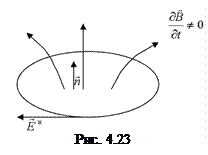Розглянемо замкнений провідний контур, що перебуває в змінному магнітному полі (рис 4.23). Згідно з законом Фарадея (див. §4.8), в цьому контурі індукується електрорушійна сила

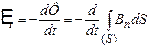(4.53)

і, як наслідок, виникає індукційний струм; тобто на вільні заряди контура діють сторонні сили. Оскільки контур нерухомий, то ці сили не можна ототожнити з силою Лоренца. Для відповіді на питання про природу сторонніх сил в розглянутому випадку Максвелл висунув гіпотезу про те, що змінне магнітне поле породжує в навколишньому просторі (навіть без провідного контура) вихрове електричне поле, яке і викликає появу індукційного струму. Напруженість цього поля позначають 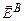, на відміну від напруженості електростатичного поля (створеного електричними зарядами), яку будемо надалі позначати Тоді за означенням електрорушійної сили:

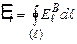. (4.54)

З (4.53) і (4.54) одержимо

.

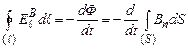Оскільки контур нерухомий, то в останньому рівнянні можна поміняти місцями операції інтегрування та диференціювання. І врахувавши, що в загальному , запишемо

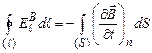(4.55)

На відміну від електростатичного, поле 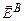, породжене змінним магнітним полем, є вихровим, бо його циркуляція відмінна від нуля 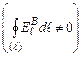, і тому силові лінії цього поля замкнені.

Якщо ж у просторі одночасно існують і вихрове (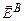), і електростатичне() поля, то за принципом суперпозиції напруженість результуючого поля

.

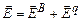Як було показано в розділі 3, ч.1, циркуляція напруженості електростатичного поля 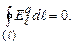Тому рівняння (4.55) можна узагальнити:

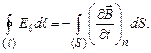(4.56)

Ми отримали перше рівняння Максвелла: циркуляція вектора напруженості електричного поля дорівнює взятій з протилежним знаком швидкості зміни магнітного потоку через довільну поверхню, що опирається на контур циркуляції (рис. 4.23).

§4.12. Струми зміщення. Теорема про циркуляцію вектора напруженості магнітного поля (закон повного струму)

У відповідності із законом Біо-Савара-Лапласа (див. §4.2), електричний струм завжди породжує магнітне поле. Але струм – це напрямлений рух електричних зарядів. Навколо ж заряду, як нерухомого, так і рухомого, існує електричне поле. Можна сказати, що змінне в просторі електричне поле породжує магнітне поле, і закон Біо-Савара-Лапласа є математичним відображенням цього факту. Максвелл же висунув гіпотезу про те, що не тільки змінне в просторі, а і змінне в часі електричне поле породжує магнітне поле. На практиці змінне в часі електричне поле отримаємо, наприклад, в процесі розрядки конденсатора. Якщо обкладки конденсатора, зарядженого з поверхневою густиною заряду , сполучити провідником (рис. 4.24), то по провіднику потече електричний струм (струм провідності) 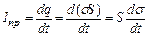, де S – площа пластини конденсатора. Густина струму провідності

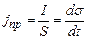. (4.57)

Але між обкладками конденсатора впорядкований рух зарядів припиняється. Виникає питання: чи зникає там і магнітне поле, яке завжди пов’язане зі струмом? Гіпотеза Максвелла (пізніше підтверджена експериментально) полягає у тому, що магнітне поле існує і між обкладками конденсатора, оскільки там існує змінне в часі електричне поле. Силовою характеристикою електричного поля в конденсаторі є вектор електричного зміщення 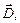модуль якого, як показано в розділі 3 ч.1, дорівнює поверхневій густині вільних зарядів на обкладках конденсатора: 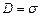. Оскільки в процесі розрядки конденсатора поверхнева густина заряду зменшується, існує відмінна від нуля похідна

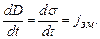(4.58)

Цю похідну Максвелл і назвав густиною струму зміщення; цей струм не пов'язаний з рухом зарядів в просторі між обкладками конденсатора, він існує незалежно від того, чи є в конденсаторі діелектрик, чи там вакуум. Потрібно лише, щоб існувало змінне електричне поле, яке викликає струм зміщення і породжене ним магнітне поле. З (4.57) і (4.58) видно, що 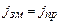, тобто струм провідності в провіднику неперервно переходить в струм зміщення в діелектрику (або у вакуумі) (рис. 4.24).

Максвелл ввів також поняття повного струму, як суму струмів провідності та зміщення,

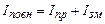. (4.59)

В розімкненому електричному колі лінії повного струму завжди замкнені: в провідниках вони пов’язані з напрямленим рухом електричних зарядів, а в діелектриках (або вакуумі) – зі змінним електричним полем.

В §4.3 була встановлена теорема про циркуляцію вектора напруженості магнітного поля струму провідності:

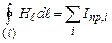. (4.60)

По теорії Максвелла, в правій частині (4.60) повинна стояти сила повного струму. Отже, після підстановки (4.59) в (4.60) одержимо 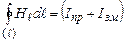. Або, якщо виразити силу струму через його густину, а також врахувати (4.58), останній вираз можна записати у вигляді

. (4.61)

Рівняння (4.61) носить назву закону повного струму або 3-го рівняння Максвелла: циркуляція вектора напруженості магнітного поля дорівнює алгебраїчній сумі сил струмів провідності та струмів зміщення через поверхню S, обмежену контуром циркуляції.

Дата добавления: 2014-01-04