Додавання однаково направлених гармонічних коливань однакової частоти

Часто матеріальна точка бере участь у двох і більше коливаннях. Наприклад, підвішена до стелі вагона на пружині кулька здійснює коливання відносно точки підвісу, яка у свою чергу коливається на ресорах вагона; таким чином, кулька буде здійснювати рух, який складається із двох коливань одного напрямку.

Нехай матеріальна точка бере участь у двох однаково направлених гармонічних коливаннях однакової частоти, але з різними амплітудами і початковими фазами:

,

.

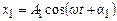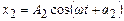Очевидно, результуюче коливання є також гармонічним і буде описуватись виразом

.

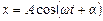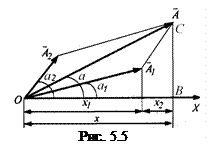
Одержати цей вираз можна аналітично, але легше скласти коливання векторним способом. Для цього у момент часу 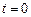побудуємо векторну діаграму додавання цих коливань (рис. 5.5), відклавши амплітуди як вектори під кутом 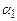та до осі x.

Оскільки вектори амплітуд обертаються з однаковою кутовою швидкістю, рівною циклічній частоті ω, то кут між векторами 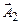і 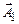залишається рівним 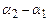. Тоді результуючий вектор

.

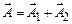З рис. 5.5 за теоремою косинусів маємо

або

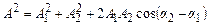. (5.18)

З рис. 5.5 видно, що початкову фазу результуючого коливання можна визначити за співвідношенням

.

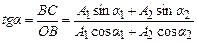Із (5.18) випливає, що А залежить від різниці початкових фаз 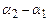, тому

.

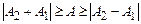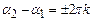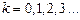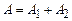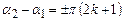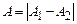Зокрема, коли , де , то ; коливання, що додаються, здійснюються «у фазі». Коли ж , то ; коливання здійснюються «у протифазі».

Якщо 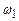і 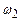близькі, то результуюча частота 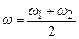, і амплітуда результуючого коливання повільно і періодично змінюється. Це явище називається биттям.

Дата добавления: 2014-01-04