
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило фаз Гиббса
|
|
|
|
Гетерогенное равновесие многокомпонентных систем без химических реакций
Если гомогенная однокомпонентная система находится в равновесии, то ее состояние определяется значениями двух независимых переменных (параметров), так как величина третьей переменной определяется по уравнению состояния
φ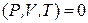 .
.
Если в однокомпонентной системе находятся в рановесии две фазы, то ее состояние уже определяется только одной независимой переменной, поскольку появляется еще одно уравнение связи (уравнение Клапейрона – Клаузиуса, связывающее температуру и давление)
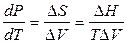 .
.
В точке пересечения кривых, построенных по уравнению Клапейрона – Клаузиуса для равновесия двух фаз с третьей (например, жидкость – пар и кристалл – пар), все три фазы находятся в равновесии. Эта точка жестко фиксирована и в ней нет ни одной независимой переменной. Точку равновесия трех фаз в однокомпонентной системе называют тройной точкой.
Определим число степеней свободы (υ) одно- и многокомпонентных гетерогенных систем как число независимых термодинамических параметров, определяющих состояние системы, изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз. Для однокомпонентной равновесной системы число степеней свободы в зависимости от числа фаз определяется исходя из уравнений связи, для многокомпонентных систем необходимо найти общее решение проблемы, а именно установить связь между числом компонентов в системе (K), числом равновесных фаз (Ф) и числом степеней свободы системы (υ).
Рассмотрим систему, содержащую К компонентов и состоящую из Ф фаз, находящихся в равновесии между собой. Состав каждой из фаз определяется концентрациями (К – 1) компонентов, а так как число всех фаз равно Ф, то состав всей системы определеляется Ф (К – 1) концентрациями всех компонентов. Для полного описания состояния системы необходимо учесть ещё и внешние параметры (температура и давление). Таким образом, общее число переменных равно Ф (К – 1) + 2.
Условием равновесия гетерогенной системы из Ф фаз и К компонентов является постоянство температуры и давления, а также равенство всех химических потенциалов каждого из компонентов во всех фазах. Следовательно,
по условию механического равновесия
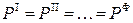 ;
;
по условию термического равновесия
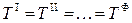 ;
;
по условию химического равновесия
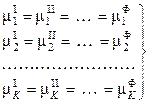 (10.1)
(10.1)
В равенствах (10.1) верхние индексы обозначают номера фаз, нижние индексы относятся к компонентам.
Каждое значение химического потенциала m i является функцией температуры, давления и концентрации всех компонентов. Например, для двухкомпонентной системы
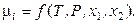
Следовательно, каждое равенство из (10.1), например,
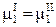 ,
,
представляет собой уравнение, связывающее переменные системы. Эти уравнения (уравнения связи) уменьшают число независимых переменных, характеризующих систему. Число этих уравнений равно К (Ф – 1).
Итак, число действительно независимых переменных (число степеней свободы) многокомпонентной системы равно
 , (10.2)
, (10.2)
откуда
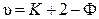 . (10.3)
. (10.3)
Последнее соотношение было получено Дж. Гиббсом и носит название правила фаз Гиббса: число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только давление и температура, равно числу компонентов системы плюс два, минус число фаз. Данному правилу подчиняются все равновесные системы, состоящие из любого числа фаз и любого числа веществ.
Перепишем уравнение (10.3) в виде
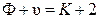 , (10.4)
, (10.4)
тогда при υ = 0 (минимальное число степеней свободы) находим, что
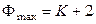 , (10.5)
, (10.5)
т. е. максимальное число фаз в гетерогенной системе при равновесии равно числу компонентов плюс два. Таким образом, в однокомпонентной системе максимально могут находиться в равновесии три фазы, в двухкомпонентной – четыре и т. д.
Следует отметить, что если значение одного из внешних параметров фиксируется (P = const или Т = const), то число степеней свободы системы уменьшается на единицу и правило фаз Гиббса записывается следующим образом:
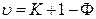 . (10.6)
. (10.6)
Далее, если в гетерогенной системе две фазы совпадают по составу, то для концентраций компонентов появляются дополнительные уравнения связи типа
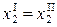 .
.
В общем случае число таких уравнений связи равно (К – 1) и число степеней свободы определяется выражением
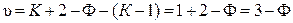 . (10.7)
. (10.7)
Итак, система, в которой две фазы совпадают по составу (например, азеотроп), будет вести себя как однокомпонентная независимо от числа компонентов.
Если в системе совпадают по составу три фазы, то
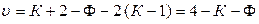 . (10.8)
. (10.8)
Для нульвариантной (инвариантной) системы υ = 0, поэтому
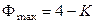 .
.
Если система однокомпонентная (К = 1), то Фmax = 3. Если система двухкомпонентная, то Фmax = 2, однако это противоречит условию поставленной задачи: Ф = 3. Поэтому три фазы, совпадающие по составу, могут существовать только в однокомпонентной системе (тройная точка).
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1724; Нарушение авторских прав?; Мы поможем в написании вашей работы!