Общие условия равновесия в закрытых системах

С помощью фундаментального уравнения термодинамики, записанного для различных процессов, и характеристических функций можно установить общие условия равновесия и устойчивости закрытых систем.

Рассмотрим сначала изолированную систему: U, V = const. Фундаментальное уравнение термодинамики

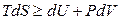
в случае изолированной системы преобразуется в

. (4.103)

Э нтропия изолированной системы при необратимых процессах увеличивается. Когда эти процессы прекратятся и наступит устойчивое равновесие, энтропия изолированной системы будет максимальна (и определяться условиями изоляции – значениями U и V).

О бщим условием устойчивого равновесия изолированной системы является максимум ее энтропии:

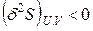; , (4.104)

то есть первая вариация энтропии равна нулю, а вторая вариация меньше нуля. Оператор δ означает бесконечно малое приращение стоящей справа от него функции S при любом мыслимом в изолированной системе процессе в отличие от оператора d, который относится к какому-либо одному определенному процессу.

В закрытой системе условия равновесия будут уже другими, зависящими от способа взаимодействия системы с окружающей средой. Рассмотрим основные случаи.

1). Простая (только работа расширения) система при S, V = const. На основании фундаментального уравнения термодинамики

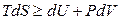или .

Из последнего неравенства следует, что при S, V = const

,

то есть самопроизвольные необратимые процессы будут протекать с уменьшением внутренней энергии. Так как самопроизвольные процессы заканчиваются в состоянии равновесия, то внутренняя энергия системы в этом состоянии будет минимальной. Условие равновесия для простой изохорно-изоэнтропийной системы:

; . (4.105)

2). Простая система при S, P = const. Используя функцию состояния Н – энтальпию, фундаментальное уравнение термодинамики запишетcя

.

Тогда при S, P = const

.

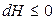В состоянии равновесия dH = 0. Таким образом, в необратимых процессах энтальпия изобарно-изоэнтропийной системы убывает, достигая минимума в состоянии равновесия:

; . (4.106)

3). Простая изохорно-изотермическая система (при Т, V = const). Фундаментальное уравнение термодинамики для такой системы удобно записать в виде

,

откуда с учетом dT = 0 и dV = 0 получаем

.

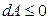В изохорно-изотермической системе энергия Гельмгольца в необратимых процессах убывает, достигая минимума в состоянии устойчивого равновесия:

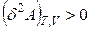; . (4.107)

4). Простая изобарно-изотермическая система (при T, P = const). В данном случае фундаментальное уравнение термодинамики лучше всего записать через энергию Гиббса

,

так как dT = 0 и dP = 0, то

.

В изобарно-изотермической системе энергия Гиббса в необратимых процессах убывает, достигая минимума в состоянии устойчивого равновесия:

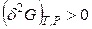; . (4.108)

Таким образом, общие условия устойчивого равновесия для простых систем в различных условиях определяются экстремумами характеристических функций: максимум энтропии (изолированная система) и минимум внутренней энергии, энтальпии, энергий Гиббса и Гельмгольца.

Характеристические функции системы при заданных значениях естественных переменных могут иметь несколько экстремумов. Состояния, соответствующие наибольшему (энтропия) или наименьшему (U, H, A, G) из них, называются стабильными (абсолютно устойчивые состояния), другие – метастабильными (полуустойчивыми) состояниями. Состояние системы называется лабильным, если его любые бесконечно малые изменения приводят к возрастанию энтропии (изолированная система) или уменьшению внутренней энергии, энтальпии, энергий Гиббса и Гельмгольца (закрытые системы). Лабильные состояния – это абсолютно неустойчивые и поэтому физически нереализуемые состояния. Критерий лабильных состояний записывается таким образом:

, .

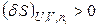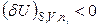Для химиков особый интерес представляют две группы равновесий – фазовые и химические равновесия. В первой группе – фазовые равновесия – равновесие в системе устанавливается (помимо прочих условий) за счет перераспределения масс компонентов между отдельными фазами. Во второй группе – химические равновесия – достижение равновесия связано в первую очередь с протеканием химических реакций. Рассмотрим сначала фазовые равновесия.

Дата добавления: 2014-01-04