Дефект маси та енергія зв’язку ядра. Ядерні сили

Користуючись таблицею мас ізотопів легко пересвідчитись, що маса ядра 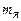завжди менша від суми мас нуклонів, з яких воно складається. Величину

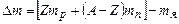(8.3)

називають дефектом маси ядра. Його існування зумовлене тим, що при об’єднанні нуклонів в ядро виділяється енергія. Її можна розрахувати за формулою Ейнштейна

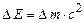, (8.4)

де с – швидкість світла у вакуумі. Очевидно, щоб розкласти ядро на невзаємодіючі нуклони, потрібно таку ж енергію затратити. Ця енергія

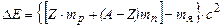(8.5)

називається енергією зв’язку ядра.

Для практичних застосувань співвідношення (8.5) зручно записувати у вигляді

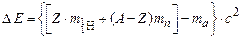, (8.6)

де 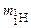– маса атома водню, а m_a – маса атома, ядро якого розглядається. При переході до наближеної формули (8.6) нехтують малою енергією зв’язку електронів; зручність цієї формули полягає у тому, що в довідниках наводяться не маси ядер 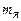, а маси атомів 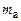. На основі (8.4) можна пересвідчитись, що 1а.о.м. еквівалентна енергії 931,5 МеВ; тому, виражаючи фігурну дужку формули (8.6) в а.о.м., для енергії зв’язку ядра в МеВ одержують

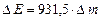. (8.7)

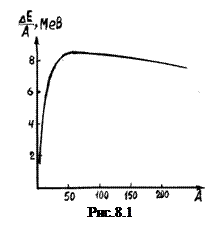
Очевидно, енергія зв’язку ядра характеризує міцність ядра. Зручно ввести в розгляд так звану питому енергію зв’язку 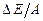(енергія зв’язку, що припадає на один нуклон). Розрахунки показують, що ця величина залежить від масового числа А елемента (рис.8.1).

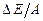Для легких ядер стрибкоподібно зростає до 6 – 7 МеВ, далі більш повільно зростає до максимального значення 8,7 МеВ для елементів з масовим числом А ~ 50 – 60, а тоді повільно зменшується для важких елементів (наприклад, для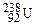 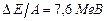). Аналіз кривої показує:

- найбільш стійкими є ядра середньої частини таблиці елементів Менделєєва;

- енергетично можливими є два процеси, які повинні супроводжуватися виділенням енергії, – процес поділу важких ядер і процес синтезу легких ядер.

Величезна питома енергія зв’язку ядра свідчить, що між нуклонами в ядрі діють особливі сили, які значно переважають електромагнітну та гравітаційну взаємодію нуклонів. Ядерна взаємодія між нуклонами одержала назву сильної взаємодії. Ядерні сили характеризуються такими особливостями:

- короткодіючі: в ядрі, (на відстанях r ~10^–15м) зумовлюють ефективне притягання між нуклонами; поза ядром (при r > 10^–14м) практично зникають; при r < 10^–15м стають силами відштовхування і це суттєво, щоб ядро не колапсувало;

- зарядовонезалежні, тобто мають неелектричну природу;

- залежать від взаємної орієнтації спінів нуклонів;

- мають спін-орбітальний характер (залежать від взаємної орієнтації спіна і орбітального момента нуклона);

- є нецентральними (не напрямлені вздовж прямої, що з’єднує центри нуклонів);

- мають властивість насичення, тобто діють лише між найближчими сусідами.

У 1934 р. І.Є. Тамм висунув гіпотезу, що сильна взаємодія повинна мати обмінну природу. По аналогії з електромагнітною взаємодією, яка квантовою електродинамікою описується як процес віртуального обміну електронів фотонами

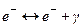, (8.8)

нуклони в ядрі повинні обмінюватись деякими віртуальними частинками з масою, відмінною від нуля. Дійсно, віртуальними називаються частинки, час життя яких менший від того, що визначається співвідношенням невизначеностей

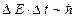, (8.9)

де 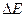– невизначеність енергії квантового стану, 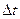– тривалість існування цього стану. Очевидно, радіус дії обмінних сил оцінюється величиною

,

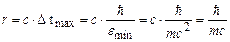тобто він може бути скінченним, якщо маса віртуальної частинки відмінна від нуля.

У 1935 р. Х. Юкава показав, що для пояснення величини ядерних сил слід припустити існування віртуальних частинок з масою у 200–300 разів більшою від маси електрона. Віртуальна частинка може стати реальною, якщо їй надати достатньої енергії. Подібні частинки з масою 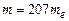у 1936 р. виявили К. Андерсон і С. Неддермайер в космічних променях; вони дістали назву м’юонів (μ -мезонів). Проте, лабораторними дослідженнями було доведено, що м’юони практично не взаємодіють з ядрами, тому не можуть бути носіями ядерних сил. У 1947 р. С. Поуелл і Дж. Оккіаліні виявили в космічних променях ще один тип мезонів, які назвали 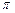-мезонами (піонами). Вони і виявились носіями ядерних сил. Існують три типи піонів: 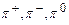. Заряд 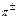–мезонів за абсолютною величиною рівний елементарному зарядові е, їх маси: 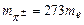, 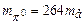. Спін усіх 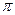– мезонів S = 0, всі вони нестабільні; час життя 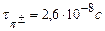, 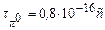. В основному піони розпадаються за схемами:

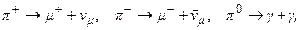
де 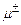– м’юони, 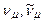– м’юонні нейтрино і антинейтрино, γ – g‑квант.

За рахунок процесів:

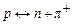, (8.10)

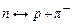, (8.11)

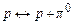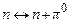, (8.12)

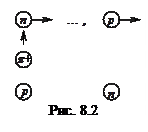здійснюється обмін нуклонів віртуальними піонами, що приводить до сильної взаємодії нуклонів. Така модель підтверджується дослідами по розсіянню нейтронів на протонах. При проходженні пучка нейтронів через водень у пучку з’являються протони, які мають енергію і напрямок руху нейтронів; відповідне число нерухомих нейтронів виявляється в мішені. Природно припустити, що нейтрон, пролітаючи поблизу протона, захоплює віртуальний p⁺ -мезон. В результаті нейтрон перетворюється в протон, а протон, який втратив свій заряд, перетворюється в нейтрон (рис. 8.2).

На основі процесів (8.10), (8.11) можна також пояснити магнітні моменти протона і нейтрона. Від’ємний магнітний момент нейтрона зумовлений орбітальним рухом p^––мезона у віртуальному стані нейтрона (8.11);. аномальний магнітний момент протона (більший від одного магнетона) зумовлений орбітальним рухом p ⁺–мезона у віртуальному стані протона (8.10).

Незважаючи на пояснення природи ядерних сил, послідовна кількісна теорія ядра донині не побудована, бо являє собою громіздку квантову задачу багатьох тіл, в якій закон дії ядерних сил невідомий. Це спонукає йти по шляху створення моделей ядра, які, за рахунок введення певних параметрів, що підбираються в узгодженні з дослідом, дозволяють простими засобами описувати деяку сукупність властивостей ядра. Найбільш вживаними з них є краплинна та оболонкова моделі ядра.

Краплинна модель ядра (К.Вейцзеккер, Я.І.Френкель, Н.Бор, 1935–1939р.), базуючись на властивості насичення ядерних сил і молекулярних сил в рідині, уподібнює ядро до зарядженої краплини рідини. Це дозволило одержати напівемпіричну формулу для енергії зв’язку ядра і, зокрема, пояснити процеси поділу важких ядер.

Оболонкова модель ядра (М. Гепперт-Майєр, Х. Ієнсен, 1949–1950р.) базується на уявленні, що нуклони рухаються незалежно в усередненому центрально-симетричному полі. У зв’язку з цим виникають дискретні енергетичні рівні, які заповнюються нуклонами на основі принципу Паулі. Ці рівні групуються в оболонки, в кожній з яких може перебувати певне число нуклонів. Повністю заповнена оболонка є особливо стійким утворенням. Такими особливо стійкими (магічними) виявляються ядра, у яких число протонів Z або число нейтронів N рівні: 2, 8, 20, 28, 50, 82, 126. Ядра, у яких магічними є Z та N, називаються двічі магічними. 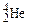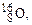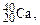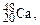Їх відомо п’ять: , 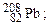вони особливо стійкі.

Відома також узагальнена модель ядра (О. Бор, Б. Моттельсон, 1952 – 1953 рр.), що є спробою синтезу двох попередніх. Проте, кожна з цих моделей не характеризує загальної поведінки ядер.

Дата добавления: 2014-01-04