Тема 2.3 Дизъюнктивная нормальная форма

Самостоятельная работа №2.

Отрицание относящиеся к переменной называется тесным (простым). Отрицание, не являющееся тесным, называется сложным.

Высказывательная форма называется приведенной, если она не содержит операции импликации и сложного отрицания.

Теорема: Для любой высказывательной формы существуют равносильные приведенные формы.

Доказательство:

1) Пусть высказывательная форма Ы – есть переменная (тривиально);

2) Пусть Ы - = ^┐ L и для L теорема 1 выполняется, т.е. существует L*, которое является приведенной формой: L*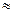L, тогда рассмотрим ^┐ L* применяя нужное число раз законы Моргана, получим, что внешнее отрицание перенесется внутрь либо на отрицание переменной, либо на отрицание отрицания переменной, таким образом ^┐ L – является приведенной высказывательной формой.

3) Пусть 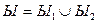, причем для теорема 1 выполняется, т.е. для них существуют равносильные приведенные высказывательные формы, т.к. они не содержат операции импликации и сложного отрицания.

4) Пусть , аналогично п.3

5) Пусть 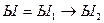, для теорема 1 выполняется, применяем закон импликации: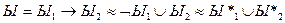

Символическая степень высказывания – это , причем 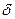может быть истиной, либо ложной, причем: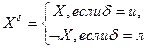

Свойства символической степени высказывания:

1.

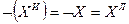
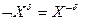
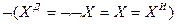
2.

Высказывательная форма, состоящая из переменных или отрицания переменных применением только одной операции дизъюнкции, называется элементарной дизъюнкцией.

Высказывательная форма, состоящая из элементарных конъюнкций, применением только одной операции дизъюнкции называется дизъюнктивной нормальной формой (ДНФ).

Совершенной дизъюнктивной формой формулы алгебры высказываний (СДНФ) называется ДНФ, в которой:

1. различны все члены дизъюнкции;

2. различны все члены каждой конъюнкции;

3. ни одна конъюнкция не содержит одновременно переменную и отрицание этой переменной;

4. каждая конъюнкция содержит все переменные, входящие в формулу, т.е. имеет вид

,

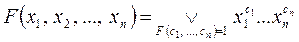где дизъюнкция берется по всем наборам с=(с₁, с₂, …, с_n) из 0 и 1, для которых F(c)=1.

Теорема (о СДНФ). Для всякой не равной тождественному нулю формулы логики высказываний F(x₁, x₂, …, x_n) существует такая формула F₁, зависящая от того же списка переменных и находящаяся в СДНФ относительно этого списка, что F₁ выражает собой формулу F. Формула F₁ определена однозначно с точностью до перестановки дизъюнктивных членов.

Опишем два способа приведения к совершенным нормальным формам.

1-й способ – аналитический.

Приведение к СДНФ. Алгоритм приведения.

1. привести формулу с помощью равносильных преобразований к ДНФ.

2. удалить члены дизъюнкции, содержащие переменную вместе с ее отрицанием (если такие окажутся);

3. из одинаковых членов дизъюнкции (если такие окажутся) удалить все, кроме одного;

4. из одинаковых членов каждой конъюнкции (если такие окажутся) удалить все, кроме одного;

5. если в какой-нибудь конъюнкции не содержится переменной x_i из числа переменных, входящих в исходную формулу, добавить к этой конъюнкции член 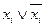и применить закон дистрибутивности конъюнкции относительно дизъюнкции;

6. если в полученной дизъюнкции окажутся одинаковые члены, воспользоваться предписанием из п. 3.

Полученная формула и является СДНФ данной формулы.

Привести следующие формулы к СДНФ с помощью равносильных преобразований:

1. ;

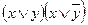2. ;

3. .

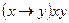Решение.

1. .

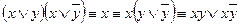2.

3.

2-й способ – табличный.

Составляем таблицу истинности для данной функции.

Строим таблицу значений формулы. Рассматриваем только те строки, в которых значение формулы равно единице. Каждой такой строке соответствует конъюнкция всех аргументов (без повторений). Причем, аргумент, принимающий значение 0, входит в нее с отрицанием, значение 1 – без отрицания. Наконец, образуем дизъюнкцию всех полученных конъюнкций.

Построить СДНФ для данных формул логики высказываний.

1. .

2.

Решение.

1. .

Строим таблицу истинности для формулы F:

№	x	y	z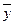

Рассматриваем только 4, 5 и 7 наборы, так как только на этих наборах формула принимает значение равное единице.

СДНФ имеет вид:

2.

Строим таблицу истинности для формулы F:

№	x	y	x® y	F=(x® y)ÙxÙy

СДНФ (1): № 3:

F = x y

Дата добавления: 2014-01-04