Тема 7.7 Деревья. Код Пруфера

Деревом называется всякий несвязный граф без циклов.

Граф, состоящий из изолированной вершины, тоже считается деревом.

Вершина дерева, степень которой равна 1, называется висячей.

Лесом называется граф представленный в виде объединения деревьев.

Теорема: Если у дерева n вершин, то ребер n-1.

Рассмотрим произвольное дерево с 11 вершинами, пронумерованными в произвольном порядке.

В результате возникает вопрос: сколько существует таких деревьев с 11 вершинами?

Английский математик Кэли нашел ответ на этот вопрос: деревьев с n вершинами можно создать столько, сколько существует последовательностей вида: 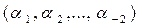, где и таких последовательностей будет n^n-2.

Немецкий математик Пруффер продолжил решать эту проблему и указал алгоритм, согласно которому любому дереву можно поставить во взаимно-однозначное соответствие – код.

Алгоритм:

1. выбираем висячую вершину с наименьшим номером.

2. удаляем ее вместе с принадлежащим ей ребром.

3. записываем номер вершины полученного дерева ближайшей к удаленной.

4. повторяем данные действия до тех пор пока не останется две висячие вершины, связанные между собой ребром.

1. вершина № 2

2. записываем вершину № 1

3. выбираем вершину № 3

4. записываем вершину № 1

и т.д., в результате получаем код: (1, 1, 5, 5, 6, 6, 6, 6, 5)

И наоборот, зная код можно изобразить дерево.

Алгоритм составления дерева по коду:

1. находим наименьшее натуральное число, которое не встречается в последовательности.

2. это число – номер вершины, которую необходимо соединить с вершиной, которая встречается первой в коде.

3. находим следующее число

Дан код (1, 5, 5, 3, 6, 4).

Количество вершин = 8,

1. наименьшее число, не встречающееся в последовательности – 2

2. строим эту вершину и соединяем ребром с вершиной №1

3. аналогично перебираем все цифры не встречающиеся в последовательности до 8.

Дата добавления: 2014-01-04