
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства матриц смежности и инцидентности
|
|
|
|
Задание графов матрицами
Пример.
Замечание.
1) Далее всюду при подсчете числа вхождений вершин в замкнутый маршрут (путь) начальную и конечную вершины будем считать за одно вхождение этой вершины в маршрут (путь).
2) При замкнутом маршруте (пути) e 1 e 2… ek обычно считается, что последовательности e 1 e 2… ek, e 2… eke 1, …, eke 1 e 2… ek –1 – различные записи одного и того же маршрута (пути).
Незамкнутый маршрут (путь), в котором все ребра (дуги) попарно различны, называется цепью. Цепь, в которой все вершины попарно различны, называется простой цепью. Замкнутый маршрут (путь), в котором все ребра (дуги) попарно различны, называется циклом (контуром). Цикл (контур), в котором все вершины попарно различны, называется простым.
Каковы минимальная длина простого цикла (контура) в (ориентированных) псевдографах, мультиграфах, графах?
Пусть p 1= v 1 e 1 v 2 e 2 v 3… ek –1 vk, p 2= vkekvk +1… em –1 vm – пути в орграфе G, где k ³2, m ³ k +1. назовем путь
p 1° p 2= v 1 e 1 v 2 e 2 v 3… ek –1 vkekvk +1… em –1 vm
композицией путей p 1 и p 2. Аналогично определяется композиция маршрутов.
Основными матрицами, описывающими граф, являются матрица смежности и матрица инцидентности.
Пусть дан граф G =(V, E), | V |= n, | E |= m.
Определение. Матрицей смежности графа G называется квадратная матрица AG размера n × n, в которой

Как по матрице смежности отличить орграф от неорграфа?
Замечание. Если G – мультиграф, то значение aij можно положить равным k, где k – кратность дуги (vi, vj).
Определение. Матрицей инцидентности неорграфа G называется матрица BG размера n × m, в которой

Определение. Матрицей инцидентности орграфа G называется матрица BG размера n × m, в которой

Пример. Построить граф с матрицей:
а)  ; б)
; б)  ; в)
; в) 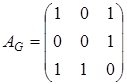 ;
;
г)  ; д)
; д) ; е)
; е)  .
.
С помощью введенных матриц удобно задавать графы для обработки на ЭВМ. Однако при большом количестве вершин матрицы могут оказаться слишком громоздкими. Другим способом представить граф в памяти машины является структура смежности: для каждой вершины графа составляется перечень ее последователей.
1) Сумма элементов матрицы AG, где G =(V, E) – мультиграф, V ={ v 1, v 2, …, vn }, по i -ой строке (или по i -ому столбцу) равна deg vi.
2) Суммы элементов матрицы AG, где G =(V, E) – ориентированный псевдограф, V ={ v 1, v 2, …, vn }, по i -ой строке и по i -ому столбцу соответственно равна deg+ vi, deg– vi.
3) Пусть G =(V, E) – ориентированный мультиграф с непустым множеством дуг. Тогда
а) сумма строк матрицы BG является нулевой строкой,
б) любая строка матрицы BG является линейной комбинацией остальных строк;
в) ранг матрицы BG не превосходит | V |–1;
г) для любого контура в G сумма столбцов матрицы BG, соответствующих дугам, входящим в этот контур, равна нулевому столбцу.
4) Пусть G – мультиграф с непустым множеством ребер. Тогда при покоординатном сложении по модулю 2:
а) сумма строк матрицы BG является нулевой строкой
б) любая строка матрицы BG является суммой остальных строк;
в) для любого цикла в G сумма столбцов матрицы BG, соответствующих ребрам, входящим в этот цикл, равна нулевому столбцу.
Самостоятельно обоснуйте!
Рассмотрим матрицу 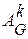 и обозначим ее элементы
и обозначим ее элементы  .
.
Теорема. Элемент 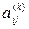 матрицы
матрицы  графа (орграфа) G =(V, E) равен числу маршрутов (путей) в G длины k, соединяющих вершину vi с вершиной vj (из вершины vi в вершину vj).
графа (орграфа) G =(V, E) равен числу маршрутов (путей) в G длины k, соединяющих вершину vi с вершиной vj (из вершины vi в вершину vj).
Самостоятельно обоснуйте!
Следствие. а) В n -вершинном графе (орграфе) G =(V, E) существует маршрут (путь), соединяющий вершину vi с вершиной vj (из вершины vi в вершину vj) Û элемент cij матрицы C = отличен от нуля.
отличен от нуля.
б) В n -вершинном графе (орграфе) G =(V, E) существует замкнутый маршрут (путь), проходящий через вершину vi Û элемент cii матрицы C = отличен от нуля.
отличен от нуля.
Замечание. Более экономичными в вычислительном отношении по сравнению с целочисленными матрицами являются булевы матрицы. Хранение их в памяти ЭВМ требует меньшего объема оперативной памяти, и логические операции над ними выполняются гораздо быстрее. Таким образом, устанавливать наличие (замкнутых) маршрутов (путей) в графе эффективнее обработкой булевых матриц.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 3098; Нарушение авторских прав?; Мы поможем в написании вашей работы!