Дифракция Френеля на простейших преградах

Дифракция от круглого отверстия. Поставим на пути сфериче­ской световой волны непрозрачный экран с вырезанным в нем круг­лым отверстием радиуса . Расположим экран так, чтобы перпен­дикуляр, опущенный из источника света 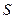, попал в центр отверстия (рис.3.3. 6). На продолжении этого перпендикуляра возьмем точку . При радиусе отверстия , значительно меньшем, чем указанные на рисунке длины 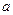и

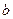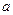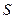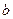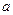, длину можно считать равной расстоянию от источника до преграды, а длину - расстоянию от преграды до точки . Если расстояния и 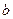удовлетворяют соотношению

,

где - целое число, то отверстие оставит открытыми ровно первых зон Френеля, построенных для точки .

Следовательно, число открытых зон Френеля определяется выражением

.

Амплитуда в точке будет равна

.

Перед берется знак плюс, если нечетное, и минус, если чет­ное. Положив выражения в скобках равными нулю, придем к формулам

(- нечетное),

(- четное).

Амплитуды от двух соседних зон практически одинаковы. Поэтому можно заменить через . В результате полу­чится

,

где знак плюс берется для нечетных и минус - для четных.

Для малых амплитуда мало отличается от . Следова­тельно, при нечетных амплитуда в точке будет приближенно равна , при четных - нулю.

Если убрать преграду, амплитуда в точке станет равной . Таким образом, преграда с отверстием, открываю­щим небольшое нечетное число зон, не только не ослабляет осве­щенность в точке , но, напротив, приводит к увеличению амплиту­ды почти в два раза, а интенсивности - почти в четыре раза.

Выясним характер дифракционной картины, которая будет наблюдаться на экране, помещенном за преградой (см. рис.3.3.6). Вследствие симметричного расположения отверстия относительно прямой освещенность в разных точках экрана будет

зависеть только от расстояния 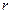от точки . В самой этой точке интенсивность будет достигать максимума или минимума в зависимости от того, каким - четным или нечетным - будет число открытых зон Фре­неля. Пусть, например, это число равно трем. Тогда в центре диф­ракционной картины получится максимум интенсивности. Картина зон Френеля для точки дана на рис. 3.3.7, а. Теперь сместимся по экрану в точку . Ограниченная краями отверстия картина зон Френеля для точки имеет вид, показанный на рис. 3.3.7, б. Края отверстия закроют часть третьей зоны, одновременно частично откроется четвертая зона. В итоге интенсивность света уменьшится и при некотором положении точки достигнет минимума. Если сместиться по экрану в точку 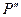, края отверстия частично закроют не только третью, но и вторую зону Френеля, одновременно от­кроется частично пятая зона (рис. 3.3.7, в). В итоге действие от­крытых участков нечетных зон перевесит действие открытых участ­ков четных зон, и интенсивность достигнет максимума, правда, более слабого, чем максимум, наблюдающийся в точке .

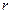Таким образом, дифракционная картина от круглого отверстия имеет вид чередующихся светлых и темных концентрических колец. В центре картины будет либо светлое (нечетное), либо темное (четное) пятно. Ход интенсивности с расстоянием от центра картины изображен на рис. 3.3.6,б (для нечетного ) и на рис. 3.3.6, в (для четного ). При перемещении экрана параллельно самому себе вдоль прямой картины, изображенной на рис.3.3.7, будут сменять друг друга (при изменении 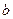значение становится то нечетным, то четным).

Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает. Если отверстие открывает большое число зон, чередование светлых и темных колец наблюдается лишь в очень узкой области на границе геометрической тени; внутри этой области освещенность оказывается практически постоянной.

Дифракция от круглого диска. Поместим между источником света 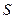и точкой наблюдения непрозрачный круглый диск радиуса (рис.3.3.8). Если диск закроет

первых зон Френеля, амплитуда в точке будет равна

Выражения, стоящие в скобках, можно положить равными нулю, следовательно,

.

Выясним характер картины, получающейся на экране (см. рис.3.3.8). Очевидно, что освещенность может зависеть только от рас­стояния 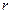до точки . При небольшом числе закрытых зон ампли­туда мало отличается от . Поэтому интенсивность в точке будет почти такая же, как при отсутствии преграды между источ­ником 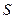и точкой . Для точки , смещенной относи­тельно точки в любом радиальном направлении, диск будет пере­крывать часть -й зоны Френеля, одновременно откроется часть -й зоны. Это вызовет уменьшение интенсивности. При неко­тором положении точки интенсивность достигнет минимума. Если сместиться из центра картины еще дальше, диск перекроет дополнительно часть -й зоны, одновременно откроется часть -й зоны. В результате интенсивность возрастет и в точке 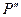достигнет максимума.

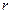Таким образом, в случае непрозрачного круглого диска ди­фракционная картина имеет вид чередующихся светлых и темных концентрических колец. В центре картины помещается светлое пятно. Изменение интенсивности света с расстоянием от точки изображено на рис.3.3.8, б.

Если диск закрывает лишь небольшую часть центральной зоны Френеля, он совсем не отбрасывает тени - освещенность экрана всюду остается такой же, как при отсутствии преград. Если диск закрывает много зон Френеля, чередование светлых и темных ко­лец наблюдается только в узкой области на границе геометриче­ской тени. В этом случае , так что светлое пятно в центре отсутствует, и освещенность в обла­сти геометрической тени практически всюду равна нулю. Если радиус диска во много раз больше радиуса закрытой им центральной зоны, то позади диска наблюдается обычная тень, у границ которой есть слабая интерференционная картина.

Дифракция от прямолинейного края полуплоскости. Поместим на пути световой волны (которую для простоты будем считать плоской) непрозрачную полуплоскость с прямолинейным краем. Расположим эту полуплоскость так, чтобы она совпала с одной из волновых поверхностей. На расстоянии 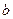за полуплоскостью поставим параллельный ей экран, на котором возьмем точку (рис. 3.3.9). Разобьем открытую часть волновой поверхности на зоны, имеющие вид очень узких прямолинейных полосок, парал­лельных краю полуплоскости. Ширину зон выберем так, чтобы отсчитанные в плоскости рисунка расстояния от точки до краев любой зоны отличались на одинаковую величину 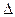. При этом условии колебания, создаваемые в точке соседними зонами, бу­дут отличаться по фазе на постоянную величину.

Зонам, расположенным справа от точки , припишем номера 1, 2, 3 и т. д., расположенным слева - номера 1', 2', 3' и т. д. Зоны с номерами и имеют одинаковую ширину и расположе­ны относительно точки симметрично. Поэтому создаваемые ими в колебания совпадают по амплитуде и по фазе.

Чтобы установить зависимость амплитуды от номера зоны , оценим площади зон. Из рис. 3.3.10 видно, что суммарная ширина первых зон равна

.

Вследствие узости зон . Поэтому при не очень больших квадратичным членом под корнем можно пренебречь. Тогда

.

Положив в этой формуле , получим, что . Следовательно, выражению для суммарной ширины первых зон можно придать вид

.

Отсюда

.

Расчет по последней формуле дает, что

.

В таких же соотношениях находятся и площади зон.

Из последнего соотношения вытекает, что амплитуда колебаний, создаваемых в точке отдельными зонами, вначале (для первых зон) убывает очень быстро, затем это убывание становится медленным. По этой причине ломаная линия, получающаяся при графическом сложе­нии колебаний, возбуждаемых прямолинейными зонами, идет сна­чала более полого, чем в случае кольцевых зон (площади которых при аналогичном построении примерно равны). На рис. 3.3.11 со­поставлены обе векторные диаграммы. В обоих случаях отставание по фазе каждого следующего колебания взято одним и тем же.

Значение амплитуды для кольцевых зон (рис.3.3.11, а) принято постоянным, а для прямолинейных зон (рис.3.3.11, б) - убываю­щим в соответствии с последним соотношением. Графики на рис.3.3.11 являются приближенными. При точном построении графиков нуж­но учитывать зависимость амплитуды от 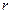и 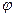. Однако на общем характере диаграмм это не отразится.

На рис.3.3.11, б показаны только колебания, обусловленные зонами, лежащими справа от точки . Зоны с номерами и расположены симметрично относительно . Поэтому естественно при построении диаграммы векторы, изображающие соответст­вующие этим зонам колебания, располагать симметрично относи­тельно начала координат 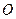(рис.3.3.12). Если ширину зон устре­мить к нулю, ломаная линия, изображенная на рис. 3.3.12, превра­тится в плавную кривую (рис. 3.3.13), которая называется спи­ралью Корню.

Дата добавления: 2014-01-04