Второе предельное состояние

Предельное условие f £ f_пред.

f_пред – функция назначения.

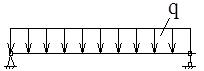
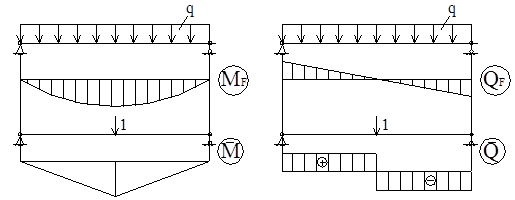
f – определяется по известным формулам строительной механики, например для шарнирно опертой балки при действии равномерно распределенной нагрузки:

f = f_M + f_Q + f_N

Особенности для балок:

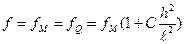
h – высота балки;

l – длина балки;

; f = 1,8f_М

Модуль сдвига для стали:

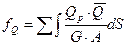
Для дерева

;

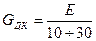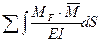
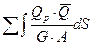
Расчет элементов ДК цельного сечения.

1. Центральное растяжение вдоль волокон.

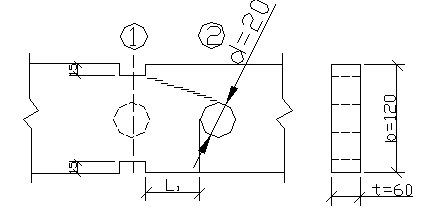
1. А_расч – зависит от растояния между ослаблениями.

Если совмещаем ослабления в одноя сечении.

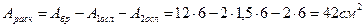
два ограничения для А_расч.

1. А_расч³50 см²;

2. А_расч³0,5А_бр.

Допускается ослабление но не более чем на половину сечения.

Характер разрушения: хрупкое; при разрушении концентраторы соединяются друг с другом по ступенькам (разрыв волокна – скалывание, разрыв волокна – скалывание и т. д.)

3. 2-й случай: 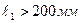- разрушение происходит по сечению с большим ослаблением.

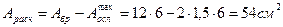
Те же ограничения для А_расч.

Коэффициент m₀: п. 3.2 он только учитывает наличие ослаблений.

m₀ = 1 – нет ослаблений.

m₀ = 0,8 – есть ослабления.

R_p = 12 МПа для клееного элемента (табл. 3) I сорт;

R_p = 9 МПа - II сорт.

2. Центральное сжатие вдоль волокон.

1. Прочность

2. Устойчивость

3. Ограничение гибкости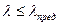

- основные;

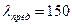- неосновные;

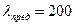- конструктивные элементы.

4. Ограничение площади А_расч³50 см²

Коэффициент продольного изгиба

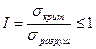
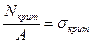
Упругая работа материала:

Для всех пород отношение 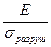принято постоянным 300;

IR = const ()

Предел применимости формулы Эйлера

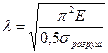
Упруго-пластическая работа материала

Формула Кочеткова в СНиП

Для стали используют формулу

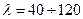
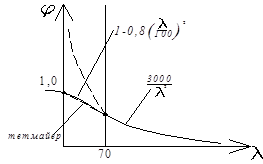
Расчетные длины

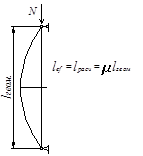
1.

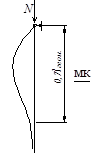
2.

В ДК трудно сделать жесткую заделку.

3.

4.

Радиус инерции.

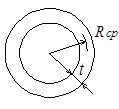Для круглой трубы

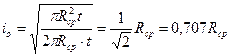
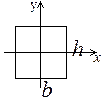
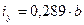
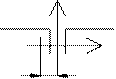Физический смысл радиуса инерции: (для расчета устойчивости) он показывает удаление материала от центра тяжести сечения.

Сечение 2-двух ветвевой колонны.

а – расстояние от оси до центра тяжести колонны

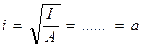
I=2Aa²

A=2A

Удельные характеристики:

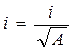Удельный радиус инерции:

(безразмерный параметр) для этого характеристики делят на площадь в какой – то степени, чтобы получить безразмерное число.

Удельный момент инерции: (момент сопротивления)

см⁴

см⁴

Удельный момент сопротивления

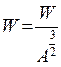см⁴

см⁴

Гибкость

больше на 20 – 3- % в ДК, чем в МК.

Расчетная площадь

А _расч. – см. примечания к табл. 3 СНиПа.

Площадь зависит от величины ослабления и места его расположения.

§ 3. Изгиб деревянных конструкций

1. Прочность:

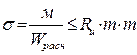
R_u=R_c табл. 3 СНиП

Также как и при растяжении ослабления расположенные на длине 200 мм совмещаем с дном сечения (см. раздел растяжения).

2. устойчивость при изгибе

φ_м ≤ 1 см. СНиП

φ_м зависит от (нагрузки) формы эпюры «М», закрепления концов балки и соотношения размеров: ширина, высота и т.д.

3. Ограничения по касательным напряжениям:

Важно для коротких балок

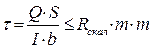
При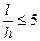

4. Ограничения по II предельному состоянию

f ≤ f_пред

f= f_м+ f_Q+ f_N; f_пред- т.16 СНиП

Для балки используем первые два слагаемых.

§ 4 Растяжения с изгибом

Пусть на стержень действует только продольная сила N, несущая способность будет обеспечена если:

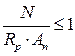
Пусть действует только изгибающий момент М, несущая способность будет обеспеченна если:

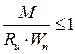
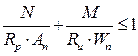при совместном действии N и М, несущая способность обеспеченна если:

перемножим все согласные на R_p и получим формулу СНиП:

Формула справедлива при любых соотношениях N и М и даёт погрешность в запас прочности до 20%.

§ 5 Сжатие с изгибом для балок или для стержней с изгибной жесткостью.

Аналогично разделу § 4 получим:

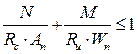
Перемножим все слагаемые на R_C = Ru и получим:

погрешность в запас до 6%.

§ 6 Сжатие с изгибом для стержней

Рассмотрим шарнирно опёртый стержень под действием нагрузки q:

f₀ – максимальный прогиб.

К стержню в деформированном состоянии приложим продольную силу N.

Ось стержня получит дополнительное перемещение, максимальный прогиб – f_n. Пусть изогнутая ось стержня будет синусоидой при действии только нагрузки q, а также при совместном действии q и N.

(1)

Задача решается в рядах Фурье, но с использованием только первого члена ряда. Полный момент от действия q и N будет равен:

(2) M_nx = M_qx + N × f _nx – учёт деформированной оси.

Дифференцированное уравнение изогнутой оси балки:

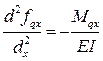(3)

Разделим все слагаемые уравнения (2) на EI

(4)

Заменим все слагаемые их частными производные:

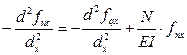(5)

Продифференцируем выражение (1) два раза и запишем в формулу (5)

(6)

Сократим sin; разделим все слагаемые в формуле (6) на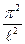

(7)

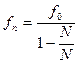
(8)

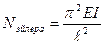
- Эйлерова критическая сила

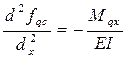Выразим f₀ через M и N, для этого запишем:

(9)

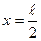
(10)

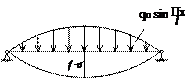
Поставим значение f_n = f₀ / _ξ; ; 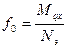в формулу (2) и после простых преобразований 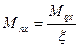(11)

ξ - учитывает увеличение изгибающего момента или увеличение прогиба за счет деформации оси стержня при совместном действии q и N.

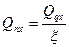(12) перерезывающая сила.

Расчётная формула при сжатии с изгибом деревянного стержня:

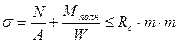
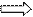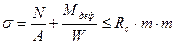СНиП (13)

Ограничения для ξ

1) 0< ξ <1

;

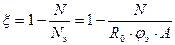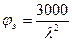
ξ – получено правильно только для упругой работы материала (при λ > 70)

При λ < 70определяется ξ приближённо.

Приступая к расчету, можем задаться малой площадью А и получим большое λ, так, что слагаемое 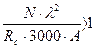, а ξ станет «–» - отрицательным, что не имеет физического смысла. В этом случае увеличиваем А, пока ξ станет > 0.

2) если доля изгиба очень мала , то требуется дополнительная проверка по формуле центрально-сжатого стержня, (например для безмоментной арки)

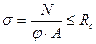
3) Если нагрузка отличается от плавной (распределённой или синусоидной), например в виде сосредоточенных сил или моментов, тогда ξ = ξ × К_н, К_н- поправочный коэффициент в СНиПе.

4) При действии произвольной нагрузки поперечной раскладываем нагрузку на

прямосиметричную и кососиметричную.

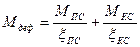
М _деф – момент с учетом деформированной схемы.

Формула (13) – это формула прочности, мы имеем напряжение краевые с учетом деформируемой схемы. По этой формуле проверяют прочность рам, куполов, арок, верхних поясов ферм и т.д., но она сделана только для упругой работы стержня.

Дата добавления: 2014-01-04