Метод простого перебору

Задається послідовність точок:

,

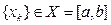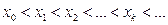
Наприклад: 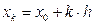(k=0,1,2,…)

h=const>0

Після цього послідовно визначаються значення функцій 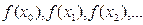, і це продовжується доти, доки не знайдеться таке k, що:

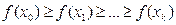, але 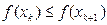, тоді зрозуміло що отримане рішеня буде лежати на відрізку 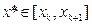, тобто на відрізку локалізації мінімуму

Для уточнення точки мінімуму можна повторити процедуру на відрізку 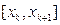з малим шагом .

Висновок: Цей метод достатньо неточний, може бути трудоємким, на практиці його використовують для визначення значення функції f(x) і знаходження точки мінімуму.

2. Метод дихотомії (ділення відрізку навпіл)

Нехай N=2k (число ітерацій алгоритму парне), на відрізку [a,b] вибираємо 2 точки:

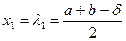
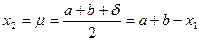
де ,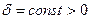

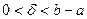
Величина 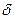обирається обчислювачем і може характеризувати похибку визначення величини x і обмежена знизу можливостями обчислювального апарату.

b

a

δ

Точки 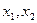розміщені симетрично на відрізку [a,b] відносно його середини і при малих 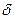розділяє його майже навпіл, цим пояснюється назва методу, далі визначаємо і порівнюємо значення функції та .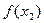

Якщо f(x1)≤f(x2) – то вважаємо що:

а2=а; в2=м1

Якщоf(x1)>f(x2) – то вважаємо що:

а2=£1; в2=в

В результаті отримаємо відрізок локалізації [ a2;b2], довжини:

в2-а2 = 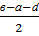+ɗ

Нехай відрізок локалізації мінімальний вже побудований і довжина його:

Bk-ak=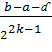+ɗ

Тоді беремо точки:

£k=

µ=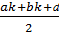

Вираховуєм: f(£k) и f(µk) і отримуємо відрізок: [ak+1; bk+1]

Bk+1-ak+1=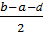+ɗ>0

Якщо кількість обмежених значень функції не чим не обмежена, то описаний процес ділення відрізка навпіл, можна продовжувати до тих пір поки не вийде відрізок довжиною:

Bk+1-ak+1<E

E-задана точність; Е>ɗ,тоді:

K>log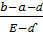-1

Якщо кількість обмежень значемості функції не чім не обмежена, то описаний процес ділення відрізка навпіл, можна продовжувати до тих пір поки не вийде відрізок довжиною:

Bk+1-ak+1<E,тоді:

N=2k>2log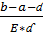

Наближене рішення задачі XN можна вибрати таким способом:

XN=£k f(£k)<f(µk)

XN=µk f(£k)>f(µk)

А значення в точці: F(XN)~f(X*)

При такому виборі наближення до точки мінімуму буде допущена похибка:

F(XN)~f(X*)

Як наближення до оптимального рішення можна вибрати середину відрізка і похибка буде менше.

3) Метод «Золотого перетину»

Золотим перетином відрізка називається розподіл відрізка на 2 частини так, що відношення довжини всього відрізка до лине здебільшого = відношенню довжини більшої частини до меншої.

Золотий перетин відрізка [a, b] виробляють 2 симетрично розташовані відносно середини відрізка [a, b] точки х1 і х2:

а х1 х2 в

х1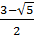=а+(в-а)

х2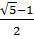=а+(в-а)

Чудово те, що точка х1 в свою чергу виробляє золотий перетин відрізка [a; x2], точка х2 золотий перетин відрізка [x1; b].

Припустимо: а1 = а; в1 = в,

Обчислюємо значення функцій: f (x1), f (x2)

Якщо: F(x1)≤f(x2)=>a2=a1,b2=x2

Якщо: F(x1)>f(x2)=>a2=x1,b2=b1

Отримуємо відрізок: [a2, b2] довжини, що містить точку мінімуму f в точці х2 і значення f (x2):

B2-a2=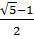(b-a).

Припустимо, що вже визначені точки:

Х1,х2,…….хn и найдём отрезок [an,bn] довжини:

Bn-an=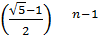(b-a)

Містить точку мінімуму xƐ [an, bn] і точку хn - виробляє золотий перетин відрізка [an, bn]:

F(xn)=minf(x2)

Тоді в якості наступної точки беремо: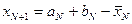

У результаті отримаємо відрізок: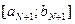

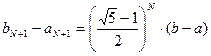
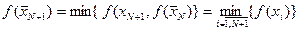
Якщо N не обмежено, то критерій зупинки довжина відрізка менша заданої точності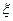

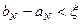
Дата добавления: 2014-01-04