Одноетапні задачі СП

Якщо.

5) критерій опуклості в термінах других похідних.

Теорема: Двічі диференціальна на 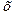функція, опукла тоді і тілько тоді, коли:

Умова (4) означає, що матриця Гессе 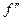негативно визначена для всіх .

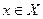Властивість (5) в комбінації з критерієм Сильвестра складе зручний апарат для перевірки опуклості функції невеликого числа змінних, тоды обчислення мінорів не складе великих зусиль.

Приклад: Визначити чи є функція 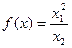опуклою на множині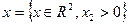

;

;

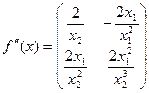з критерію Сильвестра слідує що функція 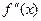не відьємно визначена, це значить що функція опукла.

Зауваження: Доказ цього факту на основі визначення, привело б до досить громіздким викладки.

6) Кожен локальний мінімум функції 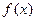на опуклій множені є глобальним.

7) Строго опукла функція 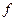на опуклій множені досягає мінімуму в єдиній точці.

Зауваження 1: обмеження типу рівності (4) можна легко звести до системи нерівностей 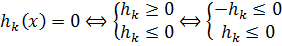(3)

ми можемо говорити про завдання (2), (3), (5)
Для формулювання умов існування локального мінімуму або максимуму функції f (x) на множині Ω введемо функцію Лагранжа, для задачі (2), (3), (5).

Max:

(6)

Min:

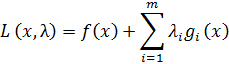(7)

λͥ ≥0; i=1,m

коефіцієнт λ ͥ - множники Лагранжа.
Для задачі (2), (3), (5) умов оптимізації множників Лагранжа можна надати Економічний сенс:
Якщо функція f (x) = f (x1,..., xn) - це дохід відповідний планом х = (х1,..., хn), а функція gi (x) - це витрати i-ого ресурсу характеризуються зміна екстремального значення цільової функції при зміну i-ого ресурсу (нескінченно малим або одиничним) - маргенальние або двоїсті оцінки.
Завдання (2), (3), (5), називається задачею опуклого програмування, якщо функція f (x) опукла вгору для завдання на максимум (опукла вниз для завдання на мінімум) функції gi (x)
опуклі вниз і безліч Х опукло.
Точка (х *; λ *) - є сідлової точкою функції Лагранжа, якщо для завдання на максимум виконується нерівність:

max: L(x; λ*)≤L(x*; λ*)≤L(x*; λ) (8)

min: L(x*; λ)≤L(x*; λ*)≤L(x; λ*) (9)

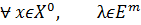
Питання, який зв'язок між сідловою точкою функції Лагранжа і оптимальним рішенням задачі (2), (3), (5).
Теорема 2. Нехай (x *; λ *) - сідлова точка функції Лагранжа в х0, λ ≥ 0, тоді х * є рішенням задачі (2), (3), (5), при чому виконується умова доповнюються не жорсткості, тобто (10)

Зауваження 2: не для будь-якої, навіть опуклої задачі (2), (3), (5) відповідна функція Лагранжа має сідлову точку.
Приклад. f (x) =-x → min
g (x) = x ² ≤ 0; x ≥ 0
очевидно, що це завдання є опуклою, так само очевидно, що безліч допустимих рішень Ω = {0} => f (x *) = 0
Побудуємо відповідну функцію Лагранжа
L (x; λ) =- x + λx ², λ ≥ 0, x ≥ 0
Ця функція не має сідлової точки-це пояснюється тим, що в цьому випадку допускається безліч Ω не задовольняє вимогу регулярності.
Обмеження gi (x) = 0, називається регулярним на безлічі х ˚, якщо існує х ~ є х ˚, gi (x ~) <0 (11)
Безліч Ω = {x: gi (x) ≤ 0, i = 1, m}, називається регулярним, якщо регулярні всі обмеження gi (x) ≤ 0, i = 1, m.
Іншими словами безліч Ω містить внутрішню точку, при цьому вважається, що для задачі (2), (3), (5) виконується умова регулярності Слейтера.
Теорема 3. (Куна-Таккера).
Нехай задача (2), (3), (5), є завданням опуклого програмування, при чому, виконується умова регулярності Слейтера, тоді х * є вирішенням завдання в тому і тільки втом випадку, якщо існує λ *> 0, що (х *; λ *) - сідлова точка функції Лагранжа.
Зауваження 3. Незважаючи на те, що теорема Куна-Таккера не дає методу пошуку оптимального рішення, вона має велике теоретичне значення, в тому числі і для розробки методів розв'язання задач умовної нелінійної оптимізації. Теорема показує, що пошук точки умовного мінімуму або максимуму можливо при певних припущеннях можна звести до задачі знаходження сідлової точки функції Лагранжа, тим самим процес рішення задачі безумовної оптимізації.
Так само теорема Куна-Таккера має значення для розробки методики вирішення завдань квадратичного програмування.
Уточнення умови Куна-Таккера.
Проаналізуємо умова дозволу задачі нелінійного програмування.
max f (x) (12)
gi (x) ≤ bi, x ≥ 0 (13)
Розглянемо завдання на max функції f (x) з умовою тільки невід'ємних змінних х ≥ 0, х = (х1,..., хn), хєE ^ n
Необхідна умова локального максимуму є (2n +1) умови:

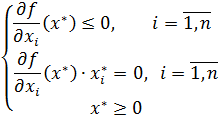
Перейдемо до задачі (12): умови теореми Куна-Таккера, які є необхідною умовою дозволу в задачі нелінійного програмування:

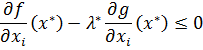
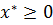(n) (m)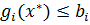

λ*<b-g(x*)>=0 (m) λ*≥0

Стохастичне програмування

Поняття про стохастичних задачах і стохастичному програмуванні.
Задачі оптимізації та їх моделі, які розглядалися раніше, містять припущення, що вся початкова інформація задана строго однозначно. Такі задачі моделювання, називаються детермінованими. Насправді, детерміновані моделі виявляються неадекватними в реальному світі.
Основна причина цього: неповнота, неточність даних на основі яких будується модель.
Стохастичне програмування (СП) - це розділ математичного програмування, який вивчає теорію та методи вирішення проблеми прийняття оптимального рішення в умові ризику невизначеності, при необхідності врахування впливу випадкових факторів.

Зауваження. Ситуації з ризиком – ситуації, коли параметри моделі мають імовірнісний характер. Ситуації з невизначеністю – ситуації, коли наявна інформація не створює певної уяви про характер зміни параметрів.

Рішення задач за недостатньої інформації призводить до зниження економічної ефективності рішень, що приймаються.

Види стохастичного програмування:

1. Пасивне – сукупність прийомів, що дозволяють знаходити найкраще рішення та екстремальні значення цільової функції в оптимізаційних задачах з випадковими початковими даними (при цьому використовуються, зокрема, ідеї параметричного програмування).

2. Активне – сукупність прийомів, що дозволяють розвивати методи вибору рішення в умовах ризику і невизначеності.

В стохастичному програмуванні використовують одно-, дво- та багатоетапні задачі.

Роздивимось типові задачі нелінійного програмування:

Знайти таке рішення для якого

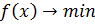(1)

(2)

(3)

Задачі стохастичного програмування виникають у випадках, коли функції 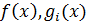залежать також від випадкових параметрів ω.

При цьому передбачається, що ω є елементом станів природи чи випадкових параметрів ().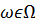

Тоді задачі стохастичного програмування можна сформулювати:

(4)

(5)

(6)

Постановка задач стохастичного програмування залежить від того, чи є можливість при виборі рішень уточнити стан природи шляхом деяких спостережень чи ні. У зв’язку з цим розрізняють задачі:

- оперативного стохастичного програмування;

- перспективного стохастичного програмування.

Оперативне стохастичне програмування – рішення х приймається після деякого експерименту над станом природи ω. Це рішення залежить від результатів експерименту і являє собою випадковий вектор х=х(ω).

Такі задачі виникають, наприклад, в оперативному техніко-економічному плануванні, медичній діагностиці та ін.

Перспективне стохастичне програмування – рішення х приймаються до проведення яких-небудь експериментів над станом природи і тому саме рішення є детермінованим.

Такі задачі виникають в перспективному техніко-економічному плануванні, в задачах проектування (коли параметри системи вибираються з певних компонент).

Задачі стохастичного програмування зазичай задаються в одній з наступних форм:

А) знайти 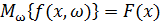(7)

за умов (8)

Б) знайти 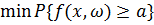(9)

за умов (10)

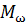– операція математичного очікування;

P – імовірність;

a, 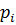– деякі дійсні числа.

Можливі деякі комбінації задач: (7)-(8) та (9)-(10). Наприклад, знайти min (7) за умов (10) чи знайти min (9) за умов (8).

Не дивлячись на можливі відмінності в постановках задач (7)-(8) та (9)-(10), вони можуть бути зведені до деякого загального формулювання, наприклад виду (7)-(8).

Для цього необхідно ввести наступні характеристики функції:

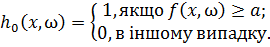(11)

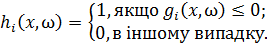(12)

Для цих функцій

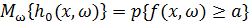
Тоді (9)-(10) зводиться до:

знайти 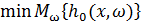(13)

за умов 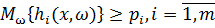(14)

Існує два підходи рішення задач стохастичного програмування:

1) непрямі методи: полягають у знаходженні функції f(x), 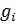(x) та рішенні еквівалентних детермінованих задач виду (7)-(8).

Зауваження. Такий підхід застосовується лише в обмеженій кількості випадків.

2) прямі методи засновані на інформації про значення функцій f(x,w) та g(x,w), а в результаті оптимізації експериментів.

До одноетапних задач СП відносяться задачі, в яких рішення приймаються на основі відомих стохастичних характеристик розподілу випадкових параметрів.

Рішення приймаються до спостереження за реалізацією поточного значення цих параметрів.

При цьому повинне прийматися деяке найкраще в середньостатистичному сенсі рішення.

Постановки задач СП відрізняються за трьома ознаками:

1) за характером рішення

2) за вибором показника рішення

3) за способом розчленування обмежень задачі

В якості умов і функцій в задачах СП з ймовірнісними обмеженнями зазвичай приймаються такі функціонали як:

а) системне очікування

б) дисперсію цільової функції

в) ймовірність перевищення його деякого порогу

Приклади задач:

1) задачі з ЦФ виду

M(C^Т X), називаються М-моделями

2) Задачі, в яких вимагаються мінімальні величини дисперсії

D(C^Т X) = M(C^Т X – C^-T X)², називаються V-моделями.

3) Задачі, в яких мінімізується ймовірність

Р{ C^Т X ≥ C^Т X₀ = k},називається Р-моделями

В ці ж групи включені також задачі, в яких вимагається мінімізувати поріг k, який не повинен бути вищий мінімальної форми з заданою ймовірністю α.

k→min Р{ C^Т X ≤ k}= α

Обмеження задачі можуть бути представлені в одній із наступних форм запису:

1) 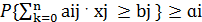0 ≤ α_i ≤ 1 i= 1,n

2) P { Ax ≥ B } ≥ α_i 0 ≤ α_i ≤ 1 i= 1,n

3) P {Z a_ij · x_j ≥ b_ik, i_k є I_k } ≥ α_k 0 ≤ α_k ≤ 1 k= 1,n

Розглянемо задачу лінійного стохастичного програмування з ймовірнісними обмеженнями:

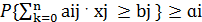i = 1,m (2)

x_j ≥ 0 j = 1, n (3)

При детермінованій матриці

А=(a_ij)

b=(b₁,..b_i,.., b_n)

Задача (1)-(3) зводиться до еквівалентної детермінованої ЗЛП наступним чином:

Нехай Р(b₁,..b_i,.., b_n) – спільна щільність розподілу складових b_i випадкового вектору b. Знайдемо щільність розподілу b_i

P_i (b_i) = ⌠^∞_-∞ …⌠^∞_-∞ P (b₁, b₂, …, b_m) db₁, db₂…db_i-1,db_i+1,…db_m

Обчислимо b_i^* з

⌠^∞_bi P_i (b_i) db_i = α_i i = 1, m (4)

Якщо рішення рівняння (4) не єдине, то якості b_i найбільший корінь.

Очевидно, що умова (2)

∑ⁿ_j=1 a_ij · x_j ≤ b_i^*

де b_i^{* -} задовольняє умові (4)

відповідно, задача СП виду (1) – (3) буде еквівалента наступній детермінованій задачі

C^-T X→max (5)

де С*=М(С) – мат. очікування

b_i^* – корінь рівняння F(b_i^*) = 1 – α_i, відповідно, b_i^* = F_i^-1 (α - α_i)

F (b_i^*) – функція розподілу випадкової величини b_i.

Приклад. Крупна свиноферма має можливість купувати від 1 до 4 різних видів зерна і готувати різні види сумішей. Різні зернові культури складаються з різної кількості поживних компонентів. Нехай в розрахунок приймається 4 компоненти:

А – білок

Б – жири

В – вуглеводи

Д – вітаміни

Вихідні дані задачі в табл. 1

Інгредієнти в складі сумішей	Склад інгредієнтів в 1-ці виду зерна	Мін. спожив. на план. раціон
3. - 1	3. - 2	3. - 3
А
В
С
Д	0,6	0,25		232,5

Управляючим встановлено, що комбікорм для свиней повинен відповідати деяким лінійним вимогам з точки зору поживності.

Питомі затрати на одиницю ваги зерна 31, 32, 33 складають відповідно 41, 35, 96.

Вимоги визначають для певних сумішей кількість зерна кожного виду.

Нам необхідно знайти такий вектор х=(х₁, х₂, х₃) при якому ЦФ

f(x) = 41x₁ + 35x₂ + 96x₃ → min

і обмеженнях

2х₁ + 3х₂ + 7х₃ ≥ 1250

х₁ + х₂ ≥ 2500

5х₁ + 3х₂ + 6х₃ ≥ 900

0,6х₁ + 0,25х₂ + х₃ ≥ 232,5

Дата добавления: 2014-01-04