
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алфавит логики высказываний
|
|
|
|
Логика высказываний
Введение
Существует шесть аспектов, однозначно и функционально полно определяющих исчисление как математическую структуру:
1) алфавит исчисления:
2) правила образования языка в алфавите - синтаксис языка;
3) правила присвоения истинностных значений формулам - семантика языка;
4) правила вывода в исчислении, т.е. правила, определяющие корректный (сохраняющий отношение логического следования) переход от одних теорем к другим, с одной стороны, и формализующие определенные стандартные способы рассуждений – с другой;
5) правила эквивалентного преобразования форму исчисления;
6) алгоритмы, эффективно распознающие достоверность рассуждений.
Исторически исчисление предикатов выросло из логики высказываний, являющейся составной частью логики предикатов. Поэтому вначале рассмотрим в указанных аспектах логику высказываний, а затем перейдем к логике предикатов.
Элементами (символами) алфавита являются:
Ø высказывания, обозначаемые строчными буквами;
Ø пять логических связок (табл.3.1)
Таблица 3.1
| Название связки | Обозначение | Тип | Другие обозначения |
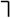  Отрицание Отрицание
| Унарный | , ~, not, не | |
 Конъюнкция Конъюнкция
| Ù | Бинарный | &,, and, и |
| Дизъюнкция | Ú | Бинарный | /, or, или |
| Импликация | É | Бинарный | Þ, ® |
| Эквивалентность | º | Бинарный | ó, «, ~ |
Высказывание–это повествовательное (утвердительное) предло-жение, о котором можно сказать истинно оно или ложно (True or False).
Примеры[12]:
1. Идет дождь. Это предложение является высказыванием, и его можно заменить (идентифицировать) буквой q.
2. Дорога мокрая. Это тоже высказывание, и его можно идентифицировать буквой r.
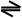 В дальнейшем процесс идентификации высказывания определенной строчной буквой будем обозначать символом (равно по определению).
В дальнейшем процесс идентификации высказывания определенной строчной буквой будем обозначать символом (равно по определению).
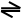
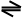
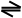 3. p Снег белый. h Президент уходит в отставку.
3. p Снег белый. h Президент уходит в отставку.
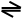 e Земля вертится. n Длина окружности равна её диаметру.
e Земля вертится. n Длина окружности равна её диаметру.
Следует обратить внимание на то, что в высказывании представляется взаимосвязь (отношение) отражаемого объекта с его свойствами или характеристиками, или какими-либо действиями объекта, или рассматривается взаимосвязь двух или большего количества отражаемых объектов. Это важно для понимания семантики термина ‘‘предикат‘‘, например,
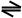 4. k Сторона b, сторона a, сторона c являются сторонами равнобедренного треугольника T.
4. k Сторона b, сторона a, сторона c являются сторонами равнобедренного треугольника T.
В логике высказывания действуют два соглашения:
1) Заключение об истинности (И) или ложности (Л) конкретного высказывания даёт субъект, моделирующий реальный мир, при постановке и решении некоторой задачи. Семантика отражаемого высказывания и представления об её истинности полностью определяется моделью мира этого субъекта. Разные субъекты могут иметь разные модели реального мира.
2) В основу логики высказываний положено дедуктивное рассуждение, поэтому она имеет и другое название - ‘‘исчисление высказываний‘‘. Вернуться
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1592; Нарушение авторских прав?; Мы поможем в написании вашей работы!