
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предикатов
|
|
|
|
Доказательство теорем методом резолюций в логике
Не существует четких правил и рекомендаций, как представить в виде формулы логики предикатов то или иное умозаключение. Все это делается интуитивно. А интуиция находится в пропорциональной зависимости от мастерства в доказательстве теорем методом резолюций. Поэтому только через практику и навыки можно приобрести необходимую интуицию для моделирования умозаключений. В какой-то мере стартовую интуицию можно приобрести, ознакомившись с приведенными ниже примерами, рассмотренными в различных работах [4,6,7,11,12]. В первых двух примерах приводятся достаточно подробные объяснения, в остальных – только по мере надобности.
Пример 1. Некоторые пациенты любят своих докторов. Ни один пациент не любит знахаря. Следовательно, никакой доктор не является знахарем.
Введем следующие обозначения для предикатных символов: 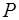 - пациент,
- пациент, 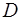 - доктор,
- доктор, 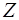 - знахарь,
- знахарь, 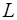 - любит.
- любит.
Тогда перечисленные ниже предикаты будут обозначать:
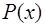 —
— 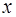 есть пациент;
есть пациент;
 —
— 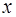 есть доктор;
есть доктор;
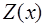 —
— 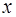 есть знахарь;
есть знахарь;
 —
— 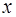 любит
любит  .
.
Факты и заключение, приведенные в рассуждении, могут быть представлены следующими формулами:
Факт 1 
 Факт 2
Факт 2 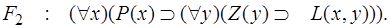
 Заключение
Заключение 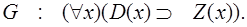
 В соответствии с условиями эффективного доказательства теорем методом резолюций преобразуем факты
В соответствии с условиями эффективного доказательства теорем методом резолюций преобразуем факты  ,
,  и отрицание заключения
и отрицание заключения  по правилам эквивалентных преобразований в следующие дизъюнкты:
по правилам эквивалентных преобразований в следующие дизъюнкты:
|
|
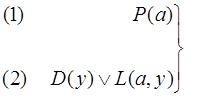

|



 из
из 
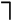
|

Выполняя унификации и склейки, получим:
 резольвента (2) и (4).
резольвента (2) и (4).


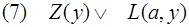 резольвента (1) и (3).
резольвента (1) и (3).
 резольвента (5) и (7).
резольвента (5) и (7).


 резольвента (6) и (8).
резольвента (6) и (8).
Теорема доказана.
Пример 2. Все люди – животные. Следовательно, голова человека является головой животного.
Пусть есть следующие предикаты:
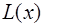 —
— 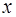 есть человек;
есть человек;
 —
— 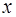 есть животное;
есть животное;
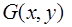 —
— 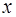 является головой
является головой  .
.
Необходимо доказать теорему:


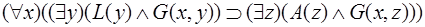
Преобразование числителя (теоремы-посылки) дает дизъюнкт:
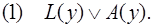
Для получения остальных дизъюнктов преобразуем отрицание знаменателя (теоремы-заключения) следующим образом:



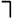

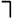


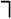

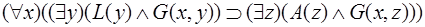


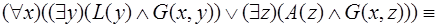

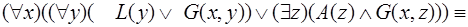

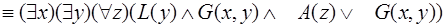 .
.
Тогда 
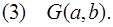

Применяя метод резолюций, получим:
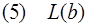 из (1) и (2).
из (1) и (2).
 из (4) и (5).
из (4) и (5).

 из (3) и (6).
из (3) и (6).
Теорема доказана.
Пример 3. Посылки: таможенные чиновники обыскивают каждого, кто въезжает в страну, кроме высокопоставленных лиц. Некоторые лица, способствующие провозу наркотиков, въезжают в страну и обыскиваются исключительно людьми, также способствующими провозу наркотиков. Никто из высокопоставленных лиц не способствовал провозу наркотиков.
Заключение: некоторые из таможенников способствовали провозу наркотиков.
Введем следующие обозначения для предикатов:
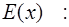
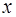 въезжал в страну;
въезжал в страну;
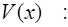
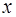 был высокопоставленным лицом;
был высокопоставленным лицом;

 обыскивал
обыскивал 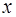 ;
;

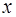 был таможенником;
был таможенником;

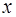 способствовал провозу наркотиков.
способствовал провозу наркотиков.
Посылки представляются следующими формулами:
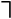


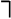
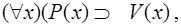
а заключение теоремы – формулой:

Преобразуя посылки в дизъюнкты, получим:




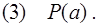


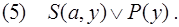

Отрицание заключения:



Доказательство методом резолюций выглядит следующим образом:

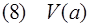 из (3) и (6).
из (3) и (6).
 из (2) и (4).
из (2) и (4).
 из (8) и (9).
из (8) и (9).
 из (1) и (4).
из (1) и (4).
 из (8) и (11).
из (8) и (11).
 из (12) и (5).
из (12) и (5).
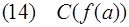 из (7) и (13).
из (7) и (13).

 из (10) и (14).
из (10) и (14).
Заключение доказано.
Пример 4. Существуют студенты, которые любят всех преподавателей. Ни один из студентов не любит невежд. Следовательно, ни один из преподавателей не является невеждой.
Обозначим:
 —
— 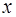 есть студент;
есть студент;
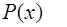 —
— 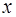 есть преподаватель;
есть преподаватель;
 —
— 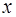 есть невежда;
есть невежда;

 —
— 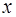 любит
любит  .
.
На языке логики предикатов после приведения к стандартному виду это запишется так:



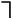

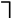
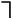




Преобразование двух теорем-посылок числителя дает следующие дизъюнкты:
 .
.


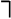
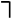


После преобразования отрицания заключения из знаменателя получим:
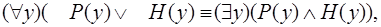 что дает дизъюнкты:
что дает дизъюнкты:
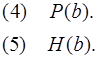
Путем унификации и склеек получим:
 из (2) и (4).
из (2) и (4).
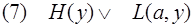 из (1) и (3).
из (1) и (3).

 из (5) и (7).
из (5) и (7).

 из (6) и (8).
из (6) и (8).
Теорема доказана.
Пример 5. Задача об обезьяне и банане.
Обезьяна хочет съесть банан, подвешенный к потолку комнаты. Рост обезьяны недостаточен, чтобы она могла дотянуться до банана. Однако она может ходить по комнате, переносить стул, находящийся в той же комнате, может забраться на стул и достать банан. Показать порядок действий обезьяны, при котором она достанет банан.
Предикаты здесь такие:
 означает, что в состоянии
означает, что в состоянии  обезьяна находится в точке
обезьяна находится в точке 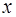 , банан - в точке
, банан - в точке  , а стул – в точке
, а стул – в точке 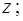
 означает, что в состоянии
означает, что в состоянии  обезьяна может достать банан.
обезьяна может достать банан.
Функции, участвующие в описании задачи, следующие:
ходить  - состояние, которое получается, если обезьяна находилась сначала в состоянии
- состояние, которое получается, если обезьяна находилась сначала в состоянии  и перешла из точки
и перешла из точки 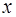 в точку
в точку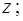
носить  - состояние, которое получается, если обезьяна находилась сначала в состоянии
- состояние, которое получается, если обезьяна находилась сначала в состоянии  и перешла из точки
и перешла из точки  в точку
в точку  , неся с собой стул;
, неся с собой стул;
взбираться  - состояние, которое получается, если обезьяна находилась в состоянии
- состояние, которое получается, если обезьяна находилась в состоянии  и влезла на стул.
и влезла на стул.
Предполагаем, что первоначально обезьяна находилась в точке 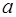 , банан – в точке
, банан – в точке 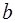 , стул – в точке
, стул – в точке 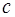 и обезьяна была в состоянии
и обезьяна была в состоянии  .
.
Таким образом, имеем следующие аксиомы:




 ходить
ходить 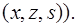
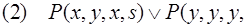 носить
носить 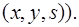
 взбираться
взбираться 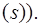
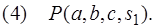
Здесь дизъюнкт (1) означает, что в любом состоянии обезьяна может перейти из точки 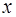 в точку
в точку 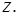
Дизъюнкт (2) означает. Что если обезьяна находится около стула, который стоит в точке 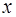 , то она может перенести его в любую точку
, то она может перенести его в любую точку  .
.
Дизъюнкт (3) означает, что если стул и обезьяна находятся под бананом, то обезьяна может влезть на стул и достать банан.
Дизъюнкт 4) описывает исходную ситуацию.
Заключению теоремы соответствует дизъюнкт
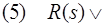 ответ
ответ  .
.
В этом дизъюнкте предикат ответ требует установить порядок действий обезьяны, соответствующий состоянию обезьяны с бананом.
Используя дизъюнкты (1) — (5), выводим следующие резольвенты:

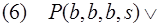 ответ (взбираться
ответ (взбираться 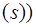 из (5) и (3).
из (5) и (3).
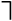

 ответ (взбираться (носить
ответ (взбираться (носить  из (6) и (2).
из (6) и (2).
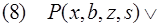 ответ (взбираться (носить
ответ (взбираться (носить 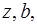 ходить
ходить 
из (7) и (1).
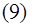 ответ (взбираться (носить
ответ (взбираться (носить  ходить
ходить  из (8) и (4).
из (8) и (4).
Дизъюнкт (9) дает ответ. Его можно интерпретировать как выполнение следующих действий (начиная с самой внутренней функции в дизъюнкте (9) и двигаясь наружу):
1. Обезьяна идет из точки 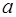 в точку
в точку 
2. Обезьяна идет из точки 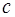 в точку
в точку 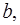 неся с собой стул.
неся с собой стул.
3. Обезьяна влезает на стул.
После этих действий обезьяна достает банан.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 385; Нарушение авторских прав?; Мы поможем в написании вашей работы!