Процесс обработки данных

Обработка – процесс преобразования информации к такому виду, из которого можно получить знание.

Преобразования, производимые в процессах сбора, передачи и хранения (кодирование, сжатие и т.д.) – это перезапись одной и той же информации, представление ее в разных формах. Ничего нового из этой информации не появляется. В процессе же обработки из имеющейся информации появляется нечто новое.

Пример 1.1. Митя и Алеша вместе собрали 40 грибов. Митя собрал на 10 грибов больше, чем Алеша. Сколько грибов собрал каждый мальчик?

Для того чтобы ответить на этот вопрос, надо решить систему уравнений:

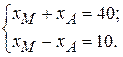(1.1)

Решить ее, т.е. обработать данную информацию, можно, например, методом Крамера.

Шаг 1. Вычислим определитель матрицы системы D = 1×(–1) – 1×1 = – 2. Он не равен 0, значит, система имеет решение.

Шаг 2. Вычислим определители для каждого неизвестного: D _А = 10 – 40 = – 30; D _М = – 40 – 10 = – 50.

Шаг 3. Вычисляем каждое неизвестное: ;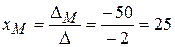

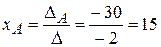
Ответ: Митя собрал 25 грибов, а Алеша – 15.

Иными словами, процесс обработки информации состоит из отдельных шагов. В результате выполнения каждого шага возникает порция новой информации.

Как было сказано в п. 1.1, описание пошагового процесса обработки информации называется алгоритмом.

Более подробно об алгоритмах поговорим в следующей теме.

Тема 2. Алгоритмизация и программирование

2.1. Алгоритм и его свойства

Что такое алгоритм. <TBODY>Алгоритм – точная и понятная инструкция исполнителю совершить некую последовательность действий, направленных на решение поставленной задачи. </TBODY>

Название "алгоритм" произошло от латинской формы имени среднеазиатского математика аль-Хорезми – Algorithmi, написавшего популярную в эпоху средневековья книгу о правилах выполнения арифметических действий, т.е. об алгоритмах вычисления произведения, частного и т.д.

<TBODY>Исполнитель алгоритма — это некоторый абстрактный (воображаемый) или реальный объект, способный выполнить действия, предписываемые алгоритмом. В информатике универсальным исполнителем алгоритмов является компьютер.

Основные свойства алгоритма. Слова “инструкция” или “предписание” близки по смыслу слову “алгоритм”, однако они не тождественны ему. Дело в том, что не всякая инструкция может быть названа алгоритмом, поскольку он должен обладать рядом обязательных свойств, которыми произвольное предписание обладать не обязано. Перечислим эти свойства.

1) Конечность – любой алгоритм должен заканчиваться после выполнения конечного (т.е. не бесконечного) числа шагов.

Если алгоритм содержит цикл, т.е. повторяющуюся группу команд, то в алгоритме должно присутствовать некое условие, при выполнении которого следует прерывание цикла.

Например, еще древние греки знали метод приближенного извлечения квадратного корня из произвольного числа а > 0. Пусть х⁽⁰⁾ – некоторое начальное приближение к 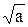. Для вычисления каждого следующего приближения построим рекуррентную формулу:

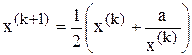, k = 0, 1, … (2.1)

называемую алгоритмом Герона.

Вычислим с его помощью 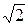, взяв х⁽⁰⁾ = 1.5. Последовательно получим х⁽¹⁾ = 1.4166667; х⁽²⁾ = 1.4142157; х⁽³⁾ = 1.4142136; х⁽⁴⁾ = 1.4142136. Теоретически эти вычисления можно продолжать бесконечно, получая все более точный результат, поэтому формула (2.1), строго говоря, алгоритмом не является.

Для того, чтобы ее с полным правом можно было назвать алгоритмом, надо указать условие окончания вычислений. Например, можно таким условием считать совпадение определенного количества N цифр в двух последовательных значениях х^(k) и х^(k+1). Доказано, что в этом случае при использовании формулы (2.1) у всех последующих приближений первые N цифр будут такими же, как у х^(k+1). В приведенном примере у х⁽³⁾ и х⁽⁴⁾ совпали первые N = 8 цифр. Следовательно, ответ получен с точностью 10^–7, и если она нас устроит, то вычисления можно заканчивать.

2) Определенность – каждая команда алгоритма должна быть четкой, однозначной и не оставлять места для произвола.

Благодаря этому свойству выполнение алгоритма носит чисто механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

Например, не является алгоритмом такая инструкция: слегка подогрейте в маленькой кастрюле немного коньяку, добавьте специи по вкусу. Здесь слова “слегка”, “немного” и т.д. носят неопределенный характер, который каждый исполнитель может трактовать по-своему.

3) Эффективность – все операции, которые необходимо произвести в алгоритме, должны быть достаточно простыми, чтобы их в принципе можно было выполнить точно и за разумное время с помощью карандаша и бумаги. Например, нельзя считать простой операцией решение алгебраического уравнения 12-й степени. Поэтому, если в инструкции присутствует такая команда: найти решение уравнения х¹² + 5х¹¹ + 15х¹⁰ + 22х⁵ + 15258 = 0, то такая инструкция эффективной не является, а, следовательно, ее нельзя считать алгоритмом.

4) Результативность – любой алгоритм должен после своей работы выдавать какой-нибудь результат.

Возможна ситуация, что поставленная задача вообще не имеет решения. В этом случае алгоритм должен заканчиваться выдачей сообщения: “нет решения”.

5) Массовость – алгоритм решения задачи разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

2.2. Формы записи алгоритма

На практике наиболее распространены следующие формы представления алгоритмов:

· словесная – запись на естественном (“человеческом”) языке;

· графическая – изображение команд в виде графических символов;

· программная – текст на языке программирования.

Словесный способ записи алгоритмов. Это <TBODY>описание последовательных этапов (шагов) обработки данных. Алгоритм задается в произвольном изложении на естественном языке. </TBODY>

Пример 2.1. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел.

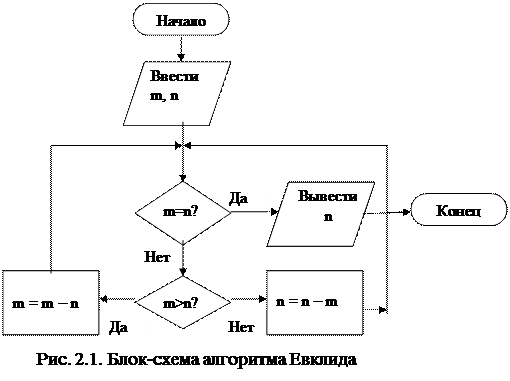
Предлагается следующий алгоритм – алгоритм Евклида.

1. Задать два числа.

2. Если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма.

3. Заменить большее из чисел разностью большего и меньшего из чисел.

4. Повторить алгоритм с шага 2.

Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедитесь в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75:

1. m = 125, n = 75.

2. m > n, значит

3. новое m = 125 – 75 = 50, n = 75. Возврат к 2.

2. n > m, значит

3. новое n = 75 – 50 = 25, m = 50. Возврат к 2.

2. m > n, значит

3. новое m = 50 – 25 = 25, n = 25. Возврат к 2.

2. m = n. Значит ОТВЕТ = 25.

Словесный способ не имеет широкого распространения по следующим причинам:

· описания не формализованы (нет строгих правил);

· страдают многословностью записей;

· допускают неоднозначность толкования отдельных предписаний.

Графический способ записи алгоритмов. Графический способ представления алгоритмов является более наглядным по сравнению со словесным.

<TBODY>При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.</TBODY> Такое представление называется блок-схемой алгоритма.

Таблица 2.1.
<TBODY>Название символа	Обозначение и пример заполнения	Пояснение
Процесс		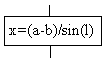Вычислительное действие или последовательность действий
Решение		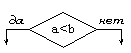Проверка условий
Модификация		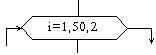Начало цикла
Ввод-вывод		Ввод-вывод в общем виде
Пуск-останов		Начало или конец алгоритма

В блок-схеме каждому типу действий соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий.

В таблице 2.1. приведены наиболее часто употребляемые символы.

Блок "процесс" применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения указанных данных. Для улучшения наглядности схемы несколько отдельных действий по обработке можно объединять в один блок. Представление отдельных операций достаточно свободно.

Блок "решение" используется для обозначения изменения порядка действий в зависимости от некоторого условия. В каждом блоке "решение" должны быть указаны вопрос, условие или сравнение, которые он определяет.

Блок "модификация" используется для организации циклических конструкций. Слово модификация означает видоизменение, преобразование. Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения. На рис. 2.1. приведена блок-схема алгоритма решения задачи примера 2.1.

Языки программирования. Это искусственные языки для записи компьютерных программ. В отличие от естественных языков, страдающих неоднозначностью, конструкция языков программирования такова, что составленные на них тексты обязательно обладают свойством определенности и эффективности – важными свойствами алгоритмов.

Запишем программу алгоритма решения задачи примера 2.1 на языке PASCAL.

var m, n: integer;

begin readln(m, n);

repeat if m = n then

begin writeln(n:5); halt; end;

if m > n then m:= m - n else n:= n - m;

until False;

Дата добавления: 2014-01-04