Общее решение для мод

Не рассматривая какую-либо конкретную физическую систему, предположим, что мы нашли два связанных линейных уравнения первого порядка не в нормальных координатах:

(1.6.5)

Рассмотрим колебание, соответствующее одной моде. Это значит, что обеим степеням свободы х и у соответствует гармоническое колебательное движение, совершаемое с одной и той же частотой и фазой. Таким образом, ,

где ω и B/A пока неизвестны. Имеем:

(1.6.6)

Подставляя (1.6.6) в (1.6.5), после элементарных преобразований получим два однородных линейных уравнения:

(1.6.7)

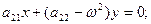(1.6.8)

или Ясно, что должно выполняться условие: Тогда

Левая часть этого уравнения представляет собой определитель, составленный из коэффициентов линейных однородных уравнений (1.6.7) и (1.6.8):

. (1.6.9)

Уравнение (1.6.9) является квадратным относительно 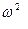. Оно имеет два решения и .

Итак, мы нашли, что существуют два способа, которыми могут быть реализованы колебания с единственной модой.

Частота 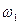соответствует моде 1, а – моде 2. Геометрическую конфигурацию, или форму моды 1 получим, подставив в уравнение (1.6.9) =: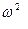

(1.6.10)

После того, как найдены частоты мод 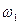и и отношения амплитуд B 1/ A 1 и B 2/ A 2, можно записать общие выражения суперпозиции двух мод:

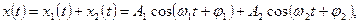(1.6.11)

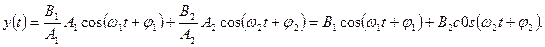(1.6.12)

Выбор постоянных 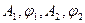в уравнении (1.6.11) накладывает ограничения на возможные значения постоянных в уравнении (1.6.12), так как должны удовлетворяться уравнения (1.6.10). Наиболее общее решение уравнений (1.6.5) состоит в комбинации двух независимых решений, которые удовлетворяют четырём начальным условиям для х (0); х'(0); у (0) и у '(0). Суперпозиция двух нормальных мод, для которых четыре константы 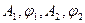определяются из четырёх начальных условий, представляют собой такое решение. Таким образом, общее решение может быть записано как суперпозиция мод.

Дата добавления: 2014-01-04