Эффект Доплера

Рассмотрим волну, распространяющуюся в упругой среде. На некотором расстоянии от источника волны располагается устройство, воспринимающее колебания (приемник). Если источник и приемник неподвижны относительно среды, в которой распространяется волна, то частота колебаний, воспринимаемых источником, будет равна частоте 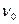колебаний источника. Если же источник или приемник (либо оба) движутся относительно среды, то частота 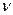, воспринимаемая приемником, отличается от 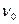. Это явление называется эффектом Доплера.

Будем считать, что приемник и источник движутся вдоль соединяющей их прямой. Скорость источника 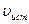будем считать положительной, если источник движется по направлению к приемнику, и отрицательной, если источник удаляется от приемника. Аналогично скорость приемника будем считать положительной, если приемник приближается к источнику, и отрицательной, если удаляется от него.

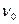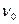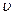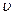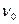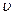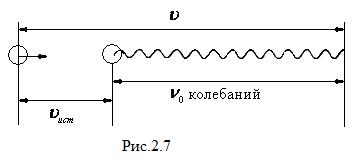
Если источник неподвижен и колеблется с частотой , то к моменту, когда источник будет завершать -е колебание, порожденный первым колебанием гребень волны успеет пройти в среде путь (- скорость распространения волны относительно среды). Следовательно, порожденные волной за секунду гребней и впадин волны уложатся по длине . Если же источник движется относительно среды со скоростью 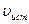, то в момент, когда источник будет завершать 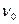-е колебание, гребень, порожденный первым колебанием, будет находиться от источника на расстоянии 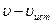(рис. 2.7). Следовательно, 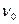гребней и впадин волны уложатся на длине 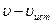, так что длина волны будет равна

.

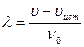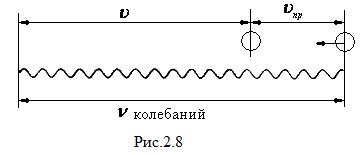
Мимо неподвижного источника пройдут за секунду гребни и впадины, укладывающиеся по длине 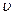. Если приемник движется со скоростью , то в конце секундного промежутка времени он будет воспринимать впадину, которая в начале этого промежутка отстояла от его теперешнего положения на 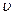. Таким образом, приемник воспринимает за секунду колебания, отвечающие гребням и впадинам, укладывающимся на длине 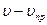(рис.2.8) и будет колебаться с частотой

.

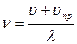Подставив 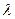из полученного ранее выражения, получаем

.

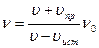Если расстояние между источником и приемником сокращается, воспринимаемая приемником частота оказывается больше частоты источника 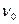. Если расстояние между источником и приемником растет, воспринимаемая частота будет меньше .

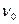Лекция 8

2 .10. Электромагнитные волны

2.10.1. Волновые уравнения для электромагнитного поля. Плоские и сферические электромагнитные волны. Волновой вектор. Волновое уравнение для электромагнитного поля. Основные свойства электромагнитных волн

Итак, переменное электрическое поле порождает переменное магнитное поле. Это переменное магнитное поле порождает электрическое и т.д. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникает последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс является периодическим в пространстве и во времени и представляет собой волну. Найдём уравнение этой волны.

В случае однородной нейтральной непроводящей среды с постоянными проницаемостями ε и μ имеем:

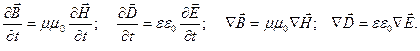
Поэтому уравнения Максвелла можно записать в виде:

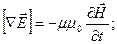(2.20)

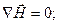(2.21)

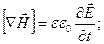(2.22)

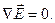(2.23)

Возьмём ротор от обеих частей уравнения (2.20):

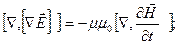
Изменим порядок дифференцирования по координатам (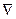) и времени (dt), получим:

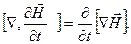
Подставив выражение (2.22), получим 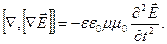Известно, что 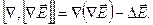Однако 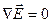, поэтому 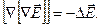Тогда: 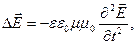или

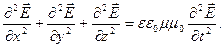(2.24)

Взяв ротор от обеих частей уравнения (2.22) и произведя аналогичные преобразования, получим:

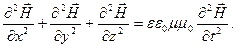(2.25)

(2.24)и (2.25)– это типичные волновые уравнения. Они описывают электромагнитную волну, фазовая скорость которой 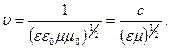В вакууме μ =1, ε =1, и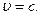

Рассмотрим плоскую электромагнитную волну, распространяющуюся в нейтральной непроводящей среде с постоянными проницаемостями ε и μ (ρ =0, 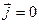, ε =const, μ =const). Направим ось Х перпендикулярно к волновым поверхностям. Тогда 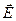и 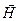не будут зависеть от координаты х, а будут зависеть только от координат y и z. Поэтому уравнения Максвелла (2.20) - (2.25) можно упростить и представить в виде:

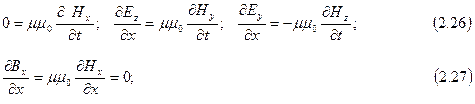
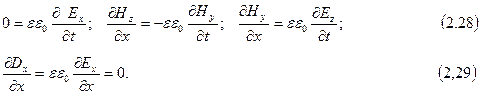
Уравнения (2.29) и (2.28) показывают, что Еx не зависит ни от х, ни от t. Уравнения (2.27) и (2.26) дают такой же результат для Нх. Следовательно, отличные от нуля Ех и Нх могут быть обусловлены лишь постоянными однородными полями, накладывающимися на электромагнитное поле волны. Само поле волны не имеет составляющих вдоль оси Х. Отсюда следует, что векторы 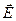и 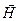перпендикулярны к направлению распространения волны, то есть электромагнитные волны поперечны.

Два последних уравнения (2.26) и (2.28) можно объединить в две независимые группы:

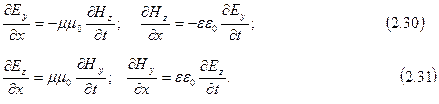
Первая группа уравнений связывает компоненты Ey и Hz, вторая – компоненты E zи Hy. Допустим, что первоначально было создано переменное электрическое поле Еу, направленное вдоль оси У. Согласно второму из уравнений (2.30) это поле создаёт магнитное поле Нz, направленное вдоль оси Z. В соответствии с первым уравнением (2.30) поле Нz создаёт электрическое поле Еу, и т.д. Ни поле Еz, ни поле Ну при этом не возникают. Аналогично, если первоначально было создано поле Еz, то согласно уравнениям (2.31) появится поле Ну, которое возбудит поле Еz, и т.д. В этом случае не возникают поля Еу и Нz. Таким образом, для описания плоской электромагнитной волны достаточно взять одну из систем уравнений (2.30) или (2.31), положив компоненты, фигурирующие в другой системе, равными нулю.

Возьмём для описания волны уравнение (2.30), положив 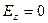, 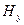=0. Продифференцируем первое уравнение по х и произведём замену:

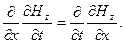
Подставим ∂ Hz/∂x из второго уравнения, получим волновые уравнения для Еу:

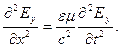(2.32)

Здесь заменили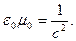

Продифференцируем по х второе уравнение из (2.30), найдём после аналогичных преобразований волновое уравнение для Hz:

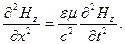(2.33)

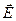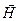Полученные уравнения представляют собой частные случаи уравнений (2.23) и (2.24). Так как Ex=Ez =0 и Hx=Hy =0, то Ey=E; Hz=H. Индексы у и z при E и H мы сохранили, чтобы подчеркнуть, что и перпендикулярны.

Простейшим решением уравнений (2.32) и (2.33) является:

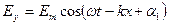, (2.34)

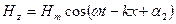, (2.35)

где ω – частота волн, 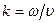– волновое число, 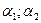– начальные фазы колебаний в точке х =0.

Подставим (2.34) и (2.35) в (2.30):

.

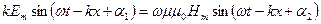
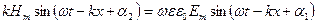Для удовлетворения этих уравнений необходимо, чтобы 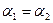, кроме того, должны выполняться соотношения:

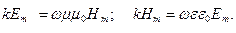
Перемножим два последних равенства: 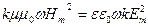, или .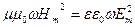

Таким образом, колебания электрического и магнитного векторов в электромагнитной волне происходят в одной фазе 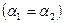, а амплитуды этих векторов связаны соотношением:

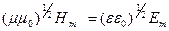
Для волны, распространяющейся в вакууме 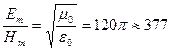Ом.

В векторной форме (2.34) и (2.35) примут вид :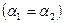

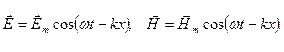
Векторы 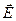и 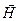образуют с направлением распространения волны правовинтовую систему.

Дата добавления: 2014-01-04