Свободные незатухающие гармонические колебания

Эти колебания возникают, если на систему массой m действует упругая сила

(5.1)

II закон Ньютона в этом случае запишется так:

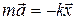. (5.2)

Пример: пружинный маятник. При сжатии одной из пружин маятник будет совершать колебания около положения равновесия (точка ). Проекция уравнения II закона Ньютона на ось :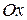

, (5.3)

Обозначим и (5.4)

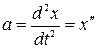. (5.5)

Тогда 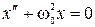(5.6)

- дифференциальное уравнение свободных незатухающих колебаний.

Решения этого уравнения имеют вид:

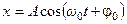или 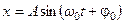, (5.7)

где 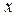- смещение от положения равновесия в момент времени ;

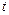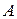- амплитуда колебаний, т.е. максимальное положительное смещение от положения равновесия;

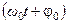- фаза колебаний, т.е. параметр, определяющий смещение от положения равновесия в данный момент времени;

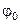- начальная фаза колебаний;

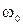- циклическая частота колебаний, численно равная числу полных колебаний за 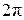секунд.

Для описания колебаний применяют также следующие величины:

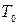- период колебаний, т.е. минимальный промежуток времени, через который фаза колебаний принимает одинаковые значения;

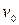- частота колебаний, численно равная числу колебаний за 1 секунду.

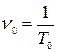, (5.8)

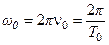. (5.9)

Зависимости физических величин от времени, которые описываются законом синуса или косинуса, называются гармоническими. Поскольку смещение от положения равновесия при свободных незатухающих колебаниях описывается законом синуса или косинуса, эти колебания называют также гармоническими.

При гармонических колебаниях не только смещение, но и скорость, и ускорение меняются с течением времени по гармоническому закону:

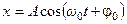, (5.10)

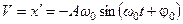, (5.11)

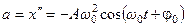. (5.12)

Графики этих зависимостей в пределах периода при представлены на рис. 5.1.

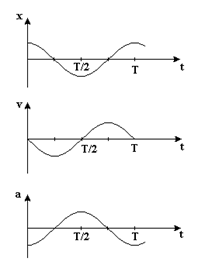
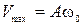
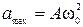
Рис.5.1

В каждый момент времени система, совершающая гармонические колебания, обладает и кинетической, и потенциальной энергией:

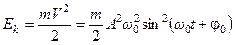, (5.13)

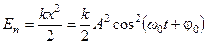. (5.14)

Полная энергия 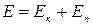, (5.15)

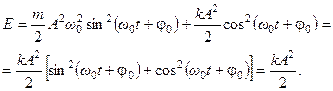(5.16)

Поскольку на систему действует только консервативная (упругая) сила, то полная механическая энергия остается постоянной (рис.5.2).

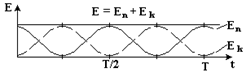
Рис. 5.2

Дата добавления: 2014-01-04