Тема 1. Предмет и система курса, история становления и развития коммерческого права

Контрольные задания

5.1. Незатухающие механические и электромагнитные колебания.

Сложение колебаний

1.1. Ниже под номерами 1, 2, 4 приведены графики зависимости волной W и потенциальной W_n энергии материальной точки от смещения x, а под номером 8 – график зависимости максимальной кинетической энергии W_{к max} от времени t для материальной точки.

Какие графики могут соответствовать незатухающим гармоническим колебаниям материальной точки? Укажите сумму их номеров.

1.2 Материальная точка совершает незатухающие гармонические колебания вдоль оси Ox. Для нее в произвольный момент времени t считаются, известными следующие величины:

1. x - смещение (координата), ()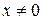

2. V_x - проекция скорости на ось,

4. F - модуль результирующей силы, действующей на точку,

8. W_к - кинетическая энергия.

Выразите угловую частоту 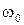колебаний точки через приведенные выше величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.

1.3 Уравнение колебаний материальной точки массой г имеет вид см.

Найти максимальную силу, действующую на точку F_max, и полную энергию W колеблющейся точки.

1.4 На рис. под номерами 1, 2 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных гармонических колебаний, а под номерами 4, 8 - векторные диаграммы сложения гармонических колебаний одного направления и одинаковой частоты (- векторы амплитуд складываемых колебаний; - вектор амплитуды результирующего колебания).

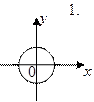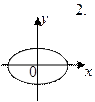а) для каких случаев разность 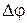фаз складываемых колебаний равна ? Укажите сумму их номеров.

б) для каких случаев амплитуды 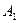и складываемых колебаний одинаковы? Укажите сумму их номеров.

1.5 Напряжение на конденсаторе в колебательном контуре (R =0) меняется по закону 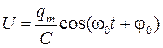, где

1. – амплитуда заряда на обкладках конденсатора;

2. C – емкость конденсатора;

4. 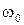– собственная частота колебаний;

8. 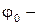начальная фаза колебаний.

Укажите сумму номеров величин, с помощью которых можно определить амплитуду илы тока в контуре.

1.6. В колебательном контуре заряд конденсатора изменяется по закону 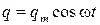, где мКл, рад/с. Чему равна энергия 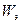электрического поля конденсатора в момент времени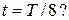 – период колебаний. Индуктивность контура мГн. Сопротивлением контура пренебречь.

Незатухающие механические и электромагнитные колебания.

Сложение колебаний

2.1 Ниже приведены графики зависимости смещения, скорости, потенциальной и кинетической энергии материальной точки, начинающей совершать гармонические колебания в момент времени t = 0. Обозначение вертикальных осей не указано.

Какой график соответствует смещению материальной точки? Какой график соответствует кинетической энергии материальной точки? Укажите сумму их номеров.

2.2. Для незатухающих гармонических колебаний пружинного маятника известны следующие величины:

1. W _к – кинетическая энергия маятника в момент времени t (W_к ≠ 0),

2. W _п – его потенциальная энергия в этот же момент времени,

4. k – жесткость пружины,

8. ω₀ – угловая частота колебаний маятника.

Выразите модуль F упругой силы, действующей на маятник в момент времени t, через приведенные выше величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.

2.3. Максимальная скорость точки, совершающей гармонические колебания, равна = 10 см/с, максимальное ускорение 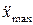= 100 см/с². Найти циклическую частоту ω колебаний, их период T и амплитуду A. Написать уравнение колебаний, приняв начальную фазу равной нулю.

2.4. Материальная точка участвует в двух взаимно перпендикулярных колебаниях. Траектория ее результирующего движения – окружность радиуса R =0,08 м. Определите амплитуды A ₁ и A ₂ и разность фаз Δφ складываемых колебаний. Предположим, что эти же два колебания будут происходить вдоль одного направления с теми же амплитудами A₁, A₂ и той же разностью фаз Δφ. Определить амплитуду A _p получаемого при этом результирующего колебания.

2.5. Известны уравнения незатухающих колебаний в двух контурах с разными индуктивностями и одинаковыми емкостями. В каком случае индуктивность контура меньше и во сколько раз?

1. q = 4cos(200π t + π), мкКл. q = 6cos400π t, мкКл.

2.6. В колебательном контуре с индуктивностью L = 10^-3 Гн происходят свободные гармонические колебания. При этом максимальное значение силы тока и заряда на обкладках конденсатора соответственно равны I_m = 1 А,

q_m = 10^-6 Кл. Какова емкость C этого контура?

Незатухающие механические и электромагнитные колебания.

Сложение колебаний

3.1. Ниже под номерами 2, 4, 8 приведены графики зависимости от смещения x полной W и потенциальной W_п энергии материальной точки, а под номером 1 – модуля F результирующей силы 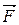, действующей на материальную точку.

Какие графики соответствуют гармоническим колебаниям материальной точки? Укажите сумму их номеров.

3.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси Ox. Для нее считаются известными следующие величины:

1. x – смещение точки в произвольный момент времени t (x ≠ 0);

2. a_x – проекция на ось Ox ускорения точки в этот же момент времени;

4. W – полная механическая энергия точки;

8. k – жесткость системы.

Выразите массу m материальной точки через эти величины. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.

3.3. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия x ₁ = 2,4 см скорость точки равна = 3 см/с, а при смещении x ₂ = 2,8 см скорость равна = 2 см/с. Найти амплитуду A и период T этого колебания.

3.4. Ниже под номерами 4, 8, 16 изображены траектории результирующего движения при сложении двух взаимно перпендикулярных колебаний, а под номерами 1, 2 – векторные диаграммы сложения гармонических колебаний одного направления и одинаковой частоты (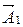, – векторы амплитуд складываемых колебаний; – вектор амплитуды результирующего колебания).

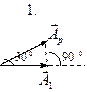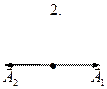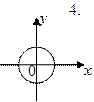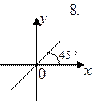а) для каких случаев разность фаз Δφ складываемых колебаний равна ? Укажите сумму их номеров;

б) для каких случаев амплитуды A ₁ и A ₂ складываемых колебаний не равны друг другу? Укажите сумму их номеров.

3.5. Колебательный контур состоит из катушки индуктивностью L = 10 мкГн и конденсатора емкостью C = 1 нФ. Максимальное напряжение U_m на обкладках конденсатора равно 100 В. Пользуясь приведенными данными, запишите уравнение изменения заряда на обкладках конденсатора в зависимости от времени. Сопротивлением контура пренебречь.

3.6. Максимальное напряжение на конденсаторе колебательного контура U_m = 80 В. Определить максимальную энергию W _{эл max} электрического поля конденсатора, если индуктивность контура L = 10^-2 Гн, период колебаний T =2π·10^-3 с. Сопротивлением контура пренебречь.

Незатухающие механические и электромагнитные колебания.

Сложение колебаний

4.1. Ниже приведены графики зависимости смещения, скорости, потенциальной и кинетической энергии материальной точки, начинающей совершать гармонические колебания в момент времени t = 0. Обозначение вертикальных осей не указано.

Какой график соответствует скорости материальной точки? Какой график соответствует потенциальной энергии материальной точки? Укажите сумму их номеров.

4.2. Материальная точка совершает незатухающие гармонические колебания вдоль оси Ox. Для нее в произвольный момент времени t считаются известными следующие величины:

1. V_x – проекция скорости на ось Ox (в момент t: V_x ≠ 0),
2. x – смещение (координата),
4. F – модуль результирующей силы, действующей на точку,
8. W_к – кинетическая энергия точки.

Через какие из этих величин можно выразить потенциальную энергию W_п точки в момент времени t? Укажите сумму их номеров.

4.3. Точка совершает гармоническое колебание. Период колебаний T = 2 с, амплитуда A = 50 мм, начальная фаза φ₀ = 0. Найти скорость 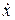точки в момент времени t, когда смещение x точки от положения равновесия равно 25 мм.

4.4. Два одинаково направленных гармонических колебания одного периода с амплитудами A ₁ = 4 см и A ₂ = 3 см складываются в одно колебание с амплитудой A _p = 5 см. Какова будет траектория результирующего движения, если эти же колебания будут происходить во взаимно перпендикулярных направлениях с теми же амплитудами и той же разностью фаз?

1. Эллипс. 2. Прямая линия. 4. Окружность. 8. Сложная фигура.

Для определения разности фаз складываемых колебаний используйте формулу для амплитуды результирующего колебания, полученного при сложении двух колебаний одинакового направления и частоты.

4.5. Известны уравнения изменения разности потенциалов на обкладках конденсатора в идеальном колебательном контуре (R = 0) с разными емкостями, но одинаковыми индуктивностями. В каком случае емкость контура больше?

1. U = 30cos(10π t + ), В. 2. U = 40cos8π t, В.

4.6. В идеальном колебательном контуре заряд конденсатора изменяется по закону q = q_m cosω t, где q_m = 8 мКл, ω = 10⁵ рад/с. Чему равна энергия W_m магнитного поля этого контура в момент времени t = ? T – период колебаний в контуре. Индуктивность контура L = 1 мГн.

5.2. Затухающие и вынужденные колебания

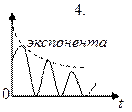1.1. Ниже приведены графики зависимости амплитуды, и энергии от времени t при различных видах механических колебаний, происходящих в замкнутых системах. Обозначение вертикальных осей не указано (β – коэффициент затухания колебаний).

.

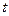Какой график может соответствовать зависимости амплитуды колебаний от времени, если колебания происходят в неконсервативной системе?

1.2. Уравнение затухающих колебаний материальной точки имеет вид

x = A₀e^{- β t} cos(ω t + φ₀),

где A ₀ = 0,01 м, β = 6 с^-1, φ₀ = .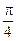

Чему равна частота ω затухающих колебаний, если логарифмический декремент затухания колебаний λ = 0,001?

1.3. Период затухающих колебаний в колебательном контуре равен T = 4·10^-5 с. При каком логарифмическом декременте затухания λ амплитуда U_m напряжения на конденсаторе за время t = 10^-3 с уменьшится в e раз (e – основание натурального логарифма)?

1.4. Ниже приведены уравнения затухающих электромагнитных колебаний. В каком случае период собственных колебаний колебательного контура наименьший?

1. q = q ₀ e ^{-β t} cosω t, q ₀ = 10^-8 Кл, β = 2 с^-1, ω = 2π рад/с.

2. q = q ₀ e^{- β t} cos(ω t + φ₀), q ₀=10^-4 Кл, β = 4 с^-1, ω=2π рад/с, φ₀ = .

4. U = U ₀ e^{- β t} cosω t, U ₀ = 10^-6 В, β = 1 с^-1, ω = 4π рад/с.

8. U = U ₀ e^{- β t} cos(ω t + φ₀), U ₀ = 10^-2 В, β = 3 с^-1, ω=4π рад/с, φ₀= .

1.5. Логарифмический декремент затухания колебаний маятника λ = 0,003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда колебаний уменьшилась в два раза?

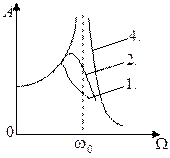1.6. На рисунке приведены графики зависимости амплитуды A вынужденных колебаний от частоты Ω вынуждающей силы для трех систем с различными значениями коэффициента затухания колебаний β и одинаковой частотой ω₀ собственных незатухающих колебаний.

Для какой системы логарифмический декремент затухания наибольший?

Затухающие и вынужденные колебания

2.1. Ниже приведены графики зависимости потенциальной W _п и максимальной кинетической W _{к max} энергий от времени t при различных видах механических колебаний. Обозначения вертикальных осей не указаны.

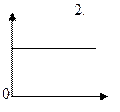
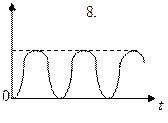
Какой график может соответствовать зависимости потенциальной W _п энергии системы от времени в случае колебаний, происходящих в неконсервативной системе?

2.2. Уравнение затухающих колебаний материальной точки имеет вид

x = A ₀ e^{- β t} cos(ω t + φ₀).

Во сколько раз уменьшится полная механическая энергия точки через время t = 10 с, если коэффициент затухания β = 0,1 с^-1?

2.3. Колебательный контур состоит из катушки с индуктивностью L = 2,5 мГн и конденсатора емкости C = 25 мкФ. При каком наименьшем значении сопротивления R _кр контура в нем будет наблюдаться апериодический разряд, т.е. ω= 0.

2.4. Ниже приведены уравнения затухающих электромагнитных колебаний. В каком случае логарифмический декремент затухания наибольший?

1. q = q ₀ e ^-βtcosω t, q ₀ = 10^-8 Кл, β = 1 с^-1, ω = 4π рад/с.

2. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-6 Кл, β = 1 с^-1, ω = 2π рад/с.

4. U = U ₀ e^{- β t} cosω t, U ₀ = 2 В, β = 4 с^-1, ω = π рад/с.

8. U = U ₀ e^{- β t} cos(ω t + φ₀), U ₀ = 5 В, β = 2 с^-1, ω=2π рад/с, φ₀=.

2.5. Чему равна длина математического маятника, если логарифмический коэффициент затухания l равен 0,01, а коэффициент затухания b=2 с^-1?

2.6. На рисунке приведены графики зависимости амплитуды A вынужденных колебаний от частоты Ω вынуждающей силы для четырех систем с различными значениями коэффициента затухания колебаний β и одинаковой частотой ω₀ собственных незатухающих колебаний.

В каком случае амплитуда F_m вынуждающей силы максимальна?

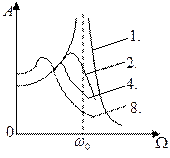Для какой системы коэффициент затухания β наименьший?

Укажите сумму номеров соответствующих графиков.

Затухающие и вынужденные колебания

3.1. Ниже приведены графики зависимости кинетической W_к и максимальной потенциальной W_{п max} энергий от времени t при различных видах механических колебаний. Обозначения вертикальных осей не указаны.

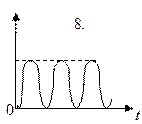Какой график может соответствовать зависимости максимальной потенциальной W _{п max} энергии системы от времени в случае затухающих колебаний?

3.2 Уравнение затухающих колебаний материальной точки имеет вид

x = A ₀ e^{- β t} cos(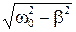 t + φ₀),

где A ₀ = 10 см, ω₀ = 10 рад/с.

Чему равен период T колебаний этой точки, если коэффициент затухания колебаний β = 8 с^-1?

3.3. Колебательный контур состоит из катушки индуктивностью L = 10 мГн, конденсатора емкостью C = 0,1 мкФ и резистора сопротивлением R = 20 Ом. Определите период колебаний T контура и логарифмический декремент затухания λ.

3.4. В каком случае время релаксации затухающих электромагнитных колебаний наибольшее?

1. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-8 Кл, β = 2 с^-1, ω = 4π рад/с.

2. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-6 Кл, β = 2 с^-1, ω = 6π рад/с.

3. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-6 В, β = 1 с^-1, ω = 2π рад/с.

4. q = q₀e^{- β t} cosω t, q ₀ = 10^-8 В, β = 3 с^-1, ω = 2π рад/с.

3.5. Через какое время амплитуда колебаний, совершаемых пружинным маятником, уменьшится в 3 раза, если период T незатухающих колебаний равен 4с, а логарифмический декремент затухания λ равен 0,5?

3.6. Два электрических колебательных контура имеют одинаковые частоты собственных незатухающих колебаний (ω₀₁ = ω₀₂ = ω₀). На рисунке приведены графики зависимости амплитуды напряжения U_m на конденсаторе от частоты Ω внешнего напряжения.

Какой контур обладает большей индуктивностью, если R ₁ = R ₂?

Затухающие и вынужденные колебания

4.1. Ниже приведены графики зависимости амплитуды и энергии от времени t при различных видах механических колебаний, происходящих в замкнутых системах. Обозначение вертикальных осей не указано (β – коэффициент затухания колебаний).

Какой график может соответствовать полной энергии затухающих колебаний?

4.2. Уравнение затухающих колебаний имеет вид

x = A ₀ e^{- β t} cos(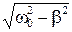t+ φ₀),

где A ₀ = 1 см, ω₀ = 10 рад/с.

Чему равен логарифмический декремент затухания колебаний λ, если β=8с^-1?

4.3. Колебательный контур имеет емкость C = 10^-9 Ф и индуктивность L =4·мГн. Логарифмический декремент затухания λ = 0,005. За какое время t вследствие затухания потеряется 75% энергии контура? Считать, что частота колебаний ω в контуре равна частоте ω₀ незатухающих колебаний.

4.4. Ниже приведены уравнения затухающих электромагнитных колебаний. В каком случае время релаксации наибольшее?

1. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-8 Кл, β = 2 с^-1, ω = 4π рад/с.

2. q = q ₀ e^{- β t} cosω t, q ₀ = 10^-6 Кл, β = 1 с^-1, ω = 2π рад/с.

4. U = U ₀ e^{- β t} cosω t, U ₀ = 2 В, β = 4 с^-1, ω = π рад/с.

8. U = U ₀ e^{- β t} cos(ωt + φ₀), U ₀ = 5 В, β = 2 с^-1, ω=2π рад/с, φ₀=.

4.5. Гиря массой m = 500 г подвешена к спиральной пружине и совершает упругие колебания в некоторой среде. Амплитуда колебаний уменьшилась в n = 2 раза за N = 99 полных колебаний маятника. Определить жесткость k пружины маятника.

4.6. Частица совершает вынужденные колебания под действием внешней вынуждающей силы. Коэффициент затухания колебаний частицы β.

На рисунке под номером 1 приведен график зависимости амплитуды A колебаний от частоты Ω вынуждающей силы.

Какой из трех других графиков будет соответствовать зависимости A (Ω), если коэффициент затухания колебаний β уменьшится?

5.3. Волны

1.1. В упругой среде распространяется плоская монохроматическая продольная волна. Ниже стрелками указаны направления колебаний частиц среды.

В каких случаях вектор скорости волны может лежать в плоскости xOy? Укажите сумму номеров этих диаграмм.

1.2. В упругой среде распространяется механическая волна от источника, начинающего совершать незатухающие гармонические колебания в момент времени t = 0.

Известны следующие величины:

1. Δ x – расстояние между выделенной частицей среды и источником колебаний,

2. t ₀ – момент начала колебаний этой частицы,

4. A – амплитуда волны,

8. λ – длина волны.

С помощью приведенных выше величин получите формулу для разности фаз Δφ колебаний выделенной частицы среды и источника колебаний. Какие из них вошли в расчетную формулу? Укажите сумму их номеров.

1.3. Найти смещение ξ от положения равновесия точки, отстоящей от источника колебаний на l = 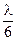, для момента t = 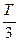, если амплитуда колебаний A = 10 см.

x(x)  

1.4. На рисунке приведены графики смещения частиц среды в стоячей волне для двух различных моментов времени.

Чему равна (в СИ) разность фаз Δφ колебаний частиц с координатами x ₁ и x ₂?

1.5. В среде с магнитной проницаемостью μ = 1 и диэлектрической проницаемостью ε = 9 в положительном направлении оси Oy распространяется плоская электромагнитная волна.

На рисунке приведен график зависимости от времени проекции E_z на ось Oz напряженности электрического поля волны в произвольной точке оси Oy. Определите длину волны λ в среде.

1.6. Определите амплитуду вектора Пойнтинга этой волны.

Волны

2.1. В упругой среде распространяется плоская монохроматическая волна. В начальный момент времени t = 0 все частицы среды находились в покое. На рис. приведен график зависимости от времени смещения ξ частицы, отстоящей от источника колебаний на расстоянии x = 2 м. Чему равна длина волны λ?

2.2. Чему равна (в СИ) разность фаз Δφ колебаний частиц среды, отстоящих от источника колебаний на расстояниях x ₁ = 2 м и x₂ = 4 м?

2.3. Уравнение незатухающих колебаний дано в виде ξ = 10sin0,5wt, см.

1). Написать уравнение волны, если скорость распространения колебаний = 300 м/с. 2). Написать уравнение колебаний для точки, отстоящей на расстоянии l = 600 м от источника колебаний.

2.4. В упругой среде возникла стоячая волна. Верно ли, что…

1. … амплитуда колебаний всех частиц одинакова?

2. … расстояние между соседними пучностями равно ?

4. … все частицы среды одновременно проходят положение равновесия?

8. … все частицы среды колеблются в одинаковой фазе?

На какие вопросы Вы ответили «да»? Укажите сумму их номеров?

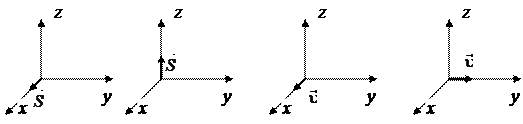2.5. Ниже стрелками указаны векторы скорости и векторы Умова-Пойнтинга плоской электромагнитной волны

.

В каких случаях плоскость векторов и 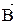совпадает с плоскостью xOy? Укажите сумму номеров этих диаграмм.

2.6. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волны и характеристики среды:

1. ε – диэлектрическая проницаемость среды,

2. ω_м – плотность энергии магнитного поля волны,

4. – скорость волны,

8. ω – угловая частота волны.

Получите выражение для модуля вектора магнитной индукции B волны только через приведенные выше величины и константы ε₀, μ₀, c. Укажите сумму номеров величин, вошедших в расчетную формулу.

Волны

3.1. На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t =4 с. Источник колебаний находится в точке с координатой x = 0. В начальный момент времени (t =0) все частицы среды находились в покое. Чему равна скорость распространения волны?

3.2. В упругой среде распространяется механическая волна от источника, начинающего совершать незатухающие гармонические колебания в момент времени t = 0. Считаются известными следующие величины:

1. Δ x – расстояние между точкой среды и источником колебаний,

2. t ₀ – момент начала колебаний этой частицы,

4. T – период волны,

8. A – амплитуда волны.

Через эти величины выразите длину волны λ. Укажите сумму номеров величин, вошедших в расчетную формулу.

3.3. Определить скорость распространения волны в упругой среде, если разность фаз Δφ двух точек среды, отстоящих друг от друга на расстоянии Δ x =10 см, равна 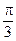. Частота колебаний равна ν = 25 Гц.

3.4. На рисунке приведен график модуля амплитуды стоячей волны от координаты x.

Чему равны амплитуды A бегущей и отраженной волн, при наложении которых была получена эта стоячая волна? Определить длину бегущей волны.

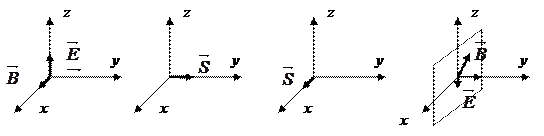3.5. Ниже под номерами 1, 8 указаны векторы напряженности электрического и индукции магнитного полей, а под номерами 2, 4 – векторы Умова-Пойнтинга плоской электромагнитной волны.

В каких случаях электромагнитная волна распространяется в положительном направлении оси Oy? Укажите сумму номеров соответствующих диаграмм.

3.6. В среде с магнитной проницаемостью μ = 1 и диэлектрической проницаемостью ε = 9 в положительном направлении оси Oy распространяется плоская электромагнитная волна.

На рис. приведен график зависимости проекции B_x на ось Ox индукции магнитного поля волны от координаты y в произвольный момент времени t.

Определите период T волны.

Волны

4.1. В упругой среде распространяется плоская монохроматическая волна. Ниже под номерами 1, 2 изображены направления вектора скорости поперечной волны, а под номерами 4, 8 – направления вектора скорости продольной волны.

В каких случаях колебания частиц среды могут происходить вдоль оси Oy? Укажите сумму номеров этих диаграмм.

0,01

4.2. В упругой среде распространяется плоская монохроматическая волна. На рисунке приведены моментальные «фотографии» волны в моменты времени t ₁ и t ₂, причем t ₂ - t ₁= 1 с. Чему равна максимальная скорость колебания частицы среды?

Чему равна скорость распространения волны?

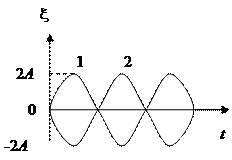
4.3. Найти смещение от положения равновесия точки ξ, отстоящей от источника колебаний на l = , для момента t = . Амплитуда колебаний A = 0,05 м.

4.4. Стоячая волна образовалась наложением бегущей и отраженной волн с длиной волны λ =14 м. На рисунке приведены графики смещения двух частиц среды в зависимости от времени. Чему равно минимальное расстояние Δ x между этими частицами?

4.5. В среде распространяется плоская электромагнитная волна. Известны следующие параметры волны и характеристики среды:

1. ε – диэлектрическая проницаемость среды,

2. μ – магнитная проницаемость среды,

4. ω – угловая частота волны,

8. E _м – амплитуда напряженности электрического поля волны.

Получите выражение для длины волны λ в среде через приведенные выше величины и константы ε₀, μ₀, c. Укажите сумму номеров величин, входящих в расчетную формулу.

4.6. Получите выражение для амплитудного значения S_m вектора Умова-Пойнтинга через приведенные выше величины и константы ε₀, μ₀, c. Какие из величин вошли в расчетную формулу? Укажите сумму номеров.

Оглавление

1. Список основных формул 3

2. Незатухающие механические и электромагнитные колебания. Сложение

колебаний. 8

2.1. Примеры решения задач 8

2.2. Задачи для самостоятельного решения 17

3. Затухающие механические и электромагнитные колебания 21

3.1. Примеры решения задач 21

3.2. Задачи для самостоятельного решения 30

4. Волны в упругой среде 33

4.1. Примеры решения задач 33

4.2. Задачи для самостоятельного решения 38

5. Контрольные задания 40

5.1. Незатухающие механические и электромагнитные колебания.

Сложение колебаний. 40

5.2. Затухающие механические и электромагнитные колебания 48

5.3. Волны 56

Физика:

Колебания и волны

Модуль№5

Рабочая тетрадь

Составители Ромашева Людмила Федоровна

Андреева Анна Григорьевна

Редактор Н.П. Кубыщенко

Подписано в печать 22.10.2004 Формат 60´84 1/16

Бумага типографская Офсетная печать Усл. печ. л. 2,91

Уч.-изд. л. 3,40 Тираж Заказ Цена ²С²

ООО ²Издательство УМЦ УПИ²

620002, Екатеринбург, Мира, 17

Понятие коммерции и коммерческого права. Коммерческое право как наука и как учебная дисциплина, предмет коммерческого права.

Источники коммерческого права.

История становления и развития коммерческого (торгового) права в мире.

История торгового законодательства в России.

Современное состояние российского торгового законодательства. Его место в системе права России. Перспективы развития.

Дата добавления: 2014-01-04