
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 11
|
|
|
|
ЭЛЕКТРОДИНАМИКА
Электрические колебания.
Процессы, происходящие в идеальном
колебательном контуре.
Электромагнитные колебания – это колебания величин заряда, силы тока, напряжения, эдс индукции и характеристик переменного электромагнитного поля.
 Электромагнитные колебания создаются в закрытом колебательном контуре, который представляет собой электрическую цепь, содержащую катушку индуктивности и конденсатор (рис. 11.1)
Электромагнитные колебания создаются в закрытом колебательном контуре, который представляет собой электрическую цепь, содержащую катушку индуктивности и конденсатор (рис. 11.1)
Свободных (собственные) колебания – это ко -
Рис.11.1 лебания, которые совершаются без внешнего воздействия за счет первоначально накопленной энергии.
Рассмотрим идеальный колебательный контур, в котором активное сопротивление 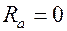 (рис.11.2).
(рис.11.2).
 Если переведем ключ в положение 1, то конденсатор зарядится от источника тока так, что на его пластинах накопится максималь-ный заряд
Если переведем ключ в положение 1, то конденсатор зарядится от источника тока так, что на его пластинах накопится максималь-ный заряд  . Перебросим ключ в положение 2 и рассмотрим процессы, происходящие в контуре, считая, что в момент включения
. Перебросим ключ в положение 2 и рассмотрим процессы, происходящие в контуре, считая, что в момент включения  .
.
Рис. 11.2
Процесс будем рассматривать в течение одного периода (рис.11.3).
1. При  мгновенное значение тока
мгновенное значение тока 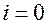 .
.
2. В промежуток времени от  до
до 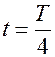 конденсатор начинает разряжаться, заряд будет уменьшаться, напряжение на обкладках конденсатора
конденсатор начинает разряжаться, заряд будет уменьшаться, напряжение на обкладках конденсатора 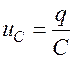 также будет уменьшаться. В контуре появится электрический ток
также будет уменьшаться. В контуре появится электрический ток  , который будет возрастать в этот промежуток времени. Проходя по катушке, возрастающий ток образует вокруг нее магнитное поле, которое будет возбуждать в катушке эдс самоиндукции. Эдс самоиндукции замедляет нарастание тока. Величина эдс определяется, как
, который будет возрастать в этот промежуток времени. Проходя по катушке, возрастающий ток образует вокруг нее магнитное поле, которое будет возбуждать в катушке эдс самоиндукции. Эдс самоиндукции замедляет нарастание тока. Величина эдс определяется, как  .
.
В момент времени 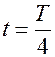 параметры контура:
параметры контура:  (конденсатор разрядился),
(конденсатор разрядился), 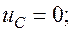

 3. В промежуток времени от
3. В промежуток времени от 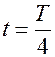 до
до 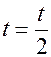 ток
ток 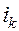 начинает убывать, в катушке возникает эдс индукции, замедляющая убывание тока. Под действием индукционного тока конденсатор перезаряжается – на пластинах появляется заряд противоположного знака.
начинает убывать, в катушке возникает эдс индукции, замедляющая убывание тока. Под действием индукционного тока конденсатор перезаряжается – на пластинах появляется заряд противоположного знака.
В момент времени
Рис. 11.3
 параметры контура:
параметры контура: 

4. В промежутки времени от  до
до 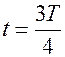 и от
и от 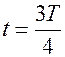 до
до  процесс повторяется в обратном направлении (рис. 11.3).
процесс повторяется в обратном направлении (рис. 11.3).
Таким образом, в колебательном контуре возникают электромагнитные колебания – колебания заряда, тока, напряжения и эдс индукции.
Незатухающие электромагнитные колебания.
Такие колебания происходят в идеальном колебательном контуре, в котором 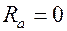 и не происходит потерь первоначально накопленной энергии на нагревание проводов. Согласно второму правилу Кирхгофа: сумма напряжений на элементах замкнутого контура равна сумме эдс, заключенных в этом контуре
и не происходит потерь первоначально накопленной энергии на нагревание проводов. Согласно второму правилу Кирхгофа: сумма напряжений на элементах замкнутого контура равна сумме эдс, заключенных в этом контуре
 .
.
Т.к. 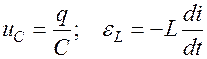 , то дифференциальное уравнение, описывающее незатухающие электрические колебания имеет вид:
, то дифференциальное уравнение, описывающее незатухающие электрические колебания имеет вид:
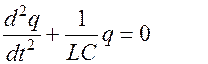
Его решением являются функции 
 .
.
График этой функции, а также графики напряжения, тока и эдс индукции представлены на рис.11.4:

Рис.11.4.
Напряжение на конденсаторе  сила тока
сила тока
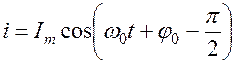 , Эдс индукции
, Эдс индукции  .
.
Период колебаний незатухающих колебаний определяется по формуле Томсона: 
Затухающие колебания
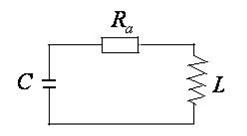 Рассмотрим свободные колебания в реальном колебательном контуре (рис.11.5). В нём
Рассмотрим свободные колебания в реальном колебательном контуре (рис.11.5). В нём 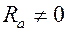 , следовательно, провода катушки будут нагреваться, энергия, первоначально накопленная энергия будет теряться. Такие колебания называются затухающими.
, следовательно, провода катушки будут нагреваться, энергия, первоначально накопленная энергия будет теряться. Такие колебания называются затухающими.
Рис.11.5
Согласно второму правилу Кирхгофа для данного контура
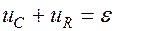

Дифференциальное уравнение для затухающих колебаний

где  и
и  (
(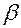 - коэффициент затухания).
- коэффициент затухания).
Его решением является функция
 или
или
 .
.
В этих уравнениях величина  амплитуда затухающего колебания. Знак минус в показателе степени говорит о том, что амплитуда убывает с течением времени по экспоненте. Само же колебание остаётся гармоническим. График затухающего колебания показан на рисунке (11.6):
амплитуда затухающего колебания. Знак минус в показателе степени говорит о том, что амплитуда убывает с течением времени по экспоненте. Само же колебание остаётся гармоническим. График затухающего колебания показан на рисунке (11.6):

Рис.11.6
Быстрота затухания колебаний характеризуется логарифмически декрементом затухания

Добротность 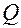 .
.
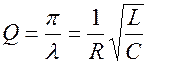 ,
,
Вынужденные колебания.
Чтобы колебания в контуре были не затухающими, к нему необходимо подать внешнюю эдс (рис.11.7), которая должна быть периодической и должна иметь частоту колебаний 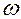 , отличную от частоты собственных колебаний:
, отличную от частоты собственных колебаний: 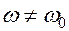 . Источник внешней эдс можно включать как параллельно, так и последовательно (рис.11.7).
. Источник внешней эдс можно включать как параллельно, так и последовательно (рис.11.7).
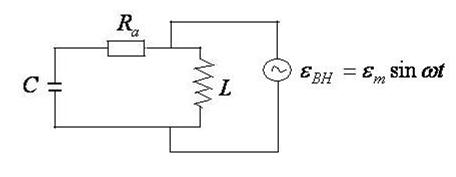
Рис.11.7
Второе правило Кирхгофа для такого контура запишется в виде
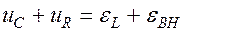

Дифференциальное уравнение вынужденных колебаний

Решением этого уравнения является функция
 или
или
 .
.
Колебания происходят с частотой внешней эдс. Начальная фаза колебаний меняется на новую фазу 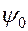 , Само же колебание остается гармоническим. Амплитуда вынужденных колебаний зависит от параметров источника внешней эдс
, Само же колебание остается гармоническим. Амплитуда вынужденных колебаний зависит от параметров источника внешней эдс
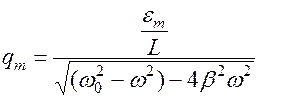
При малых затуханиях, т.е. при 
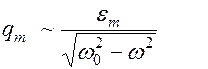
Если  , то происходит резкое возрастание амплитуды заряда на пластинах конденсатора и напряжения. Это явление называется резонансом.
, то происходит резкое возрастание амплитуды заряда на пластинах конденсатора и напряжения. Это явление называется резонансом.
Контрольные вопросы
•Идеальный колебательный контур. Процессы, происходящие в нем. •Свободные незатухающие колебания. Дифференциальное уравнение, описывающее их. Решение уравнения. Графики изменения заряда, силы тока, напряжения, ЭДС. Формула Томсона. •Реальный колебательный контур. Затухающие электромагнитные колебания. Дифференциальное уравнение, решение, график. Логарифмический декремент затухания, добротность. •Вынужденные электромагнитные колебания. Дифференциальное уравнение, решение. Резонанс. •Автоколебания. Генератор незатухающих электромагнитных колебаний на примере аппарата УВЧ-терапии.
Тема 12.
ИМПУЛЬСНЫЕ ТОКИ
Апериодический разряд конденсатора
 Если конденсатор подключить к источнику постоянного тока (рис. 12.1, а), то пластины конденсатора заряжаются разноименно и в диэлектрике между пластинами возникает электрическое поле. Во внешней цепи появляется кратковременный импульс – ток зарядки конденсатора.
Если конденсатор подключить к источнику постоянного тока (рис. 12.1, а), то пластины конденсатора заряжаются разноименно и в диэлектрике между пластинами возникает электрическое поле. Во внешней цепи появляется кратковременный импульс – ток зарядки конденсатора.
Если заряженный конденсатор отключить от источника напряжения и замкнуть его на сопротивление 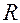 (рис.12.1 б), то разность потенциалов
(рис.12.1 б), то разность потенциалов 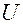 на его пластинах вызовет движение электронов во внешней цепи в направлении обратном первоначальному. В цепи образуется
на его пластинах вызовет движение электронов во внешней цепи в направлении обратном первоначальному. В цепи образуется
кратковременный импульс тока – ток разрядки конденсатора.
Рис.12.1
Мгновенные значения тока разрядки определяются по формуле
 .
.
Аналогично изменяется и напряжение на обкладках конденсатора. Графики тока разрядки и напряжения показаны на рис. 12.2
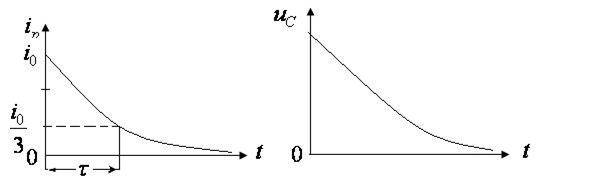
Рис.12.2
 За длительность импульса условно принимается время
За длительность импульса условно принимается время  , такое, что ток уменьшается за это время до величины
, такое, что ток уменьшается за это время до величины 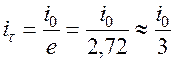 . Время
. Время  называется постоянной времени разрядки конденсатора.
называется постоянной времени разрядки конденсатора.

Рис.12.3
Ток зарядки имеет такую же форму, как и ток разрядки, но течет в противоположном направлении (рис.12.3).
Таким образом, импульсы – это кратковременные изменения силы тока и напряжения.
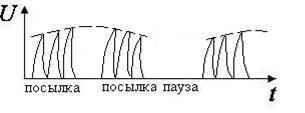
Импульсный ток – это повторяющиеся во времени импульсы. Они могут быть самой различной формы (рис. 12.4):

Рис. 12.4
Характеристики импульсных токов.
1. Длительность импульса - 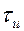 время, при котором напряжение (или сила тока) не меньше
время, при котором напряжение (или сила тока) не меньше 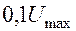 (рис.12.5)
(рис.12.5)

Рис. 12.5
2. Крутизна фронта характеризует скорость нарастания напряжения или силы тока
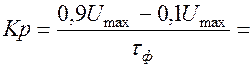
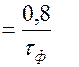
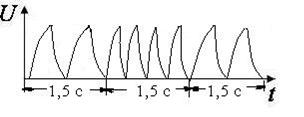
3. Период 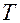 характеризует период повторения импульсов – это среднее время между началами двух соседних импульсов.
характеризует период повторения импульсов – это среднее время между началами двух соседних импульсов.
4. Частота повторения импульсов

5. Скважность следования импульсов
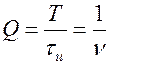
6. Коэффициент заполнения

Генераторы импульсных токов.
 1. Генератор на неоновой лампе представлен на рис.12.6.
1. Генератор на неоновой лампе представлен на рис.12.6.

Рис. 12.6 Рис. 12.7

Неоновая лампа зажигается при определенном напряжении 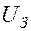 , а гаснет при меньшем напряжении
, а гаснет при меньшем напряжении  . График выходного напряжения приведен на рис.12.7. Меняя
. График выходного напряжения приведен на рис.12.7. Меняя 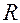 и
и 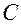 , можно так подобрать эти параметры, что напряжение будет пилообразным (рис.12.8):
, можно так подобрать эти параметры, что напряжение будет пилообразным (рис.12.8):
Рис. 12.8
3.  Блокинг-генератор. Схема его представлена на рис.12.9, (а). На рис. 12.9, б) условно показан график выходного напряжения.
Блокинг-генератор. Схема его представлена на рис.12.9, (а). На рис. 12.9, б) условно показан график выходного напряжения.
Рис. 12.9
3. Мультивибратор. Схема его представлена на рис.12.10
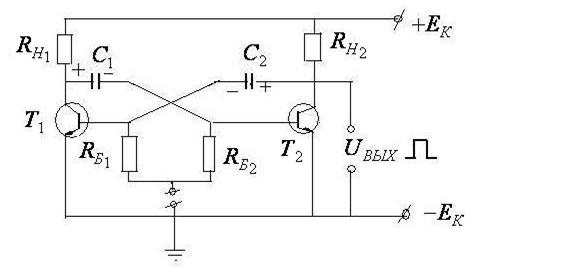
Рис.12.10
Мультивибратор содержит два транзистора, два конденсатора и по паре сопротивлений  и
и  .
.
Конденсаторы служат для генерации импульсов (заряжаются от источника постоянного тока  и сопротивления
и сопротивления  , а разряжаются через сопротивления
, а разряжаются через сопротивления  ). Транзисторы играют роль “включателей”. Симметричное их расположение в схеме обеспечивает поочередную зарядку конденсаторов: если открыт транзистор
). Транзисторы играют роль “включателей”. Симметричное их расположение в схеме обеспечивает поочередную зарядку конденсаторов: если открыт транзистор 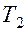 , то заряжается конденсатор
, то заряжается конденсатор  , если открыт транзистор
, если открыт транзистор  , то заряжается конденсатор
, то заряжается конденсатор  . Выходное напряжение
. Выходное напряжение  имеет прямоугольную форму.
имеет прямоугольную форму.
Изменение формы импульса.
После мультивибратора получаются импульсы прямоугольной формы. Но для лечения различных заболеваний используют импульсы различной формы. Чтобы изменить форму импульса, на выходе мультивибратора собирают дифференцирующую (рис. 12.11) или интегрирующую цепь (рис.12.13):
1. Дифференцирующая цепь
Её применяют в том случае, если  .
.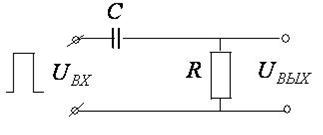
На вход цепочки подается входное напряжение прямоугольной формы. Очевидно,
| Рис. 12.11 |  . .
|
Выходное напряжение включено параллельно резистору 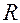 . Поэтому
. Поэтому
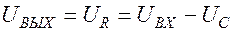

Форму выходного напряжения можно получить при графическом вычитании. На рис. 12.12 а) показан импульс входного напряжения. Затем импульс прекраща-ется, конденсатор разряжается (рис. 12.12 б). Вычитая значения функции, представленной на рис. 12.12 б) из значений функции, представленной на рис. 12.12 а), получаем вид функции выходного напряжения (рис. 12.12 в).
Рис. 12.12
Таким образом, на выходе из цепочки получаются два остроконечных импульса противоположного знака.
Рассмотренная цепочка называется дифференцирующей потому, что выходное напряжение пропорционально производной от входного напряжения 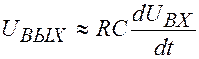 .
.
2. Интегрирующая цепь.
Применяется в том случае, если  .
.
 Выходное напряжение включено параллельно конденсатору
Выходное напряжение включено параллельно конденсатору 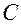 . Поэтому
. Поэтому
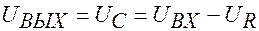 .
.
Рис.12.13
Если на вход цепи подан прямоугольный импульс (рис. 12.14 а), то напряжением на выходе является напряжение на пластинах конденсатора (рис.12.14 б). Конденсатор не успевает зарядиться до  .
.
 Рассмотренная цепочка называется интегрирующей потому, что выходное напряжение пропорционально интегралу
Рассмотренная цепочка называется интегрирующей потому, что выходное напряжение пропорционально интегралу 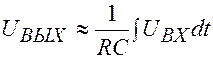 .
.
Действие импульсного тока на ткани организма
В основе действия электрического тока на ткани организма лежит движение заряженных частиц, преимущественно ионов тканевых электролитов, в результате чего изменяется обычный состав ионов по обе стороны мембраны, в связи, с чем в клетке происходит ряд биофизических и физиологических процессов, вызывающих её возбуждение. Рис. 12.14
Постоянный ток почти не оказывает раздражающего действия на ткани организма. Раздражение вызывается при изменении силы тока и зависит от скорости, с которой это изменение происходит. Это положение известно как закон Дюбуа-Реймона. Сила тока  в растворе электролита зависит как от числа движущихся ионов, так и от скорости их перемещения. Скорость изменения силы тока
в растворе электролита зависит как от числа движущихся ионов, так и от скорости их перемещения. Скорость изменения силы тока 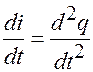 соответствует ускорению движения ионов.
соответствует ускорению движения ионов.
Очевидно, что раздражающее действие зависит от крутизны импульсов.
| Формы импульсных токов | Применение |
Прямоугольные:
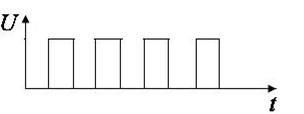
|  - электросон - электросон
 - электрокардиостимуляция - электрокардиостимуляция
|
Треугольные:

|  - возбуждение мышц, электрогимнастика - возбуждение мышц, электрогимнастика
|
Тетанизирующие:

|  Электростимуляция здоровых мышц Электростимуляция здоровых мышц
|
Экспоненциальные:

|
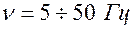 Электростимуляция
Электростимуляция
|
Экспоненциальные:
| Электростимуляция пораженных мышц |
Диадинамические:
| Электротерапия |
Рис. 12.15
Раздражающее действие прямоугольных импульсов в значительной мере зависит от их длительности 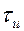 , обусловливающей наибольшее смещение ионов за время действия импульса. Эта зависимость описывается уравнением Вейса-Лапика
, обусловливающей наибольшее смещение ионов за время действия импульса. Эта зависимость описывается уравнением Вейса-Лапика

где  - пороговая сила тока (амплитуда импульса),
- пороговая сила тока (амплитуда импульса), 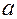 и
и 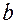 - коэффициенты, зависящие от природы возбуждаемой ткани и её функционального состояния. Зависимость
- коэффициенты, зависящие от природы возбуждаемой ткани и её функционального состояния. Зависимость  от
от 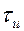 показана на рис. 12.16:
показана на рис. 12.16:
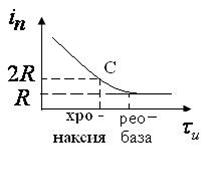 При достаточно длительных импульсах раздражающее действие становится независимым от длительности (
При достаточно длительных импульсах раздражающее действие становится независимым от длительности (
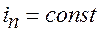 ). Значение порогового тока при этом называют реобазой
). Значение порогового тока при этом называют реобазой  . Точка
. Точка 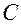 кривой, ордината которой равна удвоенной реобазе, определяет длительность импульса т называется хронаксией.
кривой, ордината которой равна удвоенной реобазе, определяет длительность импульса т называется хронаксией.
Рис. 12.16
Хронаксия и реобаза характеризуют возбудимость органа и могут служить показателями их функционального состояния или диагностического признака их поражения.
Контрольные вопросы
•Апериодический разряд конденсатора. Постоянная времени. •Принцип генерации импульсных токов на примере генератора с неоновой лампой и блокинг-генератора. Мультивибратор. •Электрический импульс и его характеристики. Импульсный ток. •Характеристики импульсных токов.•Изменение формы импульса (дифференцирующая и интегрирующая цепи).•Действие импульсных токов на организм. Закон Дюбуа-Реймона. Формула Вейса-Лапика. •Применение импульсных токов в медицине.
Тема 13.
ИМПЕДАНС ТКАНЕЙ ОРГАНИЗМА.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 728; Нарушение авторских прав?; Мы поможем в написании вашей работы!