
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Высокоточное нивелирование. Геодезические сети специального назначения (ГССН)
|
|
|
|
Геодезические сети специального назначения (ГССН)
Полевые работы на пунктах ГСС
Точные угловые измерения
Государственная геодезическая сеть (ГГС)
Фигура Земли и система координат
1.1. Понятие о фигуре Земли. Уровенные поверхности
1.2. Общеземной эллипсоид и референц-эллипсоид. Требования
1.3. Основные линии и плоскости земного эллипсоида. Нормальные сечения
1.4. Уклонения отвесных линий
1.5. Системы координат
1.6. Основные системы высот
2.1.1 ГГС. Сущность. Назначение. Виды
2.1.2 ГГС. Классификация. Понятие о плотности и точности
2.1.3 Астрономо-геодезическая сеть (АГС)
2.1.4 Геодезические сети сгущения 3-4 класса (ГСС)
2.1.5 Понятие об ориентирных пунктах ГГС
2.2. Методы создания геодезических сетей (Полигонометрия, Триангуляция, Трилатерация)
2.4. Закрепление пунктов ГГС на местности
2.5. Спутниковая геодезическая сеть [СГС] (ФАГС, ВГС, СГС-1)
2.6. Закрепление пунктов СГС
3.1. Точный оптический теодолит типа Т2 (3Т2КП)
3.2. Основные поверки точного оптического теодолита
3.3.1 Поверка цилиндрического уровня на алидаде ГК
3.3.2 Поверка установки сетки нитей
3.3.3 Поверка коллимационной ошибки
3.3.4 Поверка места зенита
3.3.5 Поверка положения оси вращения зрительной трубы
3.3.6 Поверка оптического центрира
3.3.7 Поверка оптического компенсатора
3.4.1 Исследования теодолита
3.4.2 Эксцентриситет лимба и алидады
3.4.3 Реон оптического микрометра
4.1. Основные источники ошибок
4.2. Способ измерения отдельного угла
4.3. Измерение зенитных расстояний
4.4. Способ круговых приемов
4.5.1 Поправки в направления за внецентренность теодолита
4.5.2 Поправка в длину линии за внецентренность
4.6.1 Определение элементов приведения. Графический способ
4.6.2 Определение высоты прибора и визирной цели над центром пункта
4.7. ОРП на пунктах ГГС
4.8. Производство и обработка линейных измерений
4.9. Первичные вычисления на пунктах ГГС
5.1.1 Общие сведения о ГССН
5.1.2 Полигонометрия ГССН
5.1.3. Закрепление пунктов ГССН на местности
5.2.1 Угловые измерения на пунктах полигонометрии ГССН
5.2.2 Линейные измерения в полигонометрии ГССН
5.2.3 Трехштативный метод
5.3.1 Передача координат на стенной знак. Линейная засечка
5.3.2 Передача координат на стенной знак. Угловая засечка
5.3.3 Передача координат на стенной знак. Полярный способ
5.3.4 Передача координат на стенной знак. Редуцирование
5.4.1 Привязка ГССН к опорным пунктам. Непосредственная привязка
5.4.2 Привязка ГССН к опорным пунктам. Привязка «снесением» координат
5.4.3 Привязка ГССН к опорным пунктам. Координатная привязка
6.1. Основные сведения о ГНС
6.2. Закрепление линий ГНС на местности
6.3.1 Высокоточные нивелиры
6.3.2 Поверки и исследования нивелира
6.4. Основная поверка нивелира
6.5.1 Определение цены деления цилиндрического уровня нивелира по рейке
6.5.2 Определение цены деления шкалы микрометра нивелира
6.6.1 Рейки для нивелирования
6.6.2 Поверки и исследования реек
6.6.3 Определение стрелки прогиба рейки
6.6.4 Поверка перпендикулярности плоскости пятки к оси рейки
6.6.5 Определение разности высот нулей шкал реек
6.7. Нивелирование II класса
6.8. Особые случаи высокоточного нивелирования
6.9. Основные источники ошибок нивелирования
Раздел 1. Фигура Земли и система координат
#1.1. Понятие о фигуре Земли. Уровенные поверхности
Уровенной называют такую поверхность, которая в каждой своей точке перпендикулярна к направлению отвесной линии и имеет постоянный потенциал Fтяж.
Уровенных поверхностей может быть сколько угодно. В общем случае уровенные поверхности не параллельны друг другу. Уровенная поверхность никогда не пересекается. Каждая уровенная поверхность образует замкнутую фигуру без разрывов и складок, которая имеет на столько сложную конфигурацию, что математически не выражается.
Основная (средняя) уровенная поверхность – поверхность совпадающая со средней поверхностью мирового океана.
Геоид – образованная основной уровенной поверхностью замкнутая фигура принимаемая за обобщенную поверхность Земли.
Для точного определения поверхности геоида какой-либо точки необходимо выполнить комплекс измерений, непосредственно на поверхности геоида. Что практически не возможно, либо в соответствующей точке на физической поверхности Земли с учетом распределения масс в этом месте, что также не предоставляется возможным. По этой причине было предложено вместо поверхности геоида использовать квазигеоид, – поверхность близкая к поверхности геоида, определяемая только по результатам измерений на земной поверхности без привлечения данных по распределению масс.
Максимальное отклонение квазигеоида от геоида 4 м, но большинство считает, что 2 м.
#1.2. Общеземной эллипсоид и референц-эллипсоид
 Из-за сложности геоида эта поверхность математически не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения – близкой по форме геоиду, но математически правильной поверхности, на которую можно перенести результаты измерений выполненных на физической поверхности Земли.
Из-за сложности геоида эта поверхность математически не выражается, поэтому на ней нельзя решать геодезические задачи. Для решения таких задач взамен поверхности геоида принимают поверхность эллипсоида вращения – близкой по форме геоиду, но математически правильной поверхности, на которую можно перенести результаты измерений выполненных на физической поверхности Земли.
Земной эллипсоид – эллипсоид вращавшийся вокруг малой оси.
Чтобы на поверхности можно было работать, необходимо знать его основные параметры:
a – большая полуось, a = OE
b – малая полуось, b = OP
α – полярное сжатие, α = (a-b)/a
e – эксцентриситет, 
Для определения этих параметров выполняются градусные измерения, которые изначально сводились к определению длины дуги меридиана в 10 градус, а в настоящее время превратились в сложный комплекс астрономо-геодезических, гравиметрических и спутниковых измерений с привлечением данных из других смежных наук.
Различают общеземной эллипсоид, который наилучшим образом согласуется с поверхностью геоида в целом и референц-эллипсоид, который наилучшим образом согласуется с геоидом на ограниченной части его поверхности.
Требования к общеземному эллипсоиду:
1) центр должен совпадать с центром масс Земли
2) Плоскость экватора должна совпадать с плоскостью земного экватора
3) Объем должен быть равен объему геоида
4) Σh2=min
5) ΣU2=min
Требования к референц-эллипсоиду:
1) Ось вращения должна быть II оси вращения Земли
2) Плоскость экватора должна быть II плоскости земного экватора
3) Σh2=min, ΣU2=min – для ограниченной территории
Объем может быть не равен объему геоида
#1.3. Основные линии и плоскости земного эллипсоида

Нормаль – перпендикуляр к поверхности данной точки (эллипсоида).
Все плоскости проходящие через нормаль называются нормальными плоскостями, а сечение ими поверхности эллипсоида – нормальным сечением.
Все сечения не являющиеся нормальными называются наклонными сечениями.
Нормальная плоскость ┴ плоскости меридиана называется плоскостью 1-го вертикала.
1-вертикал – плоскость перпендикулярная к меридиану
Меридиан и 1-вертикал – главные нормальные сечения.
#1.4. Уклонения отвесных линий
(см. рис.)
В общем случае поверхность геоида и поверхность эллипсоида не II между собой.
Уклонением отвесной линии называется угол «u» образованный при несовпадении отвесной линии проведенной в точке на земной поверхности ┴-но геоиду с проведенной в этой же точке ┴-но к эллипсоиду нормалью.
Уклонением отвесной линии от нормали к общеземному эллипсоиду называется абсолютным, а от нормали к референц-эллипсоиду – относительным.
Уклонение отвесных линий «u» в любой точке для практических целей обычно рассматривают не целиком, а в проекции на плоскость меридиана ξ и на плоскость 1-го вертикала η.
#1.5. Системы координат
Координаты – угловые и линейные величины однозначно определяющие положение точки на какой-либо поверхности или в пространстве относительно принятого их счета.
На сферической поверхности наиболее удобными являются географические координаты (широта и долгота) отсчитываемые от поверхности экватора и начального меридиана в виде дуг, которым соответствуют центральные углы.
Из-за неправильности форм Земли и неравномерности распределения масс в ней географические координаты не подходят для использования в геодезических работах. Поскольку в общем случае отвесная линия в данной точке не совпадает с нормалью, плоскость меридиана проходящая через отвесную линию параллельна оси вращения Земли и не совпадает с плоскостью геодезического меридиана, проходящего через нормаль и ось вращения эллипсоида.
В результате этого несовпадения различают астрономическую и геодезическую системы координат.
Астрономические координаты точки определяются из непосредственных наблюдений небесных тел, выполненных на этой точке совершенно и независимо от других точек.
Астрономической широтой точки называется угол, отсчитываемый от плоскости экватора в плоскости астрономического меридиана до отвесной линии в этой точке, или дуга астрономического меридиана от экватора до точки.
Астрономической долготой точки называется двугранный угол, отсчитываемый от плоскости гринвичского астрономического меридиана до плоскости астрономического меридиана данной точки, или дуга экватора между этими меридианами.
Астрономическим азимутом направления называется двугранный угол, отсчитываемый от северной части плоскости астрономического меридиана данной точки по часовой стрелке до отвесной плоскости содержащей данное направление.
Геодезические координаты точки получаются по средствам передачи их от какого-то исходного пункта через геометрические построения на поверхности эллипсоида.
Геодезической широтой β называется угол, отсчитываемый от плоскости экватора в плоскости геодезического меридиана до нормали проведенной точки, или дуга геодезического меридиана от экватора до точки.
Геодезической долготой L называется двугранный угол, отсчитываемый до плоскости геодезического меридиана точки от плоскости геодезического меридиана принятого за начальный, или дуга экватора между этими меридианами.
Геодезическим азимутом направления называется двугранный угол, отсчитываемый от северной части плоскости геодезического меридиана точки по часовой стрелке до нормальной плоскости содержащей данное направление.
Связь геодезических координат с астрономическими осуществляется через составляющие отклонения отвеса в данной точке:
βм=jм-ξм
Lм=αм-ηмsecjм
Δмк=αмк+(Lм-αм)*secjм
#1.6. Основные системы высот
 Высотой точки называется ее отстояние от поверхности принятой за начальную.
Высотой точки называется ее отстояние от поверхности принятой за начальную.
В высшей геодезии три основные системы высот:
Ортометрическая высота точки – ее отстояние от поверхности геоида по отвесной линии.
Геодезическая высота точки – ее отстояние от поверхности референц-эллипсоида по нормали.
Нормальная высота точки – ее отстояние от поверхности квазигеоида по нормали.
Работы выполняются только в ортометрических системах высот.
Раздел 2. Государственная геодезическая сеть (ГГС)
#2.1. ГГС. Сущность. Назначение. Виды
ГГС – система закрепленных на местности пунктов, положение которых определено в единой системе координат и высот.
Все геодезические сети можно разделить по следующим признакам:
По территориальному признаку:
1) глобальная
2) национальные (ГГС)
3) сети специального назначения (ГССН)
4) съемочные сети
по геометрической сущности:
1) плановые
2) высотные
3) пространственные
Глобальные сети создаются на всю поверхность Земли спутниковыми методами и являются пространственными с началом координат в центре масс Земли. (ПЗ-90).
Национальные сети делятся на: ГГС с определением координат в СК-95 в проекции Гаусса-Крюгера на плоскости и на ГНС с определением нормальных высот в Балтийской системе, т.е. от 0 (нуля) Кронштадтского футштока.
ГССН создаются в тех случаях, когда дальнейшее сгущение пунктов ГГС экономически нецелесообразно или когда требуется особо высокая точность геодезической сети. В зависимости от назначения эти сети могут быть плановыми, высотными, планово-высотными и даже пространственными и создаваться в любой системе координат.
Съемочные сети являются обоснованием для выполнения топосъемок и создаются обычно планово-высотными.
2.1.2 ГГС. Классификация. Понятие о плотности и точности
ГГС, созданная по состоянию на 1995 года, объединяет в одно целое:
астрономо-геодезические пункты космической геодезической сети (АГП КГС),
доплеровскую геодезическую сеть (ДГС),
астрономо-геодезическую сеть (АГС) 1 и 2 классов,
геодезические сети сгущения (ГСС) 3 и 4 классов.
Пункты указанных построений совмещены или имеют между собой надежные геодезические связи.
ГГС включает в себя геодезические построения различных классов точности:
фундаментальную астрономо-геодезическую сеть (ФАГС)
высокоточную геодезическую сеть (ВГС),
спутниковую геодезическую сеть 1 класса (СГС-1)
Плотность ГГС по территории:
| масштаб | 1 пункт на: | сред. расст. |
| 1:25000 | 50-60 км2 | 7-8 км |
| 1:10000 | 50-60 км2 | 7-8 км |
| 1:5000 | 20-30 км2 | 5-6 км |
| 1:2000 | 5-15 км2 | 2-4 км |
Ошибка длины: 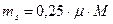 ,
,
где m – графическая ошибка длины на карте, M – знаменатель масштаба.
2.1.3 Астрономо-геодезическая сеть (АГС)
АГС-1 построена в виде полигонов периметром» 800 км, образованных звеньями триангуляции или в редких случаях полигонометрии, длиной < 200 км, расположенных вдоль меридианов и параллелей.
Звено триангуляции состоит из ряда смежных треугольников, близких к равносторонним, с углами > 400 и сторонами > 20 км.
Базисные стороны – стороны между углами полигонов, длиной 170-200 км, измеряемые для масштабирования сети.
Астропункты Лапласа – пункты на концах базисных сторон, на них измерены астрономические широты, долготы и азимуты. Широты и долготы полученные с помощью координирования, а азимуты – ориентирования.
Звенья полигонометрии АГС-1 заменяют ряды триангуляции в случае технической необходимости и экономической целесообразности и представляет вытянутый ход не более чем из 10 сторон, длиной 20-25 км.
АГС-2 построена основном методом триангуляции в виде сплошных сетей треугольников заполняющих полигоны АГС-1, с углами > 300 и средней длиной сторон от 7 до 20 км.
В АГС-2 базисные стороны должны быть не реже чем через 25 треугольников и обязательно в центре полигона 1 класса.
АГС-2 созданная методом полигонометрии имеет вид ходов, опирающихся на пункты 1 класса и образующих в пересечении сплошную сеть 3-5 треугольников.
Точность измерений в АГС-1 и АГС-2:
| АГС-1 | АГС-2 | |
| СКО измеренного угла, mb | 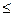 0,74" 0,74"
| 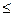 1,06" 1,06"
|
СКО базисной стороны, 
| 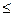 
| 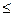 
|
СКО линейных измерений, 
| 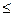 
| 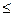 
|
| СКО астрономической широты, mj | 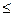 0,3" 0,3"
| 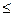 0,3" 0,3"
|
| СКО астрономической долготы, ml | 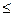 0,043s 0,043s
| 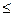 0,043s 0,043s
|
| СКО астрономического азимута, ma | 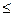 0,5" 0,5"
| 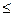 0,5" 0,5"
|
#2.1.4 Геодезические сети сгущения 3-4 класса (ГСС)
Геодезические сети сгущения 3 и 4 классов включают в себя около 300 тысяч пунктов. Они служат для сгущения 2 класса и могут создаваться, в зависимости от местных условий, методами триангуляции, полигонометрии и трилатерации.
В трилатерации пункты 3 и 4 класса определяются путем “вставки” отдельных пунктов или систем в треугольнике 2 класса. Треугольники 3 или 4 класса имеют углы не менее 200 и стороны 5-8 км и 2-5 км соответственно.
Полигонометрия, построенная проложением ходов опирающихся на пункты высших классов со звеньями не более чем из 3 сторон, каждая длиной не менее 3 км в 3 классе и не менее 2 км в 4 классе.
Для повышения жесткости сетей сгущения пункты или системы в триангуляции, а также ходы в полигонометрии связаны между собой сторонами, если расстояние между ними менее 4 км в 3 классе и 3 км в 4 классе.
Точность измерений характеризуется следующими СКО:
| 3 класс | 4 класс | |
| СКО измеренного угла, mb | 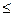 1,5" 1,5"
| 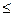 2,0" 2,0"
|
СКО линейных измерений, 
| 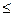 
| 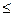 
|
#2.1.5 Понятие об ориентирных пунктах ГГС
На каждом пункте существующей ГГС установлены два ориентирных пункта, пронумерованные от направления на север по часовой стрелке, на расстоянии от центра пункта не менее 500 м в открытой и 250 м в занесенной местности, с обеспечением видимости на них непосредственно с центра.
В качестве одного из ОРП мог использоваться вертикальный местный предмет, видимый до основания на расстоянии не более 3 км.
Основное назначение ОРП – это азимутальная, т.е. угловая привязка полигонометрии и других построений без подъема на знак.
Высоты всех пунктов ГГС определены в основном тригонометрическим нивелированием по сторонам сети от пунктов, принятых за опорные, которые определены геометрическим нивелированием и расположены не реже чем 3 стороны полигонометрии или 75 км в сети триангуляции.
Раздел 3. Точные угловые измерения
3.1. Точный оптический теодолит типа Т2 (3Т2КП)
По действующему ГОСТУ теодолит типа Т2 по точности относится к классу точных теодолитов (mb = 1.5"-2.0").
Точный оптический теодолит типа Т2 предназначен для угловых измерений в ГСС 3-4 классов и ГССН со средней квадр. ошибкой (СКО) mb = 1.5"-2.0" и более, а также для инженерных работ соответствующей точности.
Увеличение зрительной трубы: не менее 25х (в 3Т2КП 30х)
Цена деления лимба: 35'
Цена деления оптического микрометра: 1"
Цена деления цилиндрического уровня на ГК: 15"
Масса: 4,7 кг.
Прибор имеет оптический центрир.
Отсчетная система – оптический микрометр.
3.2. Основные поверки точного оптического теодолита типа Т2
Поверки точного оптического теодолита типа Т2 выполняются для выявления отклонений от геометрических и оптико-механических условий, предусмотренных конструкцией прибора. Выявление недопустимых отклонений устраняются путем юстировки.
Порядок выполнения поверок:
1) поверка устойчивости штатива
2) поверка и регулировка хода подъемных винтов
3) поверка работы наводящих устройств
4) поверка цилиндрического уровня на алидаде ГК
5) поверка накладного уровня
6) поверка правильности вращения алидады ГК
7) поверка изображений в поле зрения оптического микрометра
8) поверка сетки нитей
9) поверка коллимационной ошибки (2С)
10) поверка положения оси вращения зрительной трубы
11) поверка места зенита (MZ)
12) поверка предварительного определения
13) поверка оптического центрира
Для теодолита с компенсатором ВК:
14) поверка круглого уровня
15) поверка работы компенсатора
3.3.1 Поверка цилиндрического уровня на алидаде ГК
Ось цилиндрического уровня должна быть перпендикулярна оси вращения прибора.
Поверка выполняется поворотом на 1800 алидадной части прибора, заранее приведенного в рабочее положение. Если отклонение пузырька в 0-пункте превысило 1 деление, то выполняется юстировка – перемещением пузырька на половину дуги отклонения, путем вращения юстировочного винта уровня с помощью отвертки.
3.3.2 Поверка установки сетки нитей
Вертикальная нить сетки и ось биссектора должны находится в коллимационной плоскости зрительной трубы.
Коллимационной называется плоскость, проходящая через центр сетки нитей перпендикулярно оси вращения трубы. Выполняется проведением вертикальной нити и биссектора на хорошо видимой точке расположенной. на высоте прибора.
Условие выполнено если точка осталась в пределах биссектора.
3.3.3 Поверка коллимационной ошибки
Визирная ось зрительной трубы должна быть перпендикулярна оси вращения трубы.
Выполняется визированием и взятием отсчетов по ГК при КЛ и КП на удаленную хорошо видимую точку, расположенную на высоте прибора. Для повышения точности, измерения повторяются на другую точку и считаются качественными, если разница результатов не превышает 8".
2С1 = L1-(R1+-180)
2C2 = L2-(R2+-180)
D2С = ½2С1 – 2С2½ ≤ 8"
2С = (2С1 + 2С2)/2;
½2С½ ≤ 20"
3.3.4 Поверка места зенита
MZ не имеет большую величину и постоянно.
MZ – отсчет по вертикальному кругу при зенитном направлении визирной оси и приведенном в нуль-пункт пузырька уровня ВК или работающем компенсаторе.
Выполняется визированием и взятием отсчетов по ВК при КЛ и КП на удаленную хорошо видимую точку, расположенную на высоте прибора. Для контроля и повышения точности, измерения повторяют на другую точку и считают качественными если разница результатов не превысит 10".
MZ1 = (L1+R1-360)/2
MZ2 = (L2+R2-360)/2
DMZ = ôMZ1-MZ2ô ≤ 10"
MZ = (MZ1+MZ2)/2
ôMZô ≤ 10"
3.3.5 Поверка положения оси вращения зрительной трубы
3.3.6 Поверка оптического центрира
3.3.7 Поверка оптического компенсатора
Компенсатор должен работать при отклонении оси вращения теодолита от отвесного положения до 3'.
Для поверки прибор устанавливают трубой над одним из подъемных винтов. Наводят горизонтальную нить на точку и берут отсчет по ВК. Вращением подъемного винта находящегося под трубой наклоняют теодолит в коллимационной плоскости на 1/2 деления круглого уровня. Горизонтальную нить возвращают на точку наводящим винтом трубы и снова берут отсчет по ВК.
Разность отсчетов не должна превышать 10".
Юстировка в мастерской.
3.4.1 Исследования теодолита
Исследования проводятся после поверок и юстировок с целью определения индивидуальных характеристик прибора, для установления его пригодности к выполнению планируемых работ.
Перед началом полевых работ исполнитель должен исследовать:
1) правильность работы оптического микрометра:
а) систематические ошибки,
б) ошибки совмещения штрихов
2) эксцентриситет лимба
3) эксцентриситет алидады
4) реон оптического микрометра
Для выявления систематических ошибок микрометра, разными его частями измеряют малый угол и сравнивают результаты измерений. Ошибка совмещения штрихов определяется по разностям получившихся в отсчетах при двойном совмещении штрихов.
3.4.2 Эксцентриситет лимба и алидады
Эксцентриситет лимба – несовпадение его геометрического центра, т.е. центра круга делений с осью вращения лимба.
Характеристикой качественного исследования служит величина отклонения построенного по взятым отсчетам графика от синусоиды. А величина эксцентриситета. характеризуется амплитудой графика.
Эксцентриситет алидады – несовпадение оси вращения алидады с геометрическим центром лимба.
Оценка точности также.
3.4.3 Реон оптического микрометра
Реон оптического микрометра – разность между номинальной ценой ½ деления лимба и его величиной измеренной микрометром.
Для определения реона на предусмотренных программой установки лимба выполняют совмещение штрихов и берут отсчеты, по которым вычисляют значение реона на каждой установке.
r верх. - r ниж. = ôDrô;
ôDrô ≤ 1" Если условие выполнено, то вычисляется сам реон:
r = (r вер + r ниж)/2
Если ôrô ≥ 1" то регулировка в мастерской, либо введение поправок.
А если ôDrô превышает 1", то прибор сразу нести в ремонт.
Раздел 4. Полевые работы на пунктах геодезических сетей
4.2. Способ измерения отдельного угла
Способ часто применяется при 2-х направлениях на пункты (полигонометрия).
 Методика измерений:
Методика измерений:
1) при КЛ примерно наводят трубу на визирную цель задней точки и устанавливают на лимбе начальный отсчет данного приема.
2) поворачивают алидаду на 30o-40o против часовой стрелки.
3) вращением по часовой стрелке точно наводят трубу на левую визирную цель и при 2-х совмещениях штрихов берут отсчеты по микрометру с допустимым расхождением не более 2".
4.77. производство точных угловых измерений. Приборы, методы и программы угловых измерений на пунктах ГСС 3-4 класса.
В зависимости от количества направлений на пункте угловые измерения выполняются способом отдельного угла или способом угловых приемов, при этом количество выполняемых приемов зависит от класса пунктов и точности приемов и для теодолита Т2 составляют:
| Класс Метод | 3класс (1,5") | 4класс (2,0") |
| Трилатерация | 12приемов | 6приемов |
| полигонометрия |
Для достижения максимальной независимости измерений, измерение в каждом приеме выполняются на другой части лимба, для чего между приемами лимб переставляют на величину δ=180º/m +i/2, где m-число приемов
i-цена деления лимба.
Допуски и правила перенаблюдений.
При точных угловых наблюдениях допуски как правило не зависят от вида работ и класса пункта, а устанавливаются в зависимости только от точности прибора и для теодолита типа Т2 составляют: не замыкание в полу приеме должно не превышать 8секунд, колебания двойной колемационной ошибкой в приеме <=12сек, расхождение значения угла между полу приемами Δβ’=Δ(Л-П)<=8’’, колебание значений направлений или углов между приемами Δ М<=8’’; Δβ<=8’’.
Первые два допуска называют «внутренними» и если в приеме они выполняются то прием считается законченным и независимо от его конечного результата не может быть переделан до окончания всей программы.
Если в процессе выполнения приема, выявлено какое либо нарушение допусков, то измерения должны быть прекращены, прием вычеркнут с указанием причины и тут же переделан с измерением начальной установки примерно на 1 минуту.
При недопустимых расхождениях в значении одного и того же угла или направления между приемами программы, вопрос об их переделке может быть решён только после всей программы. В случае недопустимого отклонения значения в каком либо приеме от всех остальных приемов программы, данный прием может считаться явно ошибочным и может быть переделан на той же табличной установке лимба под своим номером с пометкой повторно или бис.
В случае допустимости расхождения данного приема с одним или несколькими другими приемами программы переделке подлежат приемы с наибольшими и наименьшими значениями.
Всего в программе может быть переделано не более 1/3 приемов.
Программа измерения зенитных расстояний на пунктах 3-4класса всегда состоит из 4-х приемов в которых независимо от класса пункта и точности прибора колебание MZ в приеме и Z между приемами не должно превышать 15’’. Переделки выполняются соответственно по окончании приема или по окончании всей программы отдельно по каждому направлению.
Раздел 5. Геодезические сети специального назначения (ГССН)
#5.1.1. Общие сведения о ГССН
ГССН – главная геодезическая основа для крупномасштабных (1:2000 и крупнее) съемок, а также для других работ, требующих соответствующей точности. ГССН создаются в тех случаях, когда дальнейшее сгущение пунктов ГГС экономически нецелесообразно или когда требуется особо высокая точность геодезической сети.
Плотность пунктов ГССН:
на незастроенных территориях: до 1п. на 1км2
на застроенных территориях: до 4п. на 1км2
на территориях крупных инженерных сооружений и на пром. площадках: до 8п. на 1км2
Точность определения пунктов ГССН зависит в основном от масштаба съемки и характеризуется СКО взаимного положения смежных пунктов: 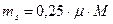
ГССН классифицируется на сети 1 и 2 разрядов и в зависимости от полевых условий могут создаваться методами триангуляции, трилатерации, полигонометрии или их сочетанием, с опорой на пункты ГГС.
Поскольку в соответствии с основным назначением ГССН строится как правило на застроенных и подлежащих застройке территориях основным методом ее создания является полигонометрия.
#5.1.2. Построение ГССН методом полигонометрии
Построение ГССН методом полигонометрии производится проложением отдельных ходов, систем ходов с угловыми точками или систем замкнутых полигонов с опорой на пункты ГГС. В отличие от других методов построения ГССН полигонометрия классифицируется на: а) 2 разряд, б) 1 разряд, в) 4 класс, который имеет пониженную по сравнению с ГГС точность и строится там где ГГС 4 класса отсутствует для связи разрядных сетей с ГГС 3 класса.
Если между параллельными ходами расстояние не превышает 2,5км в 4 классе и 1,5км в 1 разряде то они должны быть связаны между собой ходом перемычкой той же точности.
Проложение висячих ходов запрещено, а замкнутые разрешены в 1 и 2 разрядах только в виде исключения, при условии автономного определения с точностью 5’’ азимутов двух смежных сторон в самом слабом месте хода.
Определение высот пунктов в полигонометрии выполняется только геометрическим нивелированием т.е. горизонтальным лучом с учетом возможности их использования в качестве высотных при создании съемочного обоснования.
#5.1.3. Закрепление пунктов ГССН на местности
Закрепление пунктов ГССН производится везде, где это возможно, стенными знаками, которые закладываются в долговременные здания и сооружения на высоте не менее 0,3 м над землей, в местах, удобных для привязки и постановки нивелирной рейки.
Поскольку на стенной знак прибор не поставить в близи от него устанавливают временный рабочий центр, который является точкой прокладываемого хода.
На незастроенной территории устанавливают грунтовые знаки, в виде центров, состоящих из бетонного якоря и пилона. Глубина закладывания 1 м. Для области многолетней мерзлоты также как и в ГСС – с глубиной на 1 м. ниже границы отстаивания. при закладке грунтовых реперов на застроенной территории, их верхняя часть закрепляется предохранительным колпаком с крышкой.
В качестве наружных знаков могут быть установлены деревянные или металлические пирамиды 3х или 4х-гранные, высотой от 3 м.
#5.2.1 Угловые измерения на пунктах полигонометрии ГССН
Основным способом угловых измерений в ГССН является способ измерения отдельного угла. Основным прибором является точный оптический теодолит типа Т2 или другие высокоточные теодолиты. Кол-во приемов в программе измерений на пункте ГССН зависит от точности прибора и разряда сети и оставляет:
количество приемов в программе:
| Теодолит | 4 класс | 1 разряд | 2 разряд |
| Т1 | |||
| Т2 | |||
| Т5 | - | - |
Приборы, программы и методы должны обеспечивать угловые измерения с СКО не превышающей соответственно 2”, 5”, 10”. При этом допуски при измерениях составляют:
| Т2 | Т5 | |
| незамыкание в полуприемах | 8" | 12" |
| Колебания 2С в приеме | 12" | - |
| Расхождение направлений между приемами | 12" | - |
| Расхождение угла между полуприемами | 8" | 12" |
| Расхождение угла между приемами | 8" | 12" |
Особенностью угловых измерений в ГССН является необходимость визирования на небольшие и при этом различающиеся между собой расстояния, что ведет к изменению ошибки визирования, т.е. к ее неравноточности.
Для повышения точности визирования и достижения ее примерной равноточности в качестве ее визирных целей применяют специальные марки, которые обеспечивают одинаковую точность визирования независимо от расстояния.
#5.2.2 Линейные измерения в полигонометрии ГССН
Основным способом линейных измерений в ГССН являются измерения электронными приборами – светодальномерами группы Т или тахеометрами. Полученные дальномерные расстояния должны быть исправлены поправками:
1) за приведение к горизонту
2) за приведение к референц-эллипсоиду
3) за приведение на плоскость в проекции Гаусса.
В полигонометрии 2 разряда разрешается выполнить измерения компарированной стальной рулеткой на весу по кольям высотой ~0,5м выставленным по теодолиту в створе линии и разбивающим ее на пролеты чуть меньше длины рулетки. При измерениях натяжение динамометром должно быть не менее 5 кг и равно натяжению при компарировании.
Приведение к горизонту выполняется отдельно по каждому пролету по результатам нивелирования кольев. В измеренную длину вводят поправки за компарирование и температуру.
В результате линейных измерений должна быть обеспечена относительная ошибка хода не более  в 4 классе,
в 4 классе,  во 2 разряде и
во 2 разряде и  в 1 разряде.
в 1 разряде.
Относительная разность в измерениях не должна превышать 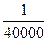 ,
,  ,
, 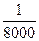 .
.
#5.2.3. Трехштативный метод
Из-за малой длины сторон очень большое влияние на невязки ходов и полигонов ГССН оказывают ошибки центрирования приборов и визирных целей.
При центрировании прибора и визирной цели каждый раз на всех точек хода возникает неоднозначность измерения углов, которая повлечет за собой угловую невязку хода, при условии, что другие ошибки отсутствуют.

 Для уменьшения этого влияния применяют трехштативный метод – при котором, на каждой точке хода штатив со стандартной подставкой центрируется один раз и в эту подставку поочередно устанавливают переднюю визирную цель, прибор и заднюю визирную цель, между которыми и выполняют измерения.
Для уменьшения этого влияния применяют трехштативный метод – при котором, на каждой точке хода штатив со стандартной подставкой центрируется один раз и в эту подставку поочередно устанавливают переднюю визирную цель, прибор и заднюю визирную цель, между которыми и выполняют измерения.
В полученном при этом “воздушном” полигоне при условии отсутствия всех ошибок, кроме ошибки центрирования, невязка при уравнивании полигона будет равно 0 (нулю). Тогда координаты каждой точки хода будут получены с ошибкой полученной при центрировании именно в этой точке.
Кроме указанных преимуществ применение метода при наличии 4-го штатива дает значительное повышение производительности труда за счет экономии времени на центрирование.
#5.3.1. Передача координат на стенной знак. Линейная засечка
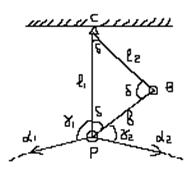 Применяется при небольших расстояниях до центра и является самым простым методом.
Применяется при небольших расстояниях до центра и является самым простым методом.
Дано: XP, YP, a1, a2
Измерено: b, l1,, l2,, c1, c2
Из решения треугольника PCB по его сторонам вычисляем углы d (см. формулы трилатерации) и их невязку W=Σd-180º.
Считая невязку треугольника следствием ошибок линейных измерений выполняют уравнивание этого треугольника, в результате чего получают вероятнейшие значения его углов и сторон: l01, l02 , b0, δ01 , δ02, δ03.
Вычисляют для контроля дважды aPC = a1+γ1, aPC = a2-γ2-d.
Усредняют aPC (ср.). По вероятнейшим значениям l01 и a0PC решают ПГЗ.
#5.3.2. Передача координат на стенной знак. Угловая засечка
Применяется при значительных расстояниях до центра или невозможности линейных измерений по другим причинам.
 Дано: XP, YP, a1, a2
Дано: XP, YP, a1, a2
Измерено: b1, b2, b, c1, c2
Вычисляют: d = 1800-(b1+b2),  (по т. синусов)
(по т. синусов)
Для повышения точности l измеряют из другого построенного базиса.
Сравнивают результаты и при допустимости усредняют (lср .)
Вычисляют для контроля дважды aPC = a1+γ1, aPC = a2-γ2.
Усредняют aPC (ср.).
Далее по значениям lср и aPC (ср) решают ПГЗ.
#5.3.3. Передача координат на стенной знак. Полярный способ
Применяется при передачи координат на ориентирную систему из 3-х, 2-х или 1-го стенных знаков.
 Дано: XP, YP, a1, a2
Дано: XP, YP, a1, a2
Измерено: l1,, l2,, d, b, c1, c2
Вычисляют:  (по т. косинусов)
(по т. косинусов)
Имея измеренную величину d и считая ее правильной, можно выполнить уравнивание системы и получить поправки в l1 , l2 , b и их уравненное значение l01 , l02 , b0.
Вычисляют для контроля дважды aPC1 =a1+γ1, aPC2 =a2-γ2.
aPC2-aPC1 ≈ b0
Da = (aPC2-aPC1) - b0
Уравнивают aPC2 и aPC1, после чего (a0PC2-a0PC1) - b0 = 0
Решаем ПГЗ по a0PC1 и a0PC2.
По полученным координатам с1 и с2 находим для контроля d.
#5.3.4. Передача координат на стенной знак. Редуцирование
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2553; Нарушение авторских прав?; Мы поможем в написании вашей работы!