Приклад. 2. Визначники другого і третього порядків, їх властивості

План

1. Основні поняття.

2. Визначники другого і третього порядків, їх властивості

3. Мінори та алгебраїчні доповнення.

4. Обчислення визначників

5. Правило Крамера.

1. Основні поняття

Предметом розгляду лінійної алгебри для економістів є насамперед теорія систем лінійних рівнянь, які в загальному вигляді можна подати так:

(1.1)

Система (1.1) називається системою m лінійних рівнянь з невідомими (змінними), де x ₁, x ₂,..., x_n — невідомі; a_ij 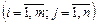— коефіцієнти системи рівнянь; b_i 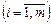— вільні члени, або праві частини системи рівнянь. Якщо всі b_i = 0 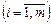, то система лінійних рівнянь називається однорідною.

Розв’язком системи рівнянь (1.1) є множина таких чисел k ₁, k ₂, ..., k_n, у результаті підставляння яких замість відповідних невідомих x ₁, x _2, ..., x_n у кожне з рівнянь системи (1.1) останні перетворюються на правильні числові рівності.

Якщо система рівнянь не має жодного розв’язку, вона називається несумісною, а якщо має хоча б один розв’язок — сумісною. Сумісна система рівнянь називається визначеною, якщо вона має єдиний розв’язок, і невизначеною, якщо розв’язків більш як один.

2. Визначники другого і третього порядків, їх властивості

Розглянемо спочатку системи рівнянь, в яких кількість невідомих і кількість рівнянь рівні між собою, тобто m = n. Нехай, наприклад, n = m = 2, тоді маємо систему двох лінійних рівнянь з двома невідомими:

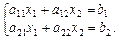
Визначником другого порядку називається вираз

.

.

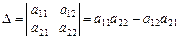Якщо n = m = 3, то маємо систему трьох лінійних рівнянь з трьома невідомими:

Визначником третього порядку називається вираз:

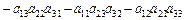. (1.2)

Для запам’ятовування правила обчислення визначника третього порядку пропонуємо таку схему (правило трикутників):

Позначимо точками елементи визначника, тоді доданки зі знаком «плюс» — це добутки елементів a ₁₁, a ₂₂, a ₃₃, розміщених на головній діагоналі визначника, і добутки елементів a ₁₃, a ₂₁, a ₃₂ і a ₁₂, a ₂₃, a ₃₁, розміщених у вершинах рівнобедрених трикутників, основи яких паралельні головній діагоналі. Зі знаком «мінус» беруться доданки, що є добутками елементів a ₁₃, a ₂₂, a ₃₁, розміщених на сторонній діагоналі визначника, та у вершинах рівнобедрених трикутників, основи яких паралельні сторонній діагоналі визначника — a ₁₁, a ₂₃, a ₃₂ і a ₁₂, a ₂₁, a ₃₃.

Запропонуємо ще одне правило обчислення визначника третього порядку (правило Саррюса).

У початковому визначнику за третім стовпцем запишемо ще раз перший і другий стовпці:

Для знаходження визначника за цим правилом треба утворити зі знаком «плюс» алгебраїчну суму добутків елементів, розміщених на головній діагоналі визначника, і на діагоналях, паралельних їй, а зі знаком «мінус» — добутків елементів, розміщених на сторонній діагоналі, та на діагоналях, паралельних їй.

Визначник:

,

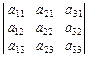рядки якого є стовпцями попереднього визначника, є транспонованим щодо визначника (1.2).

Властивість 1. Визначник не змінюється в результаті тран­спонування.

З властивості 1 випливає, що будь-яке твердження, котре справджується для рядків визначника, справджується і для його стовпців, і навпаки.

Властивість 2. Якщо один із рядків визначника складається лише з нулів, то такий визначник дорівнює нулю.

Властивість 3. Якщо поміняти місцями будь-які два рядки визначника, то його знак зміниться на протилежний.

Властивість 4. Визначник, який має два однакові рядки, дорівнює нулю.

Властивість 5. Якщо елементи будь-якого рядка визначника помножити на стале число С, то й визначник помножиться на С.

З останньої властивості випливає, що спільний множник елементів рядка можна виносити за знак визначника.

Властивість 6. Визначник, який має два пропорційні рядки, дорівнює нулю.

Властивість 7. Якщо всі елементи будь-якого рядка визначника можна подати у вигляді суми двох доданків, то такий визначник дорівнює сумі двох визначників, у яких елементами цього рядка будуть відповідно перший доданок у першому визначнику і другий доданок у другому визначнику, а решта елементів будуть ті самі, що й у початковому визначнику.

Властивість 8. Визначник не зміниться, якщо до елементів будь-якого рядка додати відповідні елементи довільного іншого рядка, попередньо помножені не деяке число.

3. Мінори та алгебраїчні доповнення

Нехай визначник має n рядків і n стовпців. Мінором k-го порядку k [1; n –1] називається визначник, утворений з елементів, розміщених на перетині будь-яких k рядків і k стовпців визначника. Зрозуміло, що мінор першого порядку — це будь-який елемент визначника.

Приклад. Утворити кілька мінорів другого і один мінор третього порядку такого визначника:

.

, , ,..., .

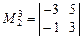Мінори , , другого порядку утворюються з елементів, розміщених на перетині першого, другого рядків; першого, другого стовпців; третього, четвертого рядків; першого, третього стовпців; другого, четвертого рядків; третього, четвертого стовпців. Мінор третього порядку утворюється з елементів, розміщених на перетині другого, третього, четвертого рядків і першого, третього, четвертого стовпців.

Верхній індекс означає нумерацію мінорів; нижній індекс — порядок мінора.

Доповняльним мінором для мінора k -го порядку називається такий мінор, який лишається у визначнику після викреслювання тих k рядків і тих k стовпців, на перетині яких містяться елементи, що утворили мінор k -го порядку.

Нехай мінор k- го порядку утворено з елементів, розміщених на перетині i ₁, i ₂,..., i_k рядків і j ₁, j ₂,..., j_k стовпців.

Алгебраїчним доповненням до мінора k -го порядку є доповняльний мінор (n – k) - го порядку, узятий зі знаком 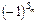, де 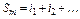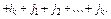Якщо сума 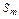номерів рядків і стовпців парна, то береться знак «+», якщо непарна — то знак «–».

Далі важливу роль відіграватиме алгебраїчне доповнення до мінора першого порядку. Нехай — будь-який елемент-мінор першого порядку у визначнику n -го порядку, тоді буде алгебраїчним доповненням до мінора 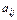. Тут 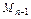— доповняльний мінор (n –1)-го порядку, утворений викреслюванням i -рядка і j -стовпця в початковому визначнику n -го порядку.

4. Обчислення визначників

Означення. Визначником n-го порядку називається число , яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпця на відповідні їм алгебраїчні доповнення:

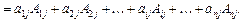(1.3)

Алгебраїчні доповнення, що входять до формули (1.3), за якою обчислюють визначник, є, у свою чергу, мінорами, узятими з відповідними знаками, тобто визначниками (n –1)-го порядку. Отже, обчислення визначника n -го порядку зводиться до обчислення n визначників (n –1)-го порядку.

Але з формули (1.3) випливає, що за наявності у визначнику нульових елементів відповідні алгебраїчні доповнення обчислювати не потрібно.

Згідно з властивістю 8, яка справджується для визначників будь-якого порядку, можна визначник перетворити так, щоб у його рядках або стовпцях усі елементи, крім одного, дорівнювали нулю. І тоді, розклавши визначник за елементами цього рядка або стовпця, зведемо задачу знаходження визначника n-го порядку до знаходження одного визначника n–1-го порядку.

Дата добавления: 2014-01-04