Дифракция при скользящем падении на решетку

Перед демонстрацией этого красивого эксперимента полезно ознакомить студентов с краткой теорий наклонного падения света на дифракционную решетку [12]. Пусть плоская волна падает на решетку с периодом d под углом 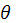(рис. 8.35).

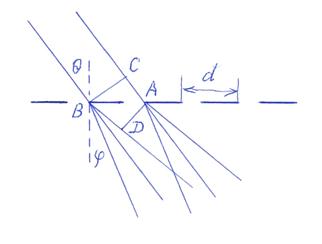
Рис. 8.35.Наклонное падение лучей на дифракционную решетку

Разность хода между соседними вторичными волнами в направлении φ равна

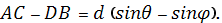(1)

Условие главных максимумов имеет вид

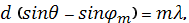(2)

где 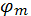– направления на главные максимумы m-го порядка.

Левую часть формулы (2) можно записать в виде

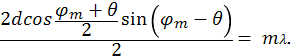(3)

Если d >> 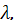то углы дифракции малы и Тогда вместо (3) имеем

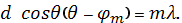(4)

Сравнивая с формулой для решетки при нормальном падении

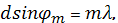(5)

видим, что отклонения дифрагированных максимумов от 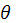вычисляются так же, как для нормального падения на решетку с периодом 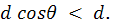Если 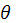близко к 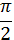, то имеет место весьма заметное уменьшение периода.

Для демонстрации берем рейку от зубчатой передачи (кремальеры) и освещаем ее излучением лазера (в данном случае удобен зеленый лазер мощностью около 20 мВт). На рис. 8.36 хорошо видна геометрия взаимного расположения лазера и рейки.

Рис. 8.36. Скользящее падение на рейку.

Рис. 8.37. Дифракционный спектр.

Демонстрация проводится в хорошо затемненной аудитории. На экране (стене аудитории) виден отчетливый дифракционный спектр со многими порядками (рис. 8.37). Наиболее яркое пятно – это нулевой порядок дифракции.

После этой демонстрации уместно рассказать студентам, что с особенностями скользящего падения на дифракционную решетку физики-экспериментаторы столкнулись, когда начали интенсивно изучать рентгеновский диапазон электромагнитного излучения. В этом диапазоне оптические решетки являются слишком грубыми, для них d/ 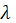~ 1000. Вот тогда-то и применили косое падение излучения. Например, в 1925 году Комптон и Дьюэн получили дифракцию рентгеновских лучей на решетке с d ~ 0,02 мм.

Дата добавления: 2014-01-04