Угол Брюстера

Рассказывают, что поляризацию света открыл Э. Малюс (1775 - 1812), рассматривая через кристалл исландского шпата окна расположенного напротив его дома Люксембургского дворца. Вращая этот кристалл, который служил в качестве анализатора, Малюс наблюдал ослабление, а иногда и полное исчезновение одного из изображений Солнца. Причиной этого эффекта является полная поляризация света, отраженного от поверхности диэлектрика (в частности, оконного стекла) под углом Брюстера. Именно такой свет может быть полностью погашен анализатором, что и наблюдал Малюс[25].

Отражение света от границы раздела двух диэлектриков, как известно, описывается формулами Френеля

R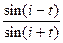_^ = - , (1)

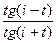R_|| = , (2)

где 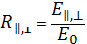- коэффициенты отражения света (по амплитуде), поляризованного в плоскости и перпендикулярно плоскости падения соответственно, i и t - углы падения и преломления. Из формулы (2) следует, что если

i + t = p/2, (3)

то R_|| = 0, т. е. свет, поляризованный в плоскости падения, не отражается. Для света, поляризованного перпендикулярно плоскости падения, отражение имеет место при любом угле падения. При условии (3) закон Снеллиуса n₁×sin i = n₂×sin t запишется в виде

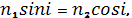(4)

откуда сразу следует закон Брюстера

tg i_Бр = n₂/n₁. (5)

Формула (5) определяет угол Брюстера i_Бр, т. е. такой угол падения, при котором свет, поляризованный в плоскости падения, не отражается вовсе.

Качественно объяснить физическую природу рассмотренного эффекта можно, если считать, что отраженный и преломленный световые пучки образуются в результате переизлучения света молекулами диэлектрика, от поверхности которого происходит отражение. Действительно, если падающий свет поляризован в плоскости падения, то он возбуждает колебания молекул в направлении, перпендикулярном направлению распространения преломленной волны (рис. 8.56). Именно эти колебания и должны сформировать отраженную волну. Но при падении под углом Брюстера отраженная и преломленная волны образуют прямой угол, а, как известно, колеблющийся электрический диполь не излучает в направлении своей оси. Поэтому в этом случае нет отраженной волны. Если же свет поляризован перпендикулярно плоскости падения, то, несмотря на условие (3), колебания молекул диэлектрика формируют отраженную волну, так как диаграмма направленности излучения электрического диполя в этом направлении максимальна.

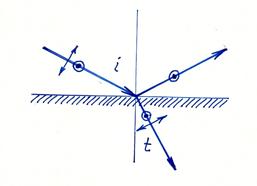Рис. 8.56. Брюстеровское отражение (схема)

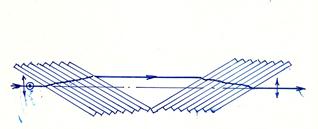Рис. 8.57. Стопа брюстеровских пластинок (стопа Столетова)

При отражении от границы раздела воздух-диэлектрик можно считать n₁ = 1. Рассчитанные по формуле (5) значения i_Бр для разных диэлектриков приведены в таблице.

Диэлектрик	n2	iБр, град
Вода	1,33	53,06
Стекло	1,51	56,48
Алмаз	2.42	67,55

Рассказывая об угле Брюстера, нельзя не остановиться на его применении в поляризационной технике. Брюстеровское отражение является самым простым и дешевым способом получения полностью линейно поляризованного света. В определенных диапазонах длин волн этот способ вообще является единственным. Однако использование отраженного луча в таких поляризаторах не всегда удобно, так как обычно нужно не только получить свет с высокой степенью поляризации, но и иметь возможность изменять азимут поляризации в процессе того или иного эксперимента. А так как направление поляризации отраженного луча определяется плоскостью отражающей поверхности, то, чтобы изменить это направление, надо поворачивать саму плоскость. При этом направление распространения отраженного луча в пространстве изменяется, сбивая настройку экспериментальной установки.

Гораздо удобнее использовать не отраженный, а преломленный луч. После многократного преломления на последовательно расположенных поверхностях раздела диэлектриков, прошедший эту систему луч становится линейно поляризованным в плоскости падения, и при большом числе поверхностей степень поляризации приближается к 100%. Такие устройства (иногда называемые стопами А. Г. Столетова) делаются таким образом, чтобы смещение луча при прохождении половины пластинок компенсировалось обратным смещением этого луча при прохождении остальных пластинок. Тогда стопу можно поворачивать вокруг оси, изменяя азимут поляризации прошедшего луча, а направление распространения этого луча при этом будет оставаться неизменным.

Действующая модель стопы Столетова показана на рис. 8.58. Эта стопа, состоящая из 16 брюстеровских пластинок, является очень хорошим поляризатором для прошедшего света. В этом легко убедиться, если направить на стопу луч поляризованного света (например, от гелий-неонового лазера) и, поворачивая стопу, наблюдать периодическое гашение светового пятна на экране или на стенке.

Рис. 7-58. Стопа Столетова.

Для демонстрации особенностей отражения под углом Брюстера лучше всего попытаться воспроизвести то, что наблюдал Малюс и о чем говорилось в начале этого параграфа. На темном (лучше черном) фоне размещаем кусок стекла, на который кладем какой-либо предмет так, чтобы хорошо был виден и сам предмет, и его изображение в стекле (рис. 8.59а). Затем берем пленочный поляроид и смотрим через него на предмет под углом ~ 30⁰ к поверхности стекла. Вращая поляроид, убеждаемся, что при каком-то положении поляроида отражение предмета в стекле практически полностью исчезает (рис. 8.59б). Если же смотреть под большим или под меньшим углами, то отражение остается при вращении поляроида.

а	б

Рис. 8.59. Исчезновение отражения часов при наблюдении через поляроид.

То же самое можно проделать с отражением предмета в воде. В этом случае отражение предмета не двоится, как при отражении в тонком стекле.

В небольших аудиториях с этим экспериментом студенты могут познакомиться индивидуально. В больших аудиториях следует воспользоваться видеокамерой.

Дата добавления: 2014-01-04