Банковское дисконтирование (учет) по сложной учетной ставке

В практике учетных операций иногда применяют сложную учетную ставку. В этих случаях каждый раз учетная ставка применяется не к первоначальной сумме как при простой учетной ставке, а к сумме, уже дисконтированной на предыдущем этапе.

Пусть долговое обязательство на сумму 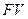со сроком погашения через 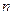лет учитывается раньше срока по сложной годовой ставке .

Если учет осуществляется за год до срока, то начисляются проценты в сумме 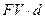. В этом случае владелец векселя получит сумму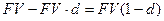

Если учет долгового обязательства осуществляется за два года до срока погашения, то за второй год проценты начисляются уже на сумму 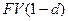, дисконтированную на первом этапе. Тогда владелец векселя получит сумму, равную: 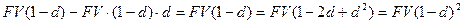и т.д.

Если долговое обязательство продается за 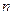лет до срока, то владелец векселя получит сумму .

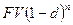Таким образом, дисконтирование по сложной учетной ставке осуществляется по формуле:

где -сложная годовая учетная ставка. (3.11) Здесь 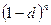- дисконтный множитель. Дисконт равен величине:

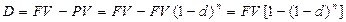
Если дисконтирование производится по учетной ставке 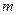раз в году, то применяется формула:

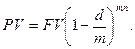(3.12)

Пример. Ценная бумага на сумму 500 000 рублей, учтена за 3 года до срока погашения по сложной учетной ставке 15% годовых. Какова сумма дисконта?

Решение: получит при учете ценной бумаги ее владелец.

Дисконт составит: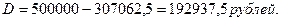

Пример. В условиях предыдущего примера рассчитать сумму, которую получит владелец ценной бумаги при поквартальном дисконтировании.

Решение:

Сравнение результатов свидетельствует о том, что для банка более частое дисконтирование не выгодно, так как при этом увеличивается сумма, выдаваемая владельцу ценной бумаги при ее досрочном учете.

Сравнивая между собой банковское дисконтирование по простой и сложной учетным ставкам, получим следующее:

а) при 0<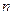<1 справедливо неравенство >;

б) при 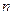>1 неравенство <;

в) при 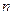=1 значения дисконтных множителей совпадают: =;

Таким образом, при 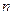<1 результаты финансовой операции для банка выгоднее с применением учета по сложным процентам, так как в этом случае дисконтный множитель будет меньше, чем в случае применения простых процентов, и, следовательно, величина выдаваемой суммы будет меньше. Если же 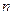>1,то для него выгоднее применить учет по простой учетной ставке.

Дата добавления: 2014-01-04