Расчет средней процентной ставки

Пример

Пример

Пример

Ссуда в размере 2,5 млн. рублей выдана под простые проценты на 2 года, с условием возвратить в конце срока 3,5 млн. руб. Определить доходность этой операции на основе простой и сложной процентных ставок.

Решение: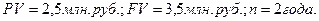

или 20%.

или 18,3%.

На вклад, помещенный в банк под 16% годовых, проценты начисляются ежеквартально. Оцените доходность этой операции на основе эффективной процентной ставки.

Решение: i=0,16; m=4.

В некоторых финансовых операциях общий доход может исчисляться как результат сложения доходов от разных источников. Так, банки кроме взимания процентной ставки за кредит часто устанавливают комиссионное вознаграждение за осуществление операций по расчетным счетам клиентов а также удерживают с клиента определенную сумму, покрывающую затраты банка по каждой операции.

Следовательно, измерение доходности любой финансовой операции сводится к учету всех источников дохода, нахождению суммарного дохода за определенный период времени и сопоставлению его с затратами. Для кредитных операций – это сумма денег, предоставленная в кредит. Для владельца ценных бумаг – это сумма, затраченная для их приобретения. При этом все выплаты должны быть приведены к одному моменту времени, чаще всего к сроку начала или окончания финансовой операции.

Таким образом, в общем случае оценка доходности сводится к определению расчетной процентной ставки, отражающей общую доходность на вложенный капитал.

Ссуда 100 тыс. рублей выдана на 240 дней под 12% годовых. Проценты простые обыкновенные. При выдаче ссуды удержаны комиссионные в размере 1тыс. рублей. Определить полную доходность финансовой операции в виде сложной процентной ставки.

Решение: PV=100 тыс. руб.; t = 240 дней; Y = 360 дней.

Сумма долга с процентами составит:

Затраты составили 99 тыс. руб. (100-1). Срок финансовой операции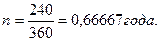

Определим полную доходность финансовой операции в виде сложной процентной ставки из равенства: .

Следовательно, полная доходность этой финансовой операции составляет 13,94%.

В условиях нестабильности финансового рынка процентные ставки могут быть непостоянны во времени. В связи с этим возникает задача определения такого значения процентной ставки, которое определяло бы уровень доходности за весь период финансовой операции. Для решения этой задачи определяют среднюю процентную ставку с помощью уравнения эквивалентности, которое ставит в соответствие коэффициенту наращения, определенному на основе годовой процентной ставки последовательность коэффициентов наращения, задающих схему проведения данной финансовой операции.

а) Предположим, что в течение периода времени 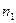установлена ставка простых процентов 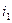, в течение периода времени 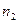действует ставка простых процентов 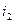и т.д. Всего число периодов начисления процентов -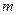. В этом случае срок финансовой операции определяется суммой: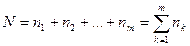

Обозначим процентную ставку ссудных процентов, характеризующую среднюю доходность за конверсионный период, символом 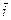. Тогда уравнение эквивалентности для ее определения будет иметь вид:

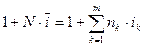
Отсюда

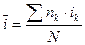(5.4)

Аналогично для простых учетных ставок их средняя определяется из равенства: 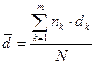. (5.5)

Средняя ставка 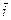(равно как и ) — это взвешенная средняя арифметическая величина, при расчете которой каждому значению процентной ставки ставится в соответствие интервал, в течение которого данное значение ставки использовалось.

В общем виде определение средней ставки может быть сформулировано следующим образом.

Средняя процентная ставка — это ставка, дающая такое наращение, которое эквивалентно наращению с применением ряда разных по значению процентных ставок, применяемых на различных интервалах времени.

Пример. На долг в 400 000 рублей согласно контракту предусматривается начислить годовые простые точные проценты по схеме, определенной следующей таблицей.

Таблица

Период
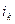
	0,12	0,75	0,09
	0,11	2,0	0,22
	0,08	1,25	0,1
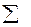
		4,0	0,41

Требуется оценить доходность этой кредитной операции в виде простой годовой процентной ставки и найти сумму долга с процентами.

Решение:

Срок финансовой операции:

Средняя процентная ставка:

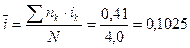
или 10,25 % годовых.

Сумма долга с процентами:

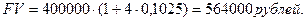
б) Допустим, что доходность операции с плавающей процентной ставкой на каждом интервале начисления была выражена через сложный процент. В этом случае средняя процентная ставка, которая равноценна последовательности ставок за весь период финансовой операции, может быть получена из следующего уравнения эквивалентности: .

Отсюда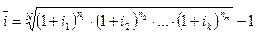, (5.6)

где

.

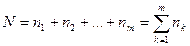Следовательно, сложная средняя процентная ставка рассчитывается по формуле средней геометрической взвешенной.

Пример. Сложная процентная ставка по ссуде определена на уровне 8,5 % плюс маржа 0,5 % в первые 2 года и 0,75 % в последующие 3 года. Требуется определить среднюю ставку сложных процентов.

Решение:

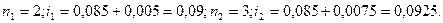
Срок финансовой операции:

Средняя ставка сложных процентов: или 9,15% годовых.

Дата добавления: 2014-01-04